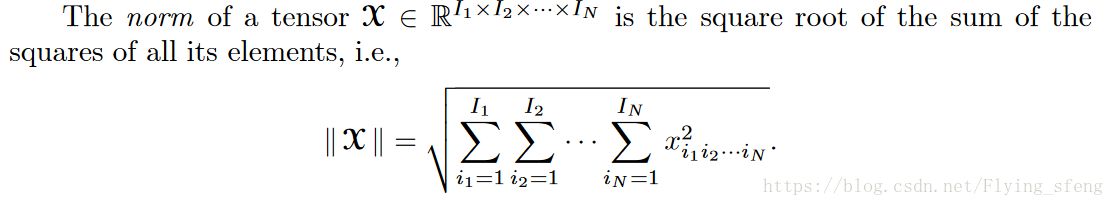轉:張量分解(一):基礎知識
阿新 • • 發佈:2018-12-15
[原地址]https://blog.csdn.net/Flying_sfeng/article/details/80817904
前段時間在組裡分享了張量分解相關的知識,現在想把它整理成一個系列,供有需要的同學閱讀。
下文根據Tensor Decompositions and Applications∗ 整理,原文比較長,我主要整理了一些比較常用的,有需要的同學可以直接閱讀原文。
我們知道,一維的陣列叫向量,二維的叫矩陣,三維及三維以上的就是張量了。
如下圖,就是一個三階張量:

以下為一些張量相關的基礎知識:
1)張量的範數:所有元素的平方和的平方根(類似於矩陣的F範數)
2)張量內積:兩個相同大小的張量的內積為它們對應元素的乘積之和
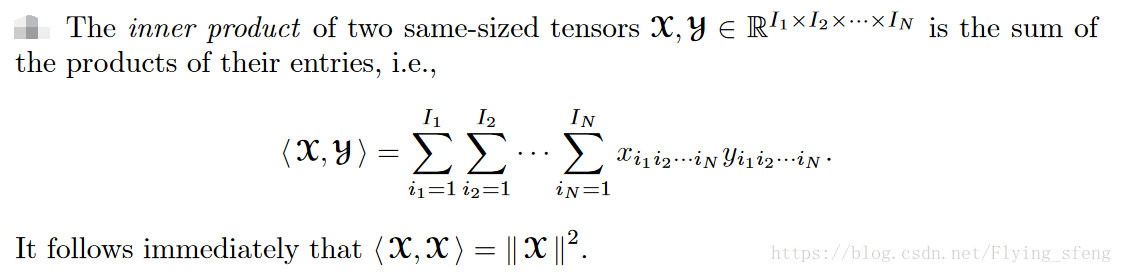
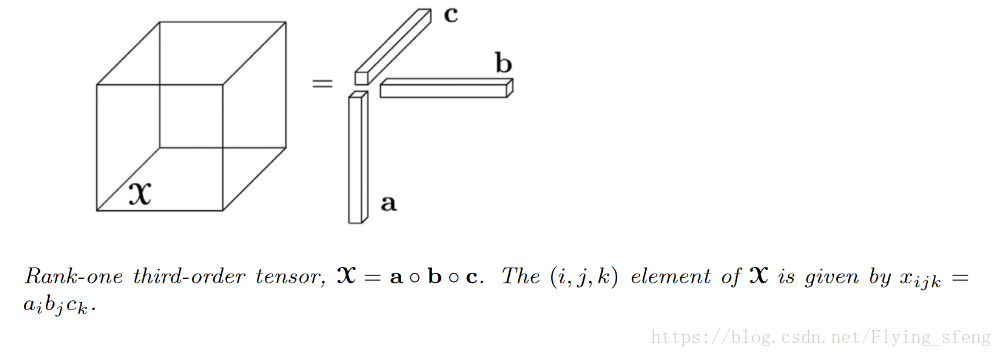
3)Rank-one tensors:一種特殊的張量型別,如果一個N階的張量能以N個向量的外積來表示,那麼這就是一個Rank-one tensors,具體如下圖:

4)Diagonal tensors:

5)張量乘法:
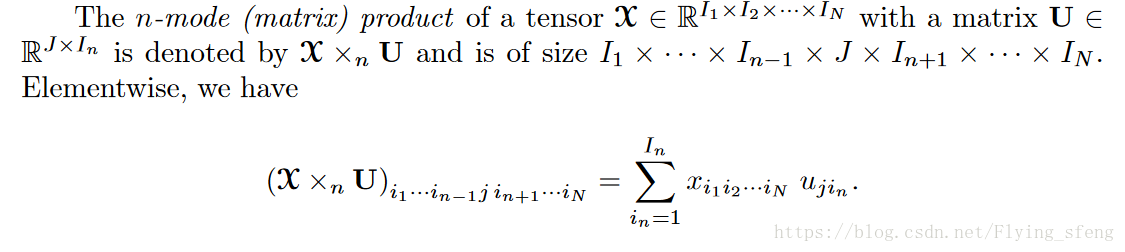
6)Kronecker product:
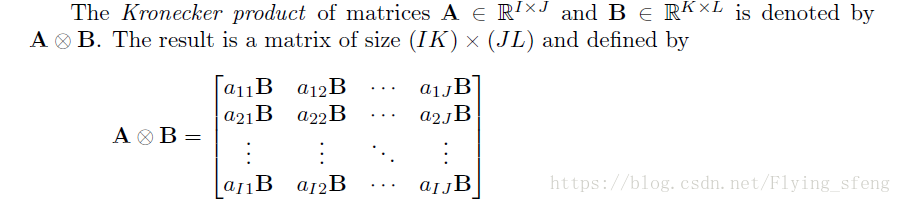
7)Khatri-Rao product:其實就是Kronecker product列元素上的匹配:

8)Hadamard product:按元素相乘,因此兩個tensor的維度必須相同:

以上,便是張量分解領域部分比較常見的知識點,下一篇文章,我將講解一個常見的張量分解演算法:CP decomposition.