二叉堆與堆排序
阿新 • • 發佈:2018-12-15
二叉堆的定義
二叉堆是完全二叉樹或者是近似完全二叉樹。
二叉堆滿足二個特性:
1.父結點的鍵值總是大於或等於(小於或等於)任何一個子節點的鍵值。
2.每個結點的左子樹和右子樹都是一個二叉堆(都是最大堆或最小堆)。
當父結點的鍵值總是大於或等於任何一個子節點的鍵值時為最大堆。當父結點的鍵值總是小於或等於任何一個子節點的鍵值時為最小堆。下圖展示一個最小堆:
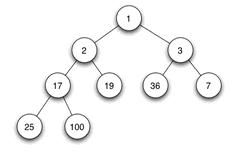
由於其它幾種堆(二項式堆,斐波納契堆等)用的較少,一般將二叉堆就簡稱為堆。
堆的儲存
一般都用陣列來表示堆,i結點的父結點下標就為(i – 1) / 2。它的左右子結點下標分別為2 * i + 1和2 * i + 2。如第0個結點左右子結點下標分別為1和2。
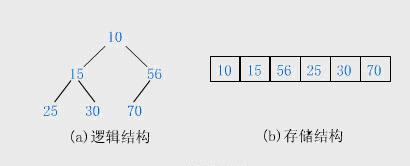
堆的插入
每次插入都是將新資料放在陣列最後。可以發現從這個新資料的父結點到根結點必然為一個有序的數列,現在的任務是將這個新資料插入到這個有序資料中——這就類似於直接插入排序中將一個數據併入到有序區間中
// 新加入i結點 其父結點為(i - 1) / 2 void MinHeapFixup(int a[], int i) { int j, temp; temp = a[i]; j = (i - 1) / 2; //父結點 while (j >= 0 && i != 0) { if (a[j] <= temp) break; a[i] = a[j]; //把較大的子結點往下移動,替換它的子結點 i = j; j = (i - 1) / 2; } a[i] = temp; }
更簡短的表達為:
void MinHeapFixup(int a[], int i)
{
for (int j = (i - 1) / 2; (j >= 0 && i != 0)&& a[i] > a[j]; i = j, j = (i - 1) / 2)
Swap(a[i], a[j]);
}
插入時:
//在最小堆中加入新的資料nNum
void MinHeapAddNumber(int a[], int n, int nNum)
{
a[n] = nNum;
MinHeapFixup(a, n);
}
堆的刪除(自上而下調整堆,自下而上更簡單一些)
按定義,堆中每次都只能刪除第0個數據。為了便於重建堆,實際的操作是將最後一個數據的值賦給根結點,然後再從根結點開始進行一次從上向下的調整。調整時先在左右兒子結點中找最小的,如果父結點比這個最小的子結點還小說明不需要調整了,反之將父結點和它交換後再考慮後面的結點。相當於從根結點將一個數據的“下沉”過程。下面給出程式碼:
// 從i節點開始調整,n為節點總數 從0開始計算 i節點的子節點為 2*i+1, 2*i+2
// 自上而下調整推,以下方法沒有驗證,不一定正確。
void MinHeapFixdown(int a[], int i, int n)
{
int j, temp;
temp = a[i];
j = 2 * i + 1;
while (j < n) //下沉過程
{
if (j + 1 < n && a[j + 1] < a[j]) //在左右孩子中找最小的
j++;
if (a[j] >= temp)
break;
a[i] = a[j]; //把較小的子結點往上移動,替換它的父結點
i = j;
j = 2 * i + 1;
}
a[i] = temp;
}
//在最小堆中刪除數
void MinHeapDeleteNumber(int a[], int n)
{
Swap(a[0], a[n - 1]);
MinHeapFixdown(a, 0, n - 1);
}
堆化陣列

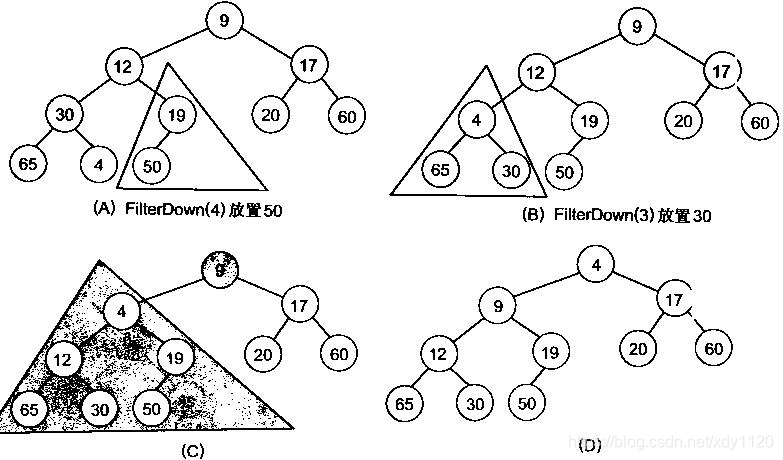
堆排序
首先可以看到堆建好之後堆中第0個數據是堆中最小的資料。取出這個資料再執行下堆的堆化(調整)操作。這樣堆中第0個數據又是堆中最小的資料,重複上述步驟直至堆中只有一個數據時就直接取出這個資料。
