受限玻爾茲曼機(RBM)原理分析以及在Tensorflow的實現
簡介
受限玻爾茲曼機是一種無監督,重構原始資料的一個簡單的神經網路。 受限玻爾茲曼機先把輸入轉為可以表示它們的一系列輸出;這些輸出可以反向重構這些輸入。通過前向和後向訓練,訓練好的網路能夠提取出輸入中最重要的特徵。
為什麼RBM很重要?
因為它能夠自動地從輸入中提取重要的特徵。
RBM有什麼用
用於協同過濾(Collaborative Filtering) 降維(dimensionality reduction) 分類(classification) 特徵學習(feature leatning) 主題模型(topic modeling) 搭建深度置信網路(Deep belief network)
RBM是生成模型嗎?
生成模型和判別模型的區別
判別模型: 考慮一個分類問題,如我們想根據車的一些特徵分辨一輛轎車和一輛SUV。給定一個訓練集,一個演算法如邏輯迴歸,它嘗試找到一條可以直線,以這條直線作為決策邊界把轎車和SUV區分開。 生成模型: 根據汽車,我們可以建立一個模型,比如轎車是什麼樣子的;然後再根據SUV, 我們建立另外一個SUV的模型;最後根據這個兩個模型,判斷一輛車是轎車還是SUV.
生成模型在輸入特徵下有特定的概率分佈。 生成模型中既可以使用監督學習和無監督: 在無監督學習中, 我們想要得到一個P(x)的模型, x是輸入向量; 在監督學習中,我們首先得到的是P(x|y), y是x的標記。舉個例子,如果y標記一輛車是轎車(0)或者SUV(1), 那麼p(x|y=0)就描述了轎車的特徵是怎麼分佈的,p(x|y=1)就描述了轎車的特徵是怎麼分佈的。 如果我們能夠找到P(x|y)和P(y), 我們就能夠使用貝葉斯公式去估算P(y|x),因為P(y|x) = P(x|y)P(y)/P(x).
使用MINST 資料集展示如何使用RBMs
初始化並載入資料
import tensorflow as tf
import numpy as np
from tensorflow.examples.tutorials.mnist import input_data
#!pip install pillow
from PIL import Image
#import Image
from utils import tile_raster_images
import matplotlib.pyplot as plt
%matplotlib inlinemnist = input_data.read_data_sets("MNIST_data/", one_hot=True) trX, trY, teX, teY = mnist.train.images, mnist.train.labels, mnist.test.images, mnist.test.labels
RBM的層
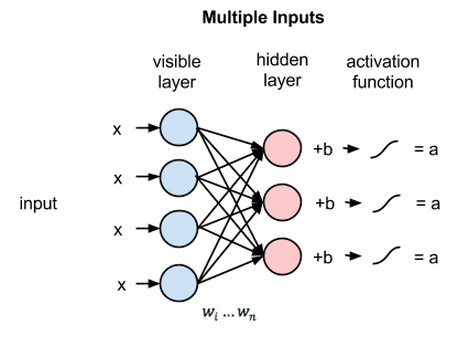
一個RBM有兩個層,第一層叫可視層(visible)或者輸入層,第二層是隱藏層( hidden layer)。MNIST資料庫的每一張圖片有784個畫素,所以可視層必須有784個輸入節點。第二個隱藏層在這裡設為ii個神經元。每一個神經元是2態的(binary state), 稱為si。根據jj個輸入單元,並由邏輯函式(logistic function) 產生一個概率輸出,決定每一個隱藏層的單元是開(si = 1)是還關(si =0)。 這裡我們取 i=500i=500.
第一層的每一個節點有一個偏差 (bias),使用vb表示; 第二層的每一個節點也有一個偏差,使用hb表示;
vb = tf.placeholder("float", [784])
hb = tf.placeholder("float", [500])定義可視層和隱藏層之間的權重,行表示輸入節點,列表示輸出節點,這裡權重W是一個784x500的矩陣。
W = tf.placeholder("float", [784, 500])訓練好RBM能做什麼
當RBM被訓練好了,它就能夠在跟定一些隱藏值(如下雨)來計算一個事件(比如溼滑路面)的概率. 那就是說,RBM可以被看作是生成模型,它給每一個可能的二態向量( binary states vectors)生成一個概率。 這些二態向量( binary states vectors)多少種情況? 可視層可以有不同的二態(0或1),或者說有不同的設定。比如,當輸入層只有7個單元時,它有2727 中排列,每一種排列有它對應的概率(這裡我們假設沒有偏差) - (0,0,0,0,0,0,0) –> p(config1)=p(v1)=p(s1=0,s2=0, .., s7=0) - (0,0,0,0,0,0,1) –> p(config2)=p(v2)=p(s1=0,s2=1, .., s7=1) - (0,0,0,0,0,1,0) –> p(config3)=p(v3)=p(s1=1,s2=0, .., s7=0) - (0,0,0,0,0,1,1) –> p(config4)=p(v4)=p(s1=1,s2=1, .., s7=1) - etc. 所以, 如果我們有784個單元,對於全部的27842784種輸入情況,它會產生一個概率分佈,P(v)。
如何訓練RBM
訓練分為兩個階段:1) 前向(forward pass) 2)後向( backward pass)或者重構(reconstruction):
階段1
前向:改變的是隱藏層的值。 輸入資料經過輸入層的所有節點傳遞到隱藏層。這個計算是隨機開始(This computation begins by making stochastic decisions about whether to transmit that input or not (i.e. to determine the state of each hidden layer)). 在隱藏層的節點上,X乘以W再加上h_bias. 這個結果再通過sigmoid函式產生節點的輸出或者狀態。因此,每個隱藏節點將有一個概率輸出。對於訓練集的每一行,生成一個概率構成的張量(tensor),這個張量的大小為[1X500], 總共55000個向量[h0=55000x500]。 接著我們得到了概率的張量,從所有的分佈中取樣,h0。 那就是說,我們從隱藏層的概率分佈中取樣啟用向量(activation vector). 這些得到的樣本用來估算反向梯度(negative phase gradient).
X = tf.placeholder("float", [None, 784])
_h0= tf.nn.sigmoid(tf.matmul(X, W) + hb) #probabilities of the hidden units
h0 = tf.nn.relu(tf.sign(_h0 - tf.random_uniform(tf.shape(_h0)))) #sample_h_given_X參考下面的程式碼理解上面的程式碼:
with tf.Session() as sess:
a= tf.constant([0.7, 0.1, 0.8, 0.2])
print sess.run(a)
b=sess.run(tf.random_uniform(tf.shape(a)))
print b
print sess.run(a-b)
print sess.run(tf.sign( a - b))
print sess.run(tf.nn.relu(tf.sign( a - b)))
[0.7 0.1 0.8 0.2]
[0.31160402 0.3776673 0.42522812 0.8557215 ]
[ 0.38839597 -0.2776673 0.3747719 -0.6557215 ]
[ 1. -1. 1. -1.]
[1. 0. 1. 0.]階段2
反向(重構): RBM在可視層和隱藏層之間通過多次前向後向傳播重構資料。 所以在這個階段,從隱藏層(h0)取樣得到的啟用向量作為輸入。相同的權重矩陣和可視層偏差將用於計算並通過sigmoid函式。其輸出是一個重構的結果,它近似原始輸入。
_v1 = tf.nn.sigmoid(tf.matmul(h0, tf.transpose(W)) + vb)
v1 = tf.nn.relu(tf.sign(_v1 - tf.random_uniform(tf.shape(_v1)))) #sample_v_given_h
h1 = tf.nn.sigmoid(tf.matmul(v1, W) + hb)重構步驟
- 從資料集中拿一個數據, 如x, 把它通過網路
- Pass 0: (x) -> (x:-:_h0) -> (h0:-:v1) (v1 is reconstruction of the first pass)
- Pass 1: (v1) -> (v1:-:h1) -> (_h0:-:v2) (v2 is reconstruction of the second pass)
- Pass 2: (v2) -> (v2:-:h2) -> (_h1:-:v3) (v3 is reconstruction of the third pass)
- Pass n: (vn) -> (vn:-:hn+1) -> (_hn:-:vn+1)(vn is reconstruction of the nth pass)
如何計算梯度
為了訓練RBM, 我們必須使賦值到訓練集V上的概率乘積最大。假如資料集V,它的每一行看做是一個可視的向量v:

或者等效地最大化訓練集概率的對數

我們也可以定義一個目標函式並嘗試最小化它。為了實現這個想法,我們需要這個函式的各個引數的偏導數。從上面的表示式我們知道,他們都是由權重和偏差間接組成的函式,所以最小化目標函式就是優化權重。因此,我們可以使用隨機梯度下降(SGD)去找到最優的權重進而使目標函式取得最小值。在推導的時候,有兩個名詞,正梯度和負梯度。這兩個狀態反映了他們對模型概率密度的影響。正梯度取決於觀測值(X),負梯度只取決於模型。
正的階段增加訓練資料的可能性; 負的階段減少由模型生成的樣本的概率。
負的階段很難計算,所以我們用一個對比散度(Contrastive Divergence (CD))去近似它。它是按照這樣的方式去設計的:梯度估計的方向至少有一些準確。實際應用中,更高準確度的方法如CD-k 或者PCD用來訓練RBMs。 計算對比散度的過程中,我們要用吉布斯取樣(Gibbs sampling)對模型的分佈進行取樣。
對比散度實際是一個用來計算和調整權重矩陣的一個矩陣。 改變權重W漸漸地變成了權重值的訓練。然後在每一步(epoch), W通過下面的公式被更新為一個新的值w’。
W′=W+α∗CDW′=W+α∗CD
αα 是很小的步長,也就是大家所熟悉的學習率(Learning rate)
如何計算相對散度?
下面展示了單步相對散度的計算(CD-1)步驟: 1. 從訓練集X中取訓練樣本,計算隱藏層的每個單元的概率並從這個概率分佈中取樣得到一個隱藏層啟用向量h0;
_h0=sigmoid(X⊗W+hb)_h0=sigmoid(X⊗W+hb) h0=sampleProb(_h0)h0=sampleProb(_h0)
2. 計算X和h0的外積,這就是正梯度
w_pos_grad=X⊗h0w_pos_grad=X⊗h0 (Reconstruction in the first pass)
3. 從h重構v1, 接著對可視層單元取樣,然後從這些取樣得到的樣本中重取樣得到隱藏層啟用向量h1.這就是吉布斯取樣。
_v1=sigmoid(h0⊗transpose(W)+vb)_v1=sigmoid(h0⊗transpose(W)+vb) v1=sampleprob(_v1)v1=sampleprob(_v1)(Sample v given h) h1=sigmoid(v1⊗W+hb)h1=sigmoid(v1⊗W+hb)
4. 計算v1和h1的外積,這就是負梯度。
w_neg_grad=v1⊗h1w_neg_grad=v1⊗h1(Reconstruction 1)
5. 對比散度等於正梯度減去負梯度,對比散度矩陣的大小為784x500.
CD=(w_pos_grad−w_neg_grad)/datapointsCD=(w_pos_grad−w_neg_grad)/datapoints
7. 更新權重為W′=W+α∗CDW′=W+α∗CD 8. 最後可視層節點會儲存取樣的值。
什麼是取樣(sampleProb)?
在前向演算法中,我們隨機地設定每個hi的值為1,伴隨著概率sigmoid(v⊗W+hb)sigmoid(v⊗W+hb); 在重構過程中,我們隨機地設定每一個vi的值為1,伴隨著概率sigmoid(h⊗transpose(W)+vb)sigmoid(h⊗transpose(W)+vb)
alpha = 1.0
w_pos_grad = tf.matmul(tf.transpose(X), h0)
w_neg_grad = tf.matmul(tf.transpose(v1), h1)
CD = (w_pos_grad - w_neg_grad) / tf.to_float(tf.shape(X)[0])
update_w = W + alpha * CD
update_vb = vb + alpha * tf.reduce_mean(X - v1, 0)
update_hb = hb + alpha * tf.reduce_mean(h0 - h1, 0)什麼是目標函式?
目的:最大限度地提高我們從該分佈中獲取資料的可能性 計算誤差: 每一步(epoch), 我們計算從第1步到第n步的平方誤差的和,這顯示了資料和重構資料的誤差。
err = tf.reduce_mean(tf.square(X - v1))
# tf.reduce_mean computes the mean of elements across dimensions of a tensor.
建立一個回話並初始化向量:
cur_w = np.zeros([784, 500], np.float32)
cur_vb = np.zeros([784], np.float32)
cur_hb = np.zeros([500], np.float32)
prv_w = np.zeros([784, 500], np.float32)
prv_vb = np.zeros([784], np.float32)
prv_hb = np.zeros([500], np.float32)
sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)檢視第一次執行的誤差:
sess.run(err, feed_dict={X: trX, W: prv_w, vb: prv_vb, hb: prv_hb})
# 0.48134533整個演算法的運算流程:
對於每一個epoch:
對於每一batch:
計算對比散度:
對batch中的每一個數據點:
w_pos_grad = 0, w_neg_grad= 0 (matrices)
資料向前傳播,計算v(重構)和h
更新w_neg_grad = w_neg_grad + v1 ⊗ h1
對比散度=pos_grad和neg_grad的平均值除以輸入資料個數
更新權重和偏差 W' = W + alpha * CD
計算誤差
重複下一epoch直到誤差足夠小或者在多個epoch下不再改變
#Parameters
epochs = 5
batchsize = 100
weights = []
errors = []
for epoch in range(epochs):
for start, end in zip( range(0, len(trX), batchsize), range(batchsize, len(trX), batchsize)):
batch = trX[start:end]
cur_w = sess.run(update_w, feed_dict={ X: batch, W: prv_w, vb: prv_vb, hb: prv_hb})
cur_vb = sess.run(update_vb, feed_dict={ X: batch, W: prv_w, vb: prv_vb, hb: prv_hb})
cur_hb = sess.run(update_hb, feed_dict={ X: batch, W: prv_w, vb: prv_vb, hb: prv_hb})
prv_w = cur_w
prv_vb = cur_vb
prv_hb = cur_hb
if start % 10000 == 0:
errors.append(sess.run(err, feed_dict={X: trX, W: cur_w, vb: cur_vb, hb: cur_hb}))
weights.append(cur_w)
print 'Epoch: %d' % epoch,'reconstruction error: %f' % errors[-1]
plt.plot(errors)
plt.xlabel("Batch Number")
plt.ylabel("Error")
plt.show()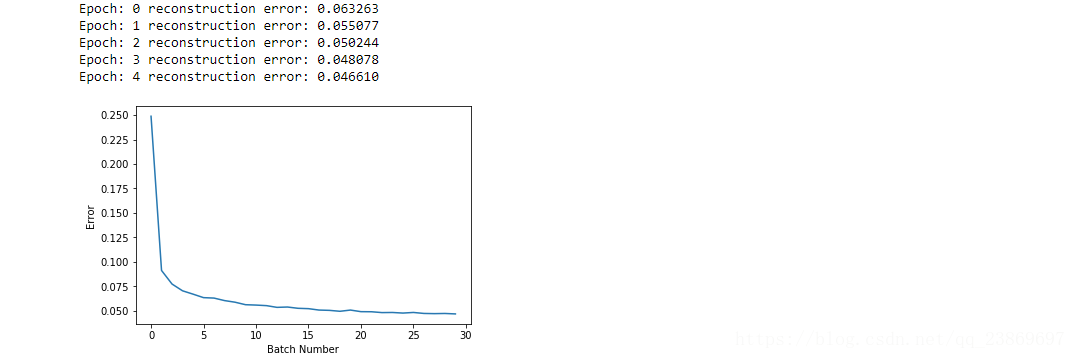
uw = weights[-1].T
print uw # a weight matrix of shape (500,784)我們能夠獲得每一個隱藏的單元並可視化隱藏層和輸入之間的連線。使用tile_raster_images可以幫助我們從權重或者樣本中生成容易理解的圖片。它把784行轉為一個數組(比如25x20),圖片被重塑並像地板一樣鋪開。
tile_raster_images(X=cur_w.T, img_shape=(28, 28), tile_shape=(25, 20), tile_spacing=(1, 1))
import matplotlib.pyplot as plt
from PIL import Image
%matplotlib inline
image = Image.fromarray(tile_raster_images(X=cur_w.T, img_shape=(28, 28) ,tile_shape=(25, 20), tile_spacing=(1, 1)))
### Plot image
plt.rcParams['figure.figsize'] = (18.0, 18.0)
imgplot = plt.imshow(image)
imgplot.set_cmap('gray') 
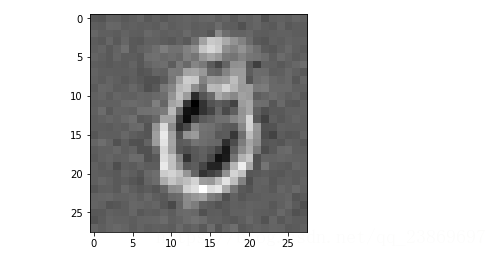
下面觀察其中一個已經訓練好的隱藏層單元的權重,灰色代表權重為0,越白的地方權重越大,接近1.相反得, 越黑的地方,權重越負。 權重為正的畫素使隱藏層單元啟用的概率,負的畫素會減少隱藏層單元被啟用的概率。 所以我們可以知道特定的小塊(隱藏單元) 可以提取特徵如果給它輸入。
我們再看看重構得到一張圖片 1)首先畫出一張原始的圖片
sample_case = trX[1:2]
img = Image.fromarray(tile_raster_images(X=sample_case, img_shape=(28, 28),tile_shape=(1, 1), tile_spacing=(1, 1)))
plt.rcParams['figure.figsize'] = (2.0, 2.0)
imgplot = plt.imshow(img)
imgplot.set_cmap('gray') #you can experiment different colormaps (Greys,winter,autumn)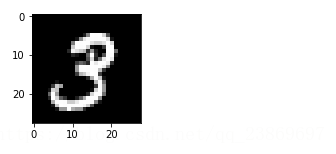
hh0 = tf.nn.sigmoid(tf.matmul(X, W) + hb)
vv1 = tf.nn.sigmoid(tf.matmul(hh0, tf.transpose(W)) + vb)
feed = sess.run(hh0, feed_dict={ X: sample_case, W: prv_w, hb: prv_hb})
rec = sess.run(vv1, feed_dict={ hh0: feed, W: prv_w, vb: prv_vb})3) 畫出重構的圖片
img = Image.fromarray(tile_raster_images(X=rec, img_shape=(28, 28),tile_shape=(1, 1), tile_spacing=(1, 1)))
plt.rcParams['figure.figsize'] = (2.0, 2.0)
imgplot = plt.imshow(img)
imgplot.set_cmap('gray')