曼哈頓距離最小生成樹(樹狀陣列)
POJ-3241 Object Clustering
Dscription
We have N (N ≤ 10000) objects, and wish to classify them into several groups by judgement of their resemblance. To simply the model, each object has 2 indexes a and b (a, b ≤ 500). The resemblance of object i and object j is defined by dij = |ai - aj| + |bi - bj|, and then we say i
Input
The first line contains two integers N and K. The following N lines each contain two integers a and b, which describe a object.
Output
A single line contains the minimum X.
Sample Input
6 2 1 2 2 3 2 2 3 4 4 3 3 1
Sample Output
2
- 題意 -
曼哈頓距離最小生成樹上第k大的邊. 曼哈頓距離: (對於點A(x1, y1), B(x2, y2)) dis(A,B)=|x1−x2|+|y1−y2| dis(A,B)=|x1−x2|+|y1−y2| . (下文中dis() dis() , 距離均指曼哈頓距離) (下文中dis() dis() , 距離均指曼哈頓距離) (下文中dis() dis() , 距離均指曼哈頓距離)
- 思路 -
參考題解: http://blog.csdn.net/huzecong/article/details/8576908
直接暴力的話會有N 2 N2 條邊, 總複雜度O(N 2 logN)(N≤10000) O(N2logN)(N≤10000) .
果斷爆炸.
我們可以刪去一些無用邊.
對於一個平面上的點 i(x i ,y i ) i(xi,yi) , 我們以它為中心把周圍部分為8份.
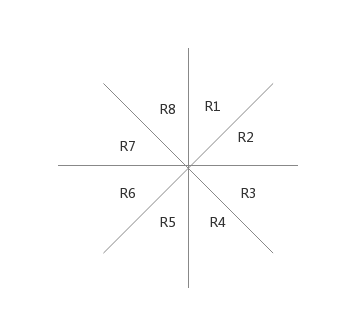 考慮每一份中最多有一個點與點 i 相連, 如 R1:
考慮每一份中最多有一個點與點 i 相連, 如 R1:
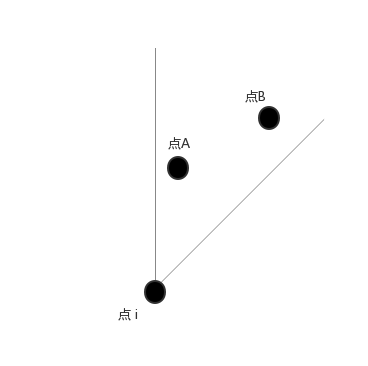 設此時點A是與點 i 距離最小的點, 則為點A, i建一條邊, 考慮該部分的其它點(如點B), 它們與 A 的距離顯然小於與 i 的距離(如dis(A,B)<dis(i,B) dis(A,B)<dis(i,B) ), 所以其它點與 A 連邊優於i.
以上圖三個點為例, 用兩條邊將它們聯通的最小代價W=dis(i,A)+dis(A,B)≤dis(i,A)+dis(i,B) W=dis(i,A)+dis(A,B)≤dis(i,A)+dis(i,B)
dis(i,A)+dis(A,B)=dis(i,A)+dis(i,B) dis(i,A)+dis(A,B)=dis(i,A)+dis(i,B) 的情況如下:(A−B A−B 連線垂直於A−i A−i 連線)
設此時點A是與點 i 距離最小的點, 則為點A, i建一條邊, 考慮該部分的其它點(如點B), 它們與 A 的距離顯然小於與 i 的距離(如dis(A,B)<dis(i,B) dis(A,B)<dis(i,B) ), 所以其它點與 A 連邊優於i.
以上圖三個點為例, 用兩條邊將它們聯通的最小代價W=dis(i,A)+dis(A,B)≤dis(i,A)+dis(i,B) W=dis(i,A)+dis(A,B)≤dis(i,A)+dis(i,B)
dis(i,A)+dis(A,B)=dis(i,A)+dis(i,B) dis(i,A)+dis(A,B)=dis(i,A)+dis(i,B) 的情況如下:(A−B A−B 連線垂直於A−i A−i 連線)
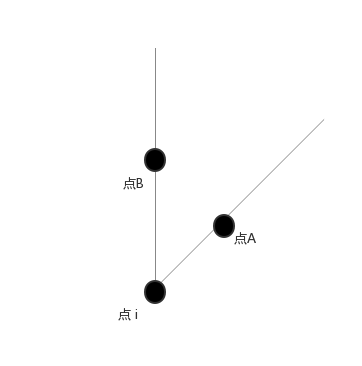 所以對於每個點每一份中只需要連一條邊, 由於邊是無向的, 我們可以只連向右的邊(也就是R1-4內的點, 點 i 向左的連線由左邊的點來連), 這樣就只有N*4條邊了.
繼續分析R1的情況, 如何找到 A 點.
發現首先 R1 區間內的點 k 滿足 :
X i ≤X k Xi≤Xk
X k −X i ≤Y k −Y i Xk−Xi≤Yk−Yi 即 Y i −X i ≤Y k −X k Yi−Xi≤Yk−Xk (k為R1內任一點)
我們在滿足條件的點中找到X+Y X+Y 最小的節點就行了.
於是我們可以維護一個樹狀陣列(線段樹), 底層按離散化後的Y−X Y−X 排序, 維護區間內X+Y X+Y 的最小值,
按照先從右到左, 再從上到下的順序插入節點並查詢.
對於R2-4三個部分, 我們可以對點進行旋轉, 將它們轉換為 R1 內的點.
所以對於每個點每一份中只需要連一條邊, 由於邊是無向的, 我們可以只連向右的邊(也就是R1-4內的點, 點 i 向左的連線由左邊的點來連), 這樣就只有N*4條邊了.
繼續分析R1的情況, 如何找到 A 點.
發現首先 R1 區間內的點 k 滿足 :
X i ≤X k Xi≤Xk
X k −X i ≤Y k −Y i Xk−Xi≤Yk−Yi 即 Y i −X i ≤Y k −X k Yi−Xi≤Yk−Xk (k為R1內任一點)
我們在滿足條件的點中找到X+Y X+Y 最小的節點就行了.
於是我們可以維護一個樹狀陣列(線段樹), 底層按離散化後的Y−X Y−X 排序, 維護區間內X+Y X+Y 的最小值,
按照先從右到左, 再從上到下的順序插入節點並查詢.
對於R2-4三個部分, 我們可以對點進行旋轉, 將它們轉換為 R1 內的點.
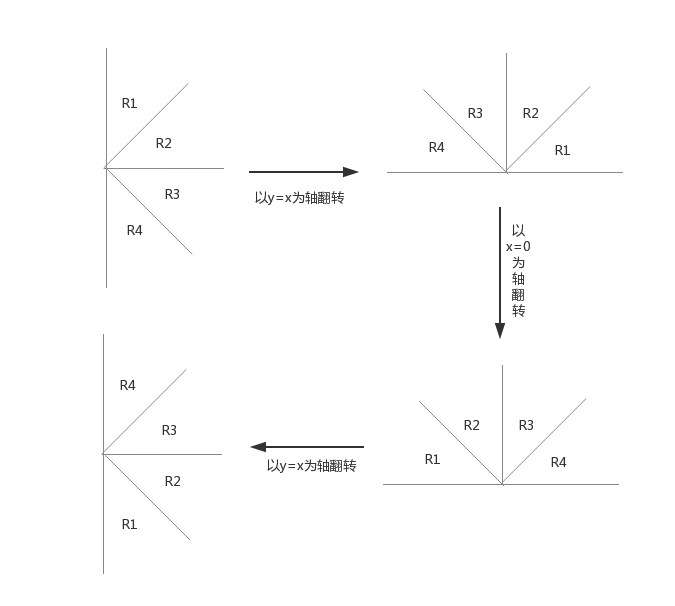 (注意看原先的R1的位置依次有R2, R3, R4的點, 這樣就可以連出四個部分的邊了)
細節見程式碼.
(注意看原先的R1的位置依次有R2, R3, R4的點, 這樣就可以連出四個部分的邊了)
細節見程式碼.
- 程式碼 -
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1e5 + 5;
const int inf = 0x3f3f3f3f;
struct edge
{
int x, y, v;
bool operator < (const edge &tmp) const
{
return v < tmp.v;
}
} E[N<<3];
struct point
{
int x, y, id;
bool operator < (const point &tmp) const
{
return x == tmp.x ? y < tmp.y : x < tmp.x;
}
} P[N];
struct lsh
{
int id, a;
bool operator < (const lsh &tmp) const
{
return a < tmp.a;
/* if (a == tmp.a) return id < tmp.id;
return a < tmp.a;
*/
}
} LSH[N];
int A[N], F[N];
int MI[N], ID[N];
int n, c, sz, tot, cnt;
int lowbit (int x)
{
return x&(-x);
}
int query(int x)
{
int ans = -1, mi = inf;
for (; x <= n; x += lowbit(x))
if (MI[x] < mi)
{
mi = MI[x];
ans = ID[x];
}
return ans;
}
void modify(int x, int mi, int id)
{
for (; x > 0; x -= lowbit(x))
if (MI[x] > mi)
{
MI[x] = mi;
ID[x] = id;
}
}
//BIT維護的是某數字代表的區間的X+Y最小值, 若一區間的不同位置最小值不同, 該區間則沒有最小值(即MI陣列維護的是其表示的區間都可以取到的最小值)
int find(int x)
{
return F[x] == x ? x : F[x] = find(F[x]);
}
void join(int x, int y)
{
int fx = find(x), fy = find(y);
if (fx == fy) return;
F[fx] = fy;
cnt++;
}
void init ()
{
sort(P + 1, P + n + 1);
for (int i = 1; i <= n; ++i)
{
LSH[i].a = P[i].y - P[i].x;
LSH[i].id = i;
MI[i] = inf;
ID[i] = -1;
}
}
int abs(int x, int y)
{
return x > 0 ? x : -x;
}
int dts(int x, int y)
{
return abs(P[x].x - P[y].x) + abs(P[x].y -P[y].y);
}
void add_edge (int x, int y, int d)
{
E[++sz].x = x;
E[sz].y = y;
E[sz].v = d;
}
int main()
{
scanf("%d%d", &n, &c);
for (int i = 1; i <= n; ++i)
{
scanf("%d%d", &P[i].x, &P[i].y);
P[i].id = i;
}
for (int cas = 1; cas <= 4; ++cas)
{
if (cas == 2 || cas == 4)
for (int i = 1; i <= n; ++i)
swap(P[i].x, P[i].y);
if (cas == 3)
for (int i = 1; i <= n; ++i)
P[i].x = -P[i].x;
init();
sort(LSH + 1, LSH + n + 1);//按Y-X離散化
for (int i = 1; i <= n; ++i)
A[LSH[i].id] = i; //A表示某點在BIT中的位置
for (int i = n; i >= 1; --i)
{
int tmp = query(A[i]);
if (tmp != -1)
add_edge(P[tmp].id, P[i].id, dts(tmp, i));
modify(A[i], P[i].x + P[i].y, i);
}
}
for (int i = 1; i <= n; ++i) F[i] = i;
sort(E + 1, E + sz + 1);
for (int i = 1; i <= sz; ++i)
{
join(E[i].x, E[i].y);
if (cnt == n - c)
{
printf("%d\n", E[i].v);
break;
}
}
return 0;
}
