2. 程式人生 > >等額年金法總結

等額年金法總結

阿新 • • 發佈：2018-12-15

今天企業管理這門課遇到了等額年金法(等額年金在專案服務期內連續、等額發生在各期期末)，，總結一下：

什麼是等額年金法

　　等額年金法指運用年金法，使各期租金均等的租金計算方法。

　　等額年金髮生在(或折算為)某一特定時間序列各計息期末的等額序列。即從計算期的第一年至最後一年年末的效益額都相等時，稱為等額年金。

等額年金法的型別

　　等額年金法分為先付和後付。

　　1）先付租金的等額年金法

　　在租金先付的情況下，等額年金法的計算公式為：

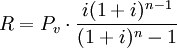
　　R=P_v\cdot\frac{i(1+i)^{n-1}}{(1+i)^n-1}

　　2)後付租金的等額年金法

　　按照年金法計算的基本原理，後付租金的等額年金法的基本計算公式為：

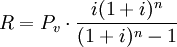
　　R=P_v\cdot\frac{i(1+i)^n}{(1+i)^n-1}

所謂現值是指在將來各個不同時期所支付的每一筆付款或一系列付款所摺合的現金金額與現在支付的付款等值。現值是隨遠期付款的貼現利率變化而變化，如折現率為10％，一年以後的1000元，只相當現在的909.09元，這909.09元即為1000元將來貨幣的現值。現值的計算公式為：

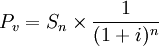
　　P_v=S_n \times \frac{1}{(1+i)^n}

　　其中：P_v為本金(現值)，i為複利率，n為複利次數，Sn為本利和(將來值/終值)

 

等額年金法計算公式的推導

　　1．期末後付租金複利定額年金法公式。根據現值計算公式，設R為每次(相同間隔)應付租金，P_v為租賃物件總成本，i為付租間隔期費率，n為付租次數，則，

　　第一次支付租金的現值為 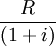\frac{R}{(1+i)}

　　第二次支付租金的現值為 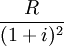\frac{R}{(1+i)^2}

　　......

　　第n-1次支付租金的現值為 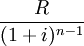\frac{R}{(1+i)^{n-1}}

　　第n次支付租金的現值為 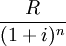\frac{R}{(1+i)^n}

　　第一至第n次支付租金的現值和與租賃資產的概算成本相等，即：

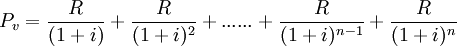　　P_v=\frac{R}{(1+i)} + \frac{R}{(1+i)^2} + ......+ \frac{R}{(1+i)^{n-1}} + \frac{R}{(1+i)^n} ...... ①

　　將上式進行簡化，等式兩邊各乘以(1+i)，則：

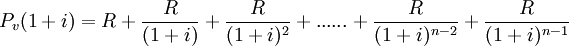　　P_v(1+i)=R + \frac{R}{(1+i)} + \frac{R}{(1+i)^2} + ......+ \frac{R}{(1+i)^{n-2}} + \frac{R}{(1+i)^{n-1}} ...... ②

　　以②-①，則

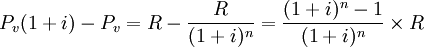
　　P_v(1+i)-P_v=R- \frac{R}{(1+i)^n}= \frac{(1+i)^n-1}{(1+i)^n} \times R

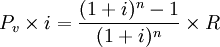
　　P_v \times i=\frac{(1+i)^n-1}{(1+i)^n} \times R

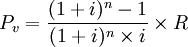
　　P_v=\frac{(1+i)^n-1}{(1+i)^n \times i} \times R

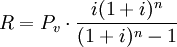
　　R=P_v\cdot\frac{i(1+i)^n}{(1+i)^n-1}

2．有寬限期的期末後付租金複利等額年金法計算公式。有寬限期的期末付租公式。其原理與期末付租基本相同，只是將寬限期的本利和作為實租的總成本。寬限期的本利和為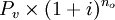：P_v \times (1+i)^{n_o}其中no為寬限期計息次數，所以，有寬限期的期末付租公式為：

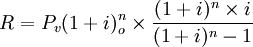
　　R=P_v(1+i)^n_o \times \frac{(1+i)^n \times i}{(1+i)^n - 1}

3，期初先付租金複利定額年金法計算公式。期初付租，第一次付租日即為成交日，那麼，第一次付租額與其現值相等，所以：

　　第一次的現值為R

　　第二次的現值為 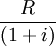\frac{R}{(1+i)}

　　......

　　最後一次的現值為 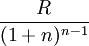\frac{R}{(1+n)^{n-1}}

　　第一次至最後一次支付租金的現值即為租賃資產的概算成本，故：

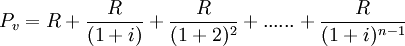　　P_v = R + \frac{R}{(1+i)} + \frac{R}{(1+2)^2} + ......+ \frac{R}{(1+i)^{n-1}} ……①

　　等式兩邊各乘以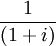\frac{1}{(1+i)}，則：

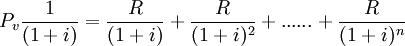　　P_v \frac{1}{(1+i)}=\frac{R}{(1+i)}+\frac{R}{(1+i)^2}+......+\frac{R}{(1+i)^{n}} ...... ②

　　以①-②，則

　　P_v-P_v \frac{1}{(1+i)} = R - \frac{R}{(1+i)^n}

　　P_v[1- \frac{1}{(1+i)}] = \frac{(1+i)^n-1}{(1+i)^n} \times R

　　P_v[\frac{i}{(1+i)}] = \frac{(1+i)^n - 1}{(1+i)^n} \times R

　　P_v= \frac{(1+i)[(1+i)^n-1]}{(1+i)^n \times i} \times R

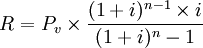
　　R=P_v \times \frac{(1+i)^{n-1} \times i}{(1+i)^n-1}

等額年金法計算應用例項

　　某企業向某租賃機構租用一套裝置，購價95000元，運輸費、保險費，安裝除錯費5000元，租賃期限三年，年租賃費率10％，每季度付租一次，按期末後付、寬限期6個月期末後付和期初先付三種複利年金方法計算租金：

　　已知：P_v＝95000+5000=100000

　　n＝36÷3＝12

　　i=10％÷4＝0.1÷4＝0.025

　　1．用期末後付年金法計算：

　　每期租金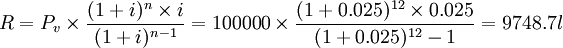R=P_v \times \frac{(1+i)^n \times i}{(1+i)^{n-1}}=100000 \times \frac{(1+0.025)^{12} \times 0.025}{(1+0.025)^{12} - 1}=9748.7l(元)

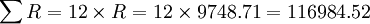　　總租金\sum R=12 \times R = 12 \times 9748.71 = 116984.52(元)

　　2．用期初先付年金法計算：

　　每期租金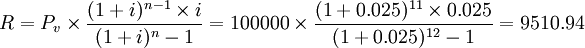R=P_v \times \frac{(1+i)^{n-1} \times i}{(1+i)^n -1} = 100000 \times \frac{(1+0.025)^{11} \times 0.025}{(1+0.025)^{12} - 1}=9510.94(元)

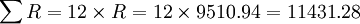　　總租金\sum R = 12 \times R = 12 \times 9510.94 = 11431.28(元)

　　3．用寬限期6個月後付年金法計算：

　　每期租金

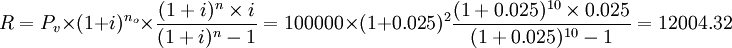　　R = P_v \times (1+i)^{n_o} \times \frac{(1+i)^n \times i}{(1+i)^n - 1}=100000 \times (1+0.025)^2 \frac{(1+0.025)^{10} \times 0.025}{(1+0.025)^{10} - 1}=12004.32(元)

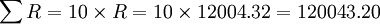　　總租金 \sum R = 10 \times R = 10 \times 12004.32=120043.20(元)

參考連結:https://wiki.mbalib.com/wiki/等額年金法

參考連結：https://wenku.baidu.com/view/4c338472aaea998fcd220e3a.html 

 

 

 

 

相關推薦

等額年金法總結

今天企業管理這門課遇到了等額年金法(等額年金在專案服務期內連續、等額發生在各期期末)，，總結一下： 什麼是等額年金法 　　等額年金法指運用年金法，使各期租金均等的租金計算方法。 　　等額年金髮生在(或折算為)某一特定時間序列各計息期末的等額序列。即從計算期的第一年至最後一年年末的效

2048遊戲回想二：算法總結（移動、合並、動畫等）

switch com asm isp error 結束 復雜 因此 playsound 假設僅僅是單純的寫一個2048遊戲。讓這個遊戲能夠玩的話，工作量還是蠻小的。只

js高斯消元法解決n元一次方程組--算等額分期

fine 計算 calc 賦值 行合並 change amp block 有效 importClass(java.text.DecimalFormat);let df = new DecimalFormat("0.##"); /*** 增廣矩陣機

幾種基本排序算法總結

子序列 system aop 大於等於 != pri i++ index 元素移動 以下均采用從小到大排序： 1.選擇排序算法 個人覺得選擇排序算法是容易理解的排序算法，即從n個元素中選擇最小的一個元素與第一個元素交換，再將除第一個元素之外的n-1個元素找到最小的一

查找算法總結(一)—順序、二分、二叉、紅黑

hash 要求 保存 ges 標準 正是 搜索路徑 初始化 返回鍵 1.順序查找 在查找中我們一個一個順序的遍歷表中的所有鍵並使用equals（）方法來查找匹配的鍵。 優點：對數組的結構沒有特定的要求，可以使用數組或者鏈表實現，算法簡單。 缺點：當數組個數n較大時，效率低下

數據挖掘十大算法總結--核心思想，算法優缺點，應用領域

data- 文本分類 target apr 排名 ans kmean 全部 等等 --------------------------

面試常考各類排序算法總結.(c#)

style index 存在 算法面試 變量 一位 選擇排序 直接插入 color 一. 面試以及考試過程中必會出現一道排序算法面試題，為了加深對排序算法的理解，在此我對各種排序算法做個總結歸納。 1.冒泡排序算法(BubbleSort) 1 public Class

算法總結——主席樹（poj2104）

() key orm 關於 data 分享 ogr d+ put 題目： Description You are working for Macrohard company in data structures department. After failing your

傳統神經網絡ANN訓練算法總結

deep ron sem 模型訓練 反向 mar reference 歸納 關系 傳統神經網絡ANN訓練算法總結 學習/訓練算法分類 神經網絡類型的不同，對應了不同類型的訓練/學習算法。因而根據神經網絡的分類，總結起來，傳統神經網絡的學習算法也可以

經常使用排序算法總結

i+1 下標 del sta end else return trac false #include<iostream> using namespace std; //show array void show(int *ar, int len) {

集成學習算法總結----Boosting和Bagging（轉）

原理 過程 訓練 嚴重 oos 機器學習 ppr 次數 error 1、集成學習概述 1.1 集成學習概述 集成學習在機器學習算法中具有較高的準去率，不足之處就是模型的訓練過程可能比較復雜，效率不是很高。目前接觸較多的集成學習主要有2種：基於Boosting的和基於Bagg

算法總結之 在兩個長度相等的排序數組中找到上中位數

pub system println bsp code null ima 方法 median 題目描述： arr1 和 arr2 長度都為N 求兩個數組中所有數的上中位數 要求 時間復雜度 O(logN) 額外空間復雜度O(1) 這道題目的方法比較好玩:

一致性hash與CRUSH算法總結

ldo 影響 tails 哈希函數 sch hash函數 結點 理解 數據 相同之處：都解決了數據緩存系統中數據如何存儲與路由。 不同之處：區別在於虛擬節點和物理節點的映射辦法不同 由於一般的哈希函數返回一個int（32bit）型的hashCode。因此，可以將該

算法總結之 打印兩個有序鏈表的公共部分

同時 cnblogs else ack style pan his pre pri 給定兩個有序鏈表的頭指針 head1 和 head2，打印兩個鏈表的公共部分 思路： 有序嘛， 如果head1 的值小於 head2, head1往下移動 如果head2的值小

算法總結之 數組中未出現的最小正整數

urn log 既然 color 一起 style 時間復雜度 復雜度 最終 給定一個無序整型數組arr，找到數組中未出現的最小正整數 解題思路非常好，需要好好學習一下，很邏輯 如果arr長度為N， 最優解可以做到時間復雜度O（N） 額外空間復雜度O(1) 1、

算法總結之 刪除鏈表的中間節點和a/b處的節點（鏈表中間節點的重要思想）

math 取整 算法 blog 總結 rem nod == while 給定鏈表的表頭節點head,實現刪除鏈表的中間節點的函數 推展： 給定鏈表的頭節點，整數a 和 整數 b,實現刪除a/b處節點的函數 先來分析原問題， 長度1 直接返回 長度2 將頭節點刪

算法總結之 反轉單向和雙向鏈表

while turn double logs pub pan != package port 分別實現反轉單向和雙向鏈表的函數 看代碼： package TT; public class Test88 { public class Node{

算法總結之 反轉部分單向鏈表

import class pos node span art cnblogs ++ != 給定單鏈表的表頭節點head, 以及兩個整數from 和 to, 在單向鏈表上把fro個節點到第to個節點這一部分進行反轉 思路： 本題 有可能存在換頭的問題，所以函數應該返回調整

算法總結之 復制含有隨機指針節點的鏈表

logs != imp 使用 turn ret 哈希表 算法 可能 一種特殊的鏈表節點類描述如下： public class Node{ public int value; public Node next; public Node rand;

算法總結之 兩個單鏈表相交的一些列問題

找到 開始 兩種 end 相交 說明 移動 一個 返回 單鏈表，可能有環，也可能無環。給定兩個單鏈表的頭節點head1 和 head2 這兩個鏈表可能交也可能不交。實現函數，如果相交，請返回相交的第一個節點，不交返回null 這道題目需要分析的情況非常 本題拆分