[學習opencv]Surface Matching之PPF Point Pair Feature 點對特徵
表面匹配簡介
具有3D結構感覺能力的相機和類似裝置正變得越來越普遍。 因此,使用深度和強度資訊來匹配3D物件(或部件)對於計算機視覺至關重要。 應用範圍從工業控制到指導視障人士的日常行為。 範圍影象中的識別和姿勢估計的任務旨在通過將所查詢的3D自由形式物件與所獲取的資料庫匹配來識別和定位所述3D自由形式物件。
從工業角度來看,使機器人能夠從垃圾箱中自動定位和拾取隨機放置和定向的物體是工廠自動化中的一項重要挑戰,取代了繁瑣而繁重的手工勞動。 系統應該能夠識別和定位具有預定義形狀的物體,並以夾持機器人拾取它所需的精度估計位置。 這是視覺引導機器人佔據舞臺的地方。 類似的工具還能夠通過非結構化環境引導機器人(甚至是人),從而實現自動導航。 這些屬性使得點雲的3D匹配無處不在。 在此背景下,我現在將描述使用3D特徵的3D物件識別和姿勢估計演算法的OpenCV實現。
基於三維特徵的曲面匹配演算法
為了實現任務3D匹配,演算法的狀態在很大程度上基於[41] ,這是該領域中提出的第一個和主要的實用方法之一。 該方法包括從深度影象或通用點雲中隨機提取3D特徵點,索引它們以及稍後在執行時有效地查詢它們。 僅考慮3D結構,並且使用普通雜湊表進行特徵查詢。
在充分意識到利用漂亮的CAD模型結構以實現智慧點取樣的同時,我現在將其放在一邊,以便尊重方法的普遍性(通常,對於這樣的演算法,不需要在CAD模型上進行培訓,點雲就足夠了)。 以下是整個演算法的概要:

演算法概要
如上所述,該演算法依賴於點對特徵的提取和索引,其定義如下:
\ [\ bf {{F}}(\ bf {{m1}},\ bf {{m2}})=(|| \ bf {{d}} || _2,<(\ bf {{n1}} ,\ bf {{d}}),<(\ bf {{n2}},\ bf {{d}}),<(\ bf {{n1}},\ bf {{n2}}))\]
其中\(\ bf {{m1}} \)和\(\ bf {{m2}} \)是模型(或場景)上兩個選定點的特徵,\(\ bf {{d}} \)是差異向量,\(\ bf {{n1}} \)和\(\ bf {{n2}} \)是\(\ bf {{m1}} \)和\(\ bf {m2} \的法線)。 在訓練階段,該向量被量化,索引。 在測試階段,從場景中提取相同的特徵並與資料庫進行比較。 通過諸如旋轉分量的分離之類的一些技巧,姿勢估計部分也可以變得有效(檢查參考以獲得更多細節)。 使用霍夫式投票和聚類來估計物件姿勢。 為了對姿勢進行聚類,原始姿勢假設按投票數的遞減順序排序。 從最高投票開始,建立一個新叢集。 如果下一個姿勢假設接近現有聚類之一,則將該假設新增到聚類中,並將聚類中心更新為聚類內姿勢假設的平均值。 如果下一個假設不接近任何群集,則會建立新群集。 接近測試是在平移和旋轉中使用固定閾值完成的。 用於平移的距離計算和平均在3D歐幾里德空間中執行,而用於旋轉的距離計算和平均是使用四元數表示來執行的。 在聚類之後,聚類按照總投票數的降序排序,這決定了估計姿勢的置信度。
使用\(ICP \)進一步細化該姿勢以獲得最終姿勢。
類似霍夫的投票計劃
如概要所示,在訓練階段期間,從模型中提取PPF(點對特徵),量化,儲存在散列表中並索引。 然而,在執行時期間,在輸入場景上執行類似的操作,除了這次執行對雜湊表的相似性查詢而不是插入。 此查詢還允許我們計算場景對的地平面變換。 在此之後,計算姿勢的旋轉分量減少到差值的計算\(\ alpha = \ alpha_m- \ alpha_s \)。 該元件帶有關於物件姿勢的提示。 在區域性模型座標向量和\(\ alpha \)上執行類似霍夫的投票方案。 為每個場景點實現的最高姿勢讓我們恢復物件姿勢。
PPF匹配的原始碼
// pc是模型的載入點雲
//(Nx6)和pcTest是一個載入點雲
//場景(Mx6)
ppf_match_3d :: PPF3D檢測器檢測器(0.03,0.05);
detector.trainModel(PC);
vector <Pose3DPtr>結果;
detector.match(pcTest,results,1.0 / 10.0,0.05);
cout << “Poses:” << endl;
//列印姿勢
for ( size_t i = 0; i <results.size(); i ++)
{
Pose3DPtr pose = results [i];
cout << “姿勢結果” << i << endl;
pose-> printPose();
}
通過ICP進行註冊
匹配過程終止於達到姿勢。 然而,由於多個匹配點,錯誤假設,姿勢平均等等,這種姿勢對噪聲非常開放,並且很多時候遠非完美。 儘管在該階段獲得的視覺結果令人滿意,但定量評估顯示出((10)度變化(誤差),這是可接受的匹配水平。 很多時候,要求可能遠遠超出此邊界,並且希望改進計算出的姿勢。
此外,在典型的RGBD場景和點雲中,由於場景中的可見性,3D結構僅能捕獲不到一半的模型。 因此,可以快速且正確地記錄遮擋和部分可見形狀的穩健姿態細化演算法不是不切實際的願望。
在這一點上,一個簡單的選擇是使用眾所周知的迭代最近點演算法。 然而,基本ICP的使用導致收斂慢,配準不良,異常值敏感以及未能記錄部分形狀。 因此,它絕對不適合這個問題。 出於這個原因,已經提出了許多變體。 不同的變體有助於姿勢估計過程的不同階段。
ICP由\(6 \)階段組成,我為每個階段提出的改進總結如下。
取樣
為了提高收斂速度和計算時間,通常使用比模型實際具有的更少的點。 然而,將正確的點取樣到暫存器本身就是一個問題。 天真的方式是統一取樣並希望獲得合理的子集。 更聰明的方法試圖找出關鍵點,這些關鍵點被認為對註冊過程有很大貢獻。 Gelfand等。 人。 利用協方差矩陣來約束本徵空間,從而使用影響平移和旋轉的一組點。 這是一種巧妙的子取樣方式,我將在實現中選擇使用它。
通訊搜尋
顧名思義,這一步實際上是以最接近的方式分配資料和模型中的點。 正確的分配將導致正確的姿勢,錯誤的分配會嚴重降低結果。 通常,KD樹用於搜尋最近鄰居,以提高速度。 然而,這不是最優保證,並且很多時候會導致錯誤的點匹配。 幸運的是,分配在迭代中得到糾正。
為了克服一些限制,Picky ICP [209]和BC-ICP(使用雙獨特對應的ICP )是兩種眾所周知的方法。 Picky ICP首先以老式方式找到對應關係,然後在得到的對應對中找到對應關係,如果將多個場景點\(p_i \)分配給同一個模型點\(m_j \),則選擇\(p_i \ )對應於最小距離。 另一方面,BC-ICP首先允許多個對應,然後通過建立雙唯一對應來解決分配。 它還定義了一種新穎的無對應異常值,它本質上簡化了識別異常值的過程。
作為參考,使用兩種方法。 由於P-ICP速度稍快,效能缺點不顯著,因此它將成為對應物再加工的首選方法。
對稱加權
在我的實現中,我目前不使用加權方案。 但常見的方法包括正常的相容性*(\(w_i = n ^ 1_i \ cdot n ^ 2_j \))或為較遠距離的點對分配較低的權重(\(w = 1- \ frac {|| dist(m_i, S_I)|| _2} {{dist_最大}} \))。
拒絕對
基於標準偏差的穩健估計,使用動態閾值來完成拒絕。 換句話說,在每次迭代中,我找到了Std的MAD估計值。 開發。 我將其表示為\(mad_i \)。 我拒絕距離為(d_i> \ tau mad_i \)的對。 這裡\(\ tau \)是拒絕的閾值,預設設定為\(3 \)。 在Picky細化之前應用加權,在前一階段進行了解釋。
錯誤度量標準
如上所述,使用[108]誤差度量中的點到平面的線性化。 這既加快了註冊過程又提高了收斂速度。
最小化
儘管提出了許多非線性優化器(例如Levenberg Mardquardt),但由於前一步驟中的線性化,姿態估計減少到求解線性方程組。 這就是我用DECOMP_SVD選項完全使用cv :: solve 。
ICP 演算法
已經描述了上述步驟,這裡我總結了ICP演算法的佈局。
通過點雲金字塔的高效ICP
雖然現在提出的變體很好地處理了一些異常值和錯誤的初始化,但它們需要大量的迭代。 然而,多解析度方案可以通過允許註冊從粗略級別開始並傳播到更低和更精細的級別來幫助減少迭代次數。 這種方法既改善了效能又提高了執行時間。
搜尋以分層方式通過多個級別完成。 註冊從一組非常粗略的模型樣本開始。 迭代地說,這些要點是經過密集和追求的。 在每次迭代之後,先前估計的姿勢被用作初始姿勢並且用ICP進行細化。
使用ICP進行姿態細化的原始碼
ICP icp(200,0.001f,2.5f,8);
//使用先前宣告的pc和pcTest
//這將為每個姿勢執行註冊
//包含在結果中
icp.registerModelToScene(pc,pcTest,results);
//結果現在包含精緻的姿勢
結果
本節專門介紹曲面匹配的結果(點對特徵匹配和以下ICP細化):

使用ppf + icp的單個青蛙模型的幾個匹配
Mian資料集的不同模型匹配如下:

Mian資料集的不同模型匹配
您可以在此處檢視 youTube上的視訊。
一個完整的樣本
引數調整
只要可能,表面匹配模組就會相對於模型直徑(軸平行邊界框的直徑)處理其引數。 這使得引數獨立於模型大小。 這就是為什麼模型和場景雲都被二次取樣,使得所有點的最小距離為\(RelativeSamplingStep * DimensionRange \),其中\(DimensionRange \)是沿給定維度的距離。 所有三個維度都以類似的方式進行取樣。 例如,如果\(RelativeSamplingStep \)設定為0.05且模型直徑為1m(1000mm),則從物件表面取樣的點將相距約50 mm。 從另一個角度來看,如果取樣RelativeSamplingStep設定為0.05,則最多生成\(20x20x20 = 8000 \)模型點(取決於模型填充卷的方式)。 因此,這導致最多8000x8000對。 實際上,由於模型不是均勻分佈在矩形稜鏡上,因此可以預期的點數要少得多。 減小此值可以產生更多的模型點,從而獲得更準確的表示。 但是,請注意,要計算的點對特徵的數量現在是二次增加的,因為複雜度為O(N ^ 2)。 對於32位系統而言,這尤其令人擔憂,因為大型模型很容易超出可用記憶體。 通常,對於大多數應用,0.025 - 0.05範圍內的值似乎是足夠的,其中預設值為0.03。 (注意,這個引數與[41]中給出的不同。在[41]中,使用一個統一的長方體進行量化,模型直徑用於取樣參考。在我的實現中,長方體是一個矩形稜柱,每個維度都是獨立量化的。我不參考直徑,而是沿著各個維度。
從模型中刪除異常值並最初準備理想模型是非常明智的。 這是因為,異常值直接影響相對計算並降低匹配精度。
在執行時階段,場景再次由\(RelativeSamplingStep \)取樣,如上所述。 但是這次,只有一部分場景點被用作參考。 此部分由引數\(RelativeSceneSampleStep \)控制,其中\(SceneSampleStep =(int)(1.0 / RelativeSceneSampleStep)\)。 換句話說,如果\(RelativeSceneSampleStep = 1.0 / 5.0 \),則子取樣場景將再次被均勻地取樣到點數的1/5。 此引數的最大值為1,增加此引數也會增加穩定性,但會降低速度。 同樣,由於初始場景無關的相對取樣,微調此引數並不是一個大問題。 當模型形狀均勻地佔據體積時,或者當模型形狀在量化體積內的微小位置被壓縮時(例如,八叉樹表示將具有太多的空單元),這將僅是問題。
\(RelativeDistanceStep \)充當散列表的離散化步驟。 點對特徵被量化以對映到散列表的桶。 這種離散化涉及乘法和整數的轉換。 理論上調整RelativeDistanceStep可控制碰撞率。 請注意,散列表上的更多衝突導致估計不太準確。 減小此引數會增加量化的影響,但會開始將不相似的點對分配給相同的分檔。 然而,增加它會減少對類似對進行分組的能力。 通常,因為在取樣階段,訓練模型點均勻地選擇,其距離由RelativeSamplingStep控制,RelativeDistanceStep預期等於該值。 同樣,0.025-0.05範圍內的值是明智的。 但是,此時,當模型密集時,建議不要降低此值。 對於嘈雜的場景,可以增加該值以提高匹配噪聲點的魯棒性。
________________________補充------------------------______________________________________________
PPF
機器人視覺中有一項重要人物就是從場景中提取物體的位置,姿態。影象處理演算法藉助Deep Learning 的東風已經在影象的物體標記領域耍的飛起了。而從三維場景中提取物體還有待研究。目前已有的思路是先提取關鍵點,再使用各種區域性特徵描述子對關鍵點進行描述,最後與待檢測物體進行比對,得到點-點的匹配。個別文章在之後還採取了ICP對匹配結果進行優化。
對於缺乏表面紋理資訊,或局部曲率變化很小,或點雲本身就非常稀疏的物體,採用區域性特徵描述子很難有效的提取到匹配對。所以就有了所謂基於Point Pair 的特徵,該特徵使用了一些全域性的資訊來進行匹配,更神奇的是,最終的位姿估計結果並不會陷入區域性最小值。詳細可參見論文:Model globally, match locally: Efficient and robust 3D object recognition. 與 Going further with point pair features。SLAM的重要研究方向object based Slam 也聲稱使用了Point Pair Feature進行匹配。
為了更好的理解這種方法,而在pcl中也沒有找到現成的演算法,所以我自己用matlab實現了一遍。
演算法的思想很簡單:
0、ppf 特徵為[d,<d,n1>,<d,n2>,<n1,n2>].
1、針對目標模型,在兩兩點之間構造點對特徵F,如果有N個點,那麼就有N*N個特徵(說明此演算法是O(N2)的),N*N個特徵形成特徵集F_Set
2、在場景中任意取1定點a,再任意取1動點b,構造ppf特徵,並從F_set中尋找對應的,那麼理想情況下,如果找到了完全匹配的特徵,則可獲得點雲匹配的結果。
3、此演算法是一種投票演算法,每次匹配都能得到一個旋轉角度,如果m個b都投票給了某一旋轉角度則可認為匹配成功
這個演算法最大的問題就是不停的取樣會導致極大的計算量。不過演算法本身確實可以匹配物體和場景。
ppf 特徵的構建
1 function obj = ppf(point1,point2) 2 d = point1.Location - point2.Location; 3 d_unit = d/norm(d); 4 apha1 = acos(point1.Normal*d_unit'); 5 apha2 = acos(point2.Normal*d_unit'); 6 apha3 = acos(point1.Normal*point2.Normal'); 7 obj = [norm(d),apha1,apha2,apha3]; 8 end
ppf 特徵集的構建


1 classdef modelFeatureSet < handle 2 %MODELFEATURESET 此處顯示有關此類的摘要 3 % 此處顯示詳細說明 4 5 properties 6 FeatureTree 7 ModelPointCloud 8 Pairs 9 end 10 11 methods 12 function obj = modelFeatureSet(pt) 13 obj.ModelPointCloud = copy(pt.removeInvalidPoints()); 14 end 15 function growTree(self) 16 self.ModelPointCloud = pcdownsample(self.ModelPointCloud,'GridAverage',.1); 17 pt_size = self.ModelPointCloud.Count; 18 idx = repmat(1:pt_size,pt_size,1); 19 tmp1 = reshape(idx,pt_size*pt_size,1); 20 tmp2 = reshape(idx',pt_size*pt_size,1); 21 pairs = [tmp1,tmp2]; 22 rnd = randseed(1,1000,1,1,pt_size*pt_size); 23 pairs = pairs(rnd,:); 24 Features = zeros(size(pairs,1),4); 25 for i = 1:size(pairs,1) 26 Features(i,:) = ppf(self.ModelPointCloud.select(pairs(i,1)),... 27 self.ModelPointCloud.select(pairs(i,2))); 28 end 29 self.FeatureTree = createns(Features); 30 self.Pairs = pairs; 31 end 32 end 33 end
PFH
正如點特徵表示法所示,表面法線和曲率估計是某個點周圍的幾何特徵基本表示法。雖然計算非常快速容易,但是無法獲得太多資訊,因為它們只使用很少的幾個引數值來近似表示一個點的k鄰域的幾何特徵。然而大部分場景中包含許多特徵點,這些特徵點有相同的或者非常相近的特徵值,因此採用點特徵表示法,其直接結果就減少了全域性的特徵資訊。本小節介紹三維特徵描述子中的一位成員:點特徵直方圖(Point Feature Histograms),我們簡稱為PFH,本小節將介紹它的理論優勢,從PCL實現的角度討論其實施細節。PFH特徵不僅與座標軸三維資料有關,同時還與表面法線有關。
理論基礎
PFH計算方式通過引數化查詢點與鄰域點之間的空間差異,並形成一個多維直方圖對點的k鄰域幾何屬性進行描述。直方圖所在的高維超空間為特徵表示提供了一個可度量的資訊空間,對點雲對應曲面的6維姿態來說它具有不變性,並且在不同的取樣密度或鄰域的噪音等級下具有魯棒性。點特徵直方圖(PFH)表示法是基於點與其k鄰域之間的關係以及它們的估計法線,簡言之,它考慮估計法線方向之間所有的相互作用,試圖捕獲最好的樣本表面變化情況,以描述樣本的幾何特徵。因此,合成特徵超空間取決於每個點的表面法線估計的質量。如圖1所示,表示的是一個查詢點(Pq)的PFH計算的影響區域,Pq 用紅色標註並放在圓球的中間位置,半徑為r,(Pq)的所有k鄰元素(即與點Pq的距離小於半徑r的所有點)全部互相連線在一個網路中。最終的PFH描述子通過計算鄰域內所有兩點之間關係而得到的直方圖,因此存在一個O(k)的計算複雜性。
圖1 查詢點 的PFH計算的影響區域
為了計算兩點Pi和Pj及與它們對應的法線Ni和Nj之間的相對偏差,在其中的一個點上定義一個固定的區域性座標系,如圖2所示。
圖2 定義一個固定的區域性座標系
使用上圖中uvw座標系,法線和之間的偏差可以用一組角度來表示,如下所示:
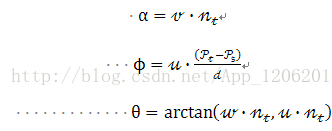
d是兩點Ps和Pt之間的歐氏距離,

為每一對點估計PFH四元組,可以使用:
computePairFeatures (const Eigen::Vector4f&p1,const Eigen::Vector4f&n1,
const Eigen::Vector4f&p2,const Eigen::Vector4f&n2,
float&f1,float&f2,float&f3,float&f4);
有關其他詳細資訊,請見API檔案。為查詢點建立最終的PFH表示,所有的四元組將會以某種統計的方式放進直方圖中,這個過程首先把每個特徵值範圍劃分為b個子區間,並統計落在每個子區間的點數目,因為四分之三的特徵在上述中為法線之間的角度計量,在三角化圓上可以將它們的引數值非常容易地歸一到相同的區間內。一個統計的例子是:把每個特徵區間劃分成等分的相同數目,為此在一個完全關聯的空間內建立有個區間的直方圖。在這個空間中,一個直方圖中某一區間統計個數的增一對應一個點的四個特徵值。如圖3所示,就是點雲中不同點的點特徵直方圖表示法的一個例子,在某些情況下,第四個特徵量d在通常由機器人捕獲的2.5維資料集中的並不重要,因為臨近點間的距離從視點開始是遞增的,而並非不變的,在掃描中區域性點密度影響特徵時,實踐證明省略d是有益的。
圖3 點雲中不同點的點特徵直方圖表示法
注意:更多相關資訊和數學推導,包括不同幾何體表面點雲的PFH特徵分析,請見[RusuDissertation]。
估計PFH特徵
點特徵直方圖(PFH)在PCL中的實現是pcl_features模組的一部分。預設PFH的實現使用5個區間分類(例如:四個特徵值中的每個都使用5個區間來統計),其中不包括距離(在上文中已經解釋過了——但是如果有需要的話,也可以通過使用者呼叫computePairFeatures方法來獲得距離值),這樣就組成了一個125浮點數元素的特徵向量(35),其儲存在一個pcl::PFHSignature125的點型別中。以下程式碼段將對輸入資料集中的所有點估計其對應的PFH特徵。
#include <pcl/point_types.h> //點型別標頭檔案
#include <pcl/features/pfh.h> //pfh特徵估計類標頭檔案
...//其他相關操作
pcl::PointCloud<pcl::PointXYZ>::Ptrcloud(newpcl::PointCloud<pcl::PointXYZ>);
pcl::PointCloud<pcl::Normal>::Ptrnormals(newpcl::PointCloud<pcl::Normal>());
...//開啟點雲檔案估計法線等
//建立PFH估計物件pfh,並將輸入點雲資料集cloud和法線normals傳遞給它
pcl::PFHEstimation<pcl::PointXYZ,pcl::Normal,pcl::PFHSignature125>pfh;
pfh.setInputCloud(cloud);
pfh.setInputNormals(normals);
//如果點雲是型別為PointNormal,則執行pfh.setInputNormals (cloud);
//建立一個空的kd樹表示法,並把它傳遞給PFH估計物件。
//基於已給的輸入資料集,建立kdtree
pcl::KdTreeFLANN<pcl::PointXYZ>::Ptrtree(newpcl::KdTreeFLANN<pcl::PointXYZ>());
pfh.setSearchMethod(tree);
//輸出資料集
pcl::PointCloud<pcl::PFHSignature125>::Ptrpfhs(newpcl::PointCloud<pcl::PFHSignature125>());
//使用半徑在5釐米範圍內的所有鄰元素。
//注意:此處使用的半徑必須要大於估計表面法線時使用的半徑!!!
pfh.setRadiusSearch(0.05);
//計算pfh特徵值
pfh.compute(*pfhs);
// pfhs->points.size ()應該與input cloud->points.size ()有相同的大小,即每個點都有一個pfh特徵向量
PFHEstimation類的實際計算程式內部只執行以下:
對點雲P中的每個點p
1.得到p點的最近鄰元素
2.對於鄰域內的每對點,計算其三個角度特徵引數值
3.將所有結果統計到一個輸出直方圖中
使用下列程式碼,從一個k-鄰域計算單一的PFH描述子:
computePointPFHSignature (const pcl::PointCloud<PointInT> &cloud,
const pcl::PointCloud<PointNT> &normals,
const std::vector<int> &indices,
int nr_split,
Eigen::VectorXf&pfh_histogram);
此處,cloud變數是包含點的輸入點雲,normals變數是包含對應cloud的法線的輸入點雲,indices代表輸入點雲(點與法線對應)中查詢點的k-近鄰元素集,nr_split是所分割槽間的數目,用於每個特徵區間的統計過程,pfh_histogram是浮點數向量來儲存輸出的合成直方圖。
FPFH
已知點雲P中有n個點,那麼它的點特徵直方圖(PFH)的理論計算複雜度是,其中k是點雲P中每個點p計算特徵向量時考慮的鄰域數量。對於實時應用或接近實時應用中,密集點雲的點特徵直方圖(PFH)的計算,是一個主要的效能瓶頸。本小節講述PFH計算方式的簡化形式,我們稱為快速點特徵直方圖FPFH(Fast Point Feature Histograms)(更多詳情,請見[RusuDissertation]),FPFH把演算法的計算複雜度降低到了,但是任然保留了PFH大部分的識別特性。
理論基礎
為了簡化直方圖的特徵計算,我們執行以下過程:
第一步,對於每一個查詢點,計算這個點和它的鄰域點之間的一個元組(參考上一節PFH的介紹),第一步結果我們稱之為簡化的點特徵直方圖SPFH(Simple Point Feature Histograms);
第二步,重新確定每個點的k鄰域,使用鄰近的SPFH值來計算的最終直方圖(稱為FPFH),如下所示:
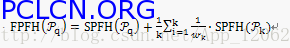
上式中,權重 在一些給定的度量空間中,表示查詢點 和其鄰近點 之間的距離,因此可用來評定一對點( , ),但是如果需要的話,也可以把用 另一種度量來表示。如圖1所示可以幫助理解這個權重方式的重要性,它表示的是以點為中心的k鄰域影響範圍。
圖1 以點 為中心的k鄰域影響範圍圖
因此,對於一個已知查詢點 ,這個演算法首先只利用 和它鄰域點之間對應對(上圖中以紅色線來說明),來估計它的SPFH值,很明顯這樣比PFH的標準計算少了鄰域點之間的互聯。點雲資料集中的所有點都要執行這一計算獲取SPFH,接下來使用它的鄰近點的SPFH值和點的SPFH值重新權重計算,從而得到點的最終FPFH值。FPFH計算新增的計算連線對,在上圖中以黑色線表示。如上圖所示,一些重要對點(與直接相連的點)被重複計數兩次(圖中以粗線來表示),而其他間接相連的用細黑線表示。
PFH和FPFH的區別
PFH和FPFH計算方式之間的主要區別總結如下:
1.FPFH沒有對全互連 點的所有鄰近點的計算引數進行統計,從圖12-18中可以看到,因此可能漏掉了一些重要的點對,而這些漏掉的對點可能對捕獲查詢點周圍的幾何特徵有貢獻。
2.PFH特徵模型是對查詢點周圍的一個精確的鄰域半徑內,而FPFH還包括半徑r範圍以外的額外點對(不過在2r內);
3.因為重新權重計算的方式,所以FPFH結合SPFH值,重新捕獲鄰近重要點對的幾何資訊;
4.由於大大地降低了FPFH的整體複雜性,因此FPFH有可能使用在實時應用中;
5.通過分解三元組,簡化了合成的直方圖。也就是簡單生成d分離特徵直方圖,對每個特徵維度來單獨繪製,並把它們連線在一起(見下2圖)。
圖2 PFH與FPFH示意圖
估計FPFH特徵
快速點特徵直方圖FPFH在點雲庫中的實現可作為pcl_features庫的一部分。預設的FPFH實現使用11個統計子區間(例如:四個特徵值中的每個都將它的引數區間分割為11個),特徵直方圖被分別計算然後合併得出了浮點值的一個33元素的特徵向量,這些儲存在一個pcl::FPFHSignature33點型別中。以下程式碼段將對輸入資料集中的所有點估計一組FPFH特徵值。
#include
#include //fpfh特徵估計類標頭檔案宣告
...//其他相關操作
pcl::PointCloud<pcl::PointXYZ>::Ptrcloud(newpcl::PointCloud<pcl::PointXYZ>);
pcl::PointCloud<pcl::Normal>::Ptrnormals(newpcl::PointCloud<pcl::Normal>());
...//開啟點雲檔案估計法線等
//建立FPFH估計物件fpfh,並把輸入資料集cloud和法線normals傳遞給它。
pcl::FPFHEstimation<pcl::PointXYZ,pcl::Normal,pcl::FPFHSignature33>fpfh;
fpfh.setInputCloud(cloud);
fpfh.setInputNormals(normals);
//如果點雲是型別為PointNormal,則執行fpfh.setInputNormals (cloud);
//建立一個空的kd樹物件tree,並把它傳遞給FPFH估計物件。
//基於已知的輸入資料集,建立kdtree
pcl::search::KdTree<PointXYZ>::Ptrtree(newpcl::search::KdTree<PointXYZ>);
fpfh.setSearchMethod(tree);
//輸出資料集
pcl::PointCloud<pcl::FPFHSignature33>::Ptrfpfhs(newpcl::PointCloud<pcl::FPFHSignature33>());
//使用所有半徑在5釐米範圍內的鄰元素
//注意:此處使用的半徑必須要大於估計表面法線時使用的半徑!!!
fpfh.setRadiusSearch(0.05);
//計算獲取特徵向量
fpfh.compute(*fpfhs);
//fpfhs->points.size ()應該和input cloud->points.size ()有相同的大小,即每個點有一個特徵向量
FPFHEstimation類的實際計算內部只執行以下操作:
對點雲P中的每個點p
第一步:
1.得到:math:`p`的鄰域元素
2. 計算每一對:math:`p, p_k`的三個角度引數值(其中:math:`p_k`是:math:`p`的鄰元素)
3.把所有結果統計輸出到一個SPFH直方圖
第二步:
1.得到:math:`p`的最近鄰元素
2.使用:math:`p`的每一個SPFH和一個權重計算式,來計算最終:math:`p`的FPFH
利用OpenMP提高FPFH速度
對於計算速度要求苛刻的使用者,PCL提供了一個FPFH估計的另一實現,它使用多核/多執行緒規範,利用OpenMP開發模式來提高計算速度。這個類的名稱是pcl::FPFHEstimationOMP,並且它的應用程式介面(API)100%相容單執行緒pcl::FPFHEstimation,這使它適合作為一個替換元件。在8核系統中,OpenMP的實現可以在6-8倍更快的計算時間內完全同樣單核系統上的計算。
RIFT描述子
論文:A sparse texture representation using local affine regions
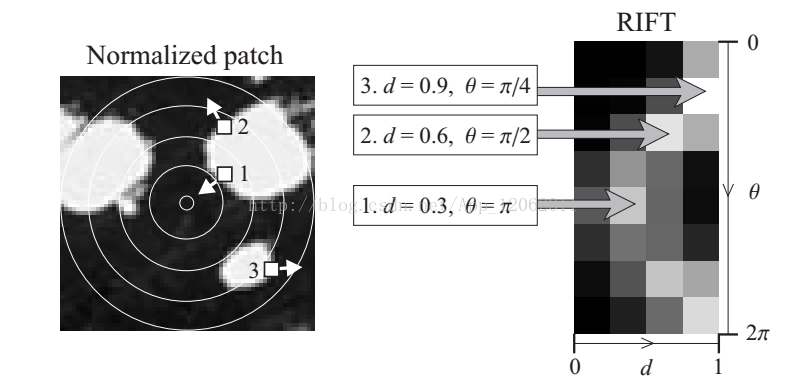
RIFT描述子,本質上來自於SIFT描述子,但是由於SIFT需要找到主方向,而RIFT考慮的是點雲資料中三維區域,因此。作者改進為如下結構:
也就是說,點P出一定範圍內,以點P為圓心,分割為等寬範圍內的同心圓。然後計算每個環內的梯度方向直方圖,為了保持旋轉不變性,以每個取樣點到圓心的距離和點梯度方向與圓心指向外部的梯度方向夾角作為統計特徵圖。作者使用了4個環和8個直方圖方向,形成一個32維描述子。