使用seaborn探索泰坦尼克號上乘客能否獲救
titanic資料集是個著名的資料集.kaggle上的titanic乘客生還率預測比賽是一個很好的入門機器學習的比賽.
資料集下載可以去https://www.kaggle.com/c/titanic/data.
本身寫這個系列筆記是作為自己機器學習的記錄,也為了加深自己對機器學習相關知識的理解.但是寫了前兩篇seaborn的筆記以後,感覺缺乏實際的比賽資料的例子,寫起來比較枯燥,讀的人看的可能也很枯燥,瀏覽量也寥寥.讀的人可能看完了會有一種,"哦,這樣啊,原來如此,懂了懂了",然鵝,一拿到真實的資料,還是一籌莫展,無從下手.
所以,今天就拿真實的資料來學習一下seaborn要怎麼用.怎麼在開始正式的機器學習演算法之前探索我們的資料關係.
titanic資料集給出了891行,12列已經標記的資料.即我們已知train.csv中891名乘客是否生還.我們需要預測test.csv中的418名乘客是否能夠生還.
首先看一眼我們的資料.
| Variable | Definition | Key |
|---|---|---|
| survival | Survival | 0 = No, 1 = Yes |
| pclass | Ticket class | 1 = 1st, 2 = 2nd, 3 = 3rd |
| sex | Sex | |
| Age | Age in years | |
| sibsp | # of siblings / spouses aboard the Titanic | |
| parch | # of parents / children aboard the Titanic | |
| ticket | Ticket number | |
| fare | Passenger fare | |
| cabin | Cabin number | |
| embarked | Port of Embarkation | C = Cherbourg, Q = Queenstown, S = Southampton |

意思是一名名字叫harris的22歲男性乘客,乘坐三等倉,船上有1個兄弟姐妹/配偶,0個父母/子女,在Southampton上船,票價7.25,在此次災難中沒有生還.
拿到資料,我有幾個簡單的設想
- 票的級別越高,越容易獲救 其實就是有錢有地位的容易獲救
- 票價越高越容易獲救 同上
- 兄弟姐妹或者父母子女多,容易獲救 因為可以互相幫助
- 女性更容易獲救
- 孩子更容易獲救
好了,下面用seaborn來畫畫圖,觀察一下我們的資料,看看我拿到資料後第一想法對不對.
我主要用catplot 和 displot來繪圖.
先來看看Pclass和Survived的關係.
catplot顧名思義,主要用來繪製分類資料(Categorical values).kind表示繪製什麼樣的圖,bar,box,violin等等.
sns.catplot(x="Pclass",y="Survived", kind="bar", data=titanic_train);
以此為例,我們的資料集中Pclass的取值共有3種,1,2,3,分別表示一等票,二等票,三等票.
當我們選擇bar圖時,y軸繪製出的是一個矩形,表示的是"Survived"這個資料的均值.(預設是均值,也可以調整為中位值).由於我們的Survived取值只有0(遇難了),1(獲救了).那麼均值等於獲救比例.
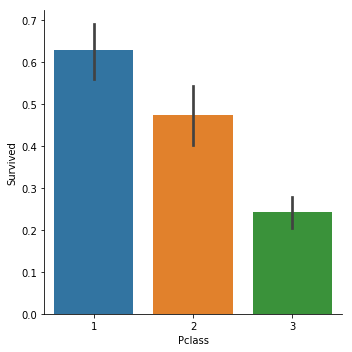
很明顯1等票的生還率更高.
再來看下票價和生還之間的關係.
票價的資料各種各樣,不像Pclass就3種.
sns.catplot(y="Fare",x="Survived", kind="bar", data=titanic_train);
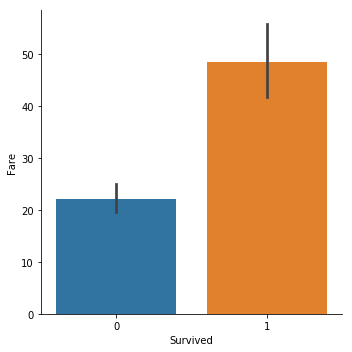
很明顯,獲救的人平均票價更高.
fare的值很多,我們想看看具體有哪些,大致的分佈,可以用box.
sns.catplot(y="Fare",x="Survived", kind="box", data=titanic_train);
box繪圖,會繪製出一個箱體,並標註出資料的25%(Q1),50%(Q2),75%(Q3)及outlier處的位置.
其中怎麼判斷哪些點是屬於異常值呢?根據IQR=Q3-Q1. 距離Q1或Q3的距離超過1.5IQR的就算是異常.
比如,下圖的Q1=12 Q2=26 Q3=57.那麼IQR=Q3-Q1=45. 超過Q3+1.5IQR=57+67.5=124.5的就會被算成異常點.會用黑色的小菱形繪製出來.
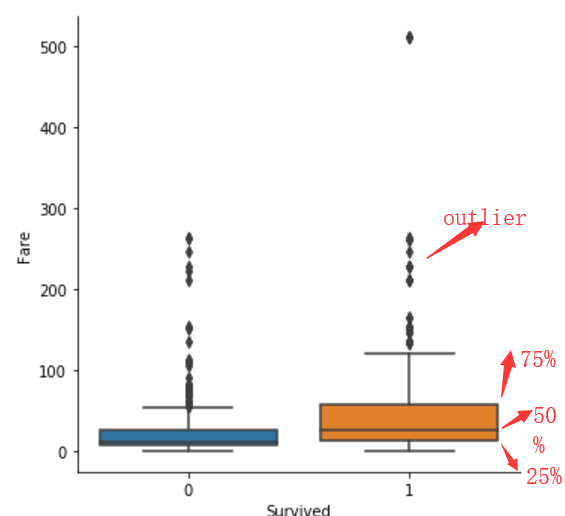
如果我們想要繪製出概率估計圖.則可以用displot,或者kdeplot.這個在之前的文章裡介紹過了.
sns.kdeplot(titanic_train["Fare"][(titanic_train["Survived"] == 1) & (titanic_train["Fare"].notnull())], shade=1, color='red')
sns.kdeplot(titanic_train["Fare"][(titanic_train["Survived"] == 0) & (titanic_train["Fare"].notnull())], shade=1, color='green');
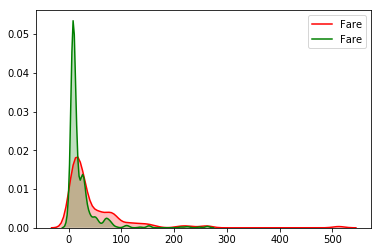
可以得到同樣的結論,票價高的,獲救概率更高一點.
注意:知識點來了
不止這一點,我們還看到,fare的分佈並不是正態分佈的,分佈的極其不規則,也就是所謂的資料偏移,可以看到高收入的分佈概率是很低的,但是高收入的樣本分佈確並不少,即假如我們把100認為高票價,一個人的票價是100以上的概率是很低的,但是在100-500之間分佈的確很多,各種各樣的都有.那機器學習演算法在處理這個資料的時候就要注意了,要對資料做處理,可以用log函式做轉換,或者你把0-20,20-50,50-100,100+的分別歸類為1(很低),2(一般),3(較貴),4(很貴),用這種思想也可以.
實際上,對這個資料的處理,讓我最終的預測率直接提高了2個百分點.
titanic_train["Fare"].skew()
可以通過這個skew()來檢測資料的偏移度.如果資料偏移度比較高的話,如果skew()>0.75,一般需要對資料做分佈變換,可以使用log變換.
這個skew()>0.75中的0.75怎麼來的,我不太清楚,可能是一種經驗值.我們的這個例子中skew()值已經接近5了.
下面來驗證我們的猜想3,家人越多越容易得救
sns.catplot(x="SibSp",y="Survived", kind="bar", data=titanic_train);
sns.catplot(x="Parch",y="Survived", kind="bar", data=titanic_train);

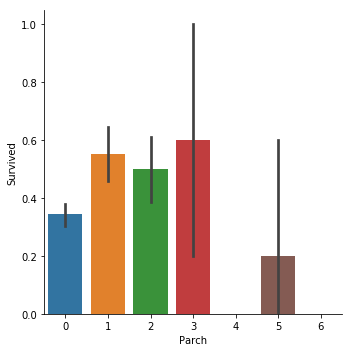
可以看到和我們的猜想並不一致,當有一個兄弟姐妹的時候,獲救概率大概有0.55.而有4個兄弟姐妹的時候,獲救概率反而只有0.15了.
在父母子女上,也是類似的,當父母子女達到5個的時候,獲救概率反而低了.
titanic_train["family"] = titanic_train["SibSp"] + titanic_train["Parch"] + 1
sns.catplot(x="family",y="Survived", kind="bar", data=titanic_train);
我們建立一個新特徵,家庭成員數,可以看到,當家庭人數比較少的時候,生還概率大.當家庭過於龐大,生還概率更低了.
猜想,是不是人少的時候,可以互相幫助,人多了,尋找家人會更困難,導致本可以獲救的最終因為尋找家人也沒活下來?

接下來看我們的猜想4,女人更容易獲救
sns.catplot(x="Sex",y="Survived", kind="bar", data=titanic_train);
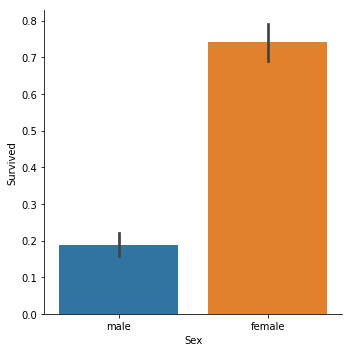
結論顯而易見,女性獲救概率高得多,lady first。
再來探索一下年齡與獲救的關係,驗證我們的猜想5.
sns.catplot(y="Age",x="Survived", kind="bar", data=titanic_train);

生還乘客的平均年齡是低了一點,但是兩者區別不大,也都在正常區間,似乎看不出來什麼.
我們來看看概率估計.
sns.kdeplot(titanic_train["Age"][(titanic_train["Survived"] == 1) & (titanic_train["Age"].notnull())], shade=1, color='red')
sns.kdeplot(titanic_train["Age"][(titanic_train["Survived"] == 0) & (titanic_train["Age"].notnull())], shade=1, color='green');
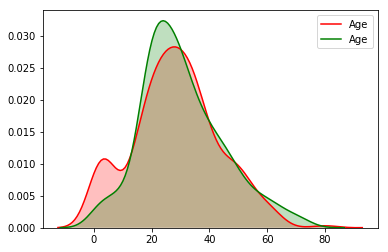
這個圖就很明顯了,在age很小的時候,紅線(獲救)明顯有個波峰.說明在這個年級段,獲救概率更高. 在age很大的時候(60歲以上),
綠線在紅線之上,說明老人更可能遇難.
至此我們的5個猜想基本被驗證,除了猜想3. 說明直覺還是比較準的嘛.
現在還剩下Name,Ticket,Cabin,Embarked這4個特徵與Survived的關係沒有驗證.
其中Name,Ticket,Cabin都是不規則的字串,需要做更多的特徵工程,找到其中的規律以後,才好觀察資料之間的關係.Embarked的取值只有S,C,Q3種.我們來看下Embarked與Survived的關係.
老套路:
sns.catplot(y="Survived", x = "Embarked",data = titanic_train, kind="bar")
C = Cherbourg, Q = Queenstown, S = Southampton
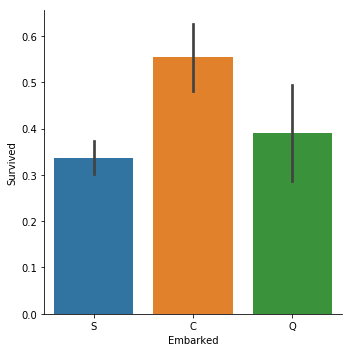
說實話,這個真的非常出乎我的意料.我原以為,是否生還和上船港口沒有關係,三者的生還概率應該是基本一樣才對.
然後我就開始胡思亂想了,總不能Cherbourg登船的人命好吧,越想越沒道理.或者說Cherbourg登船的人都坐在船的某個位置,受到冰山撞擊比較小?又或者只是因為樣本數量太少了,是個偶然的巧合?
然後我想到是不是這個港口登船的都是有錢人?
sns.catplot(y="Fare", x = "Embarked",data = titanic_train, kind="bar")
sns.catplot(x="Pclass", hue="Embarked", data=titanic_train,kind="count")
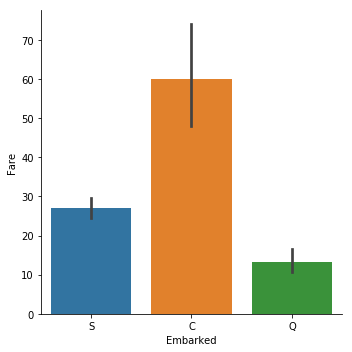
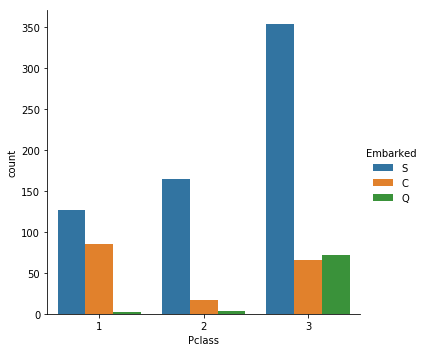
這麼一看,還真是.所以Embarked=C的乘客生還概率高不是什麼偶然.
所以這就引發了一個問題,資料之間其實有關聯的,比如Embarked和Fare就有一定的相關性.我們可以用heatmap來探索各個特徵資料之間的相關性.
sns.heatmap(titanic_train.corr(),annot=True,fmt ='.2f')
titanic_train.corr()計算出來的是各個特徵的皮爾遜相關係數.皮爾遜相關係數。 wiki上解釋一大堆,說實在的裡面很多數學和統計學上的公式我沒看懂.其實我們也不需要搞的特別清楚這些數學公式. 說白了,皮爾遜相關係數就是求兩個向量之間的距離或者說夾角,越小越相關.(這個說法不嚴謹,但是原理上這麼理解是沒問題的).皮爾遜相關係數求出來在-1到1之間.

因為是求向量之間距離,所以展示的只有特徵值是數字型的特徵,Embarked特徵的值是字元,所以沒展示.你可以把字元對映成數字,比如S-->1,C-->2,Q-->3,再計算皮爾遜相關係數.當然這樣做是有問題的.因為,S,C,Q本來不存在大小關係,這麼對映以後存在了大小關係.這裡涉及到一個one-hot編碼問題.有興趣的自己搜尋一下,這篇就先不講了.
ok,以上就是本篇文章使用seaborn探索titanic資料的內容,更多有趣有用的關於資料預處理視覺化,關於seaborn使用等著大家去學習探索.希望這篇文章對大家有幫助和啟發.
