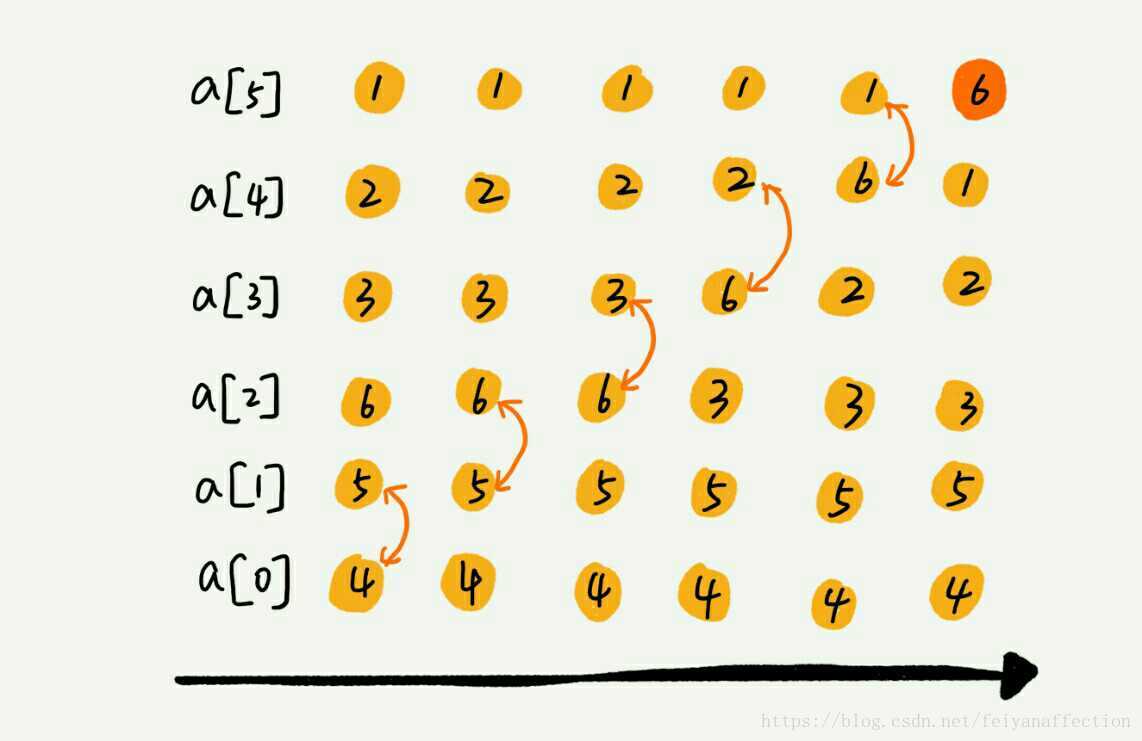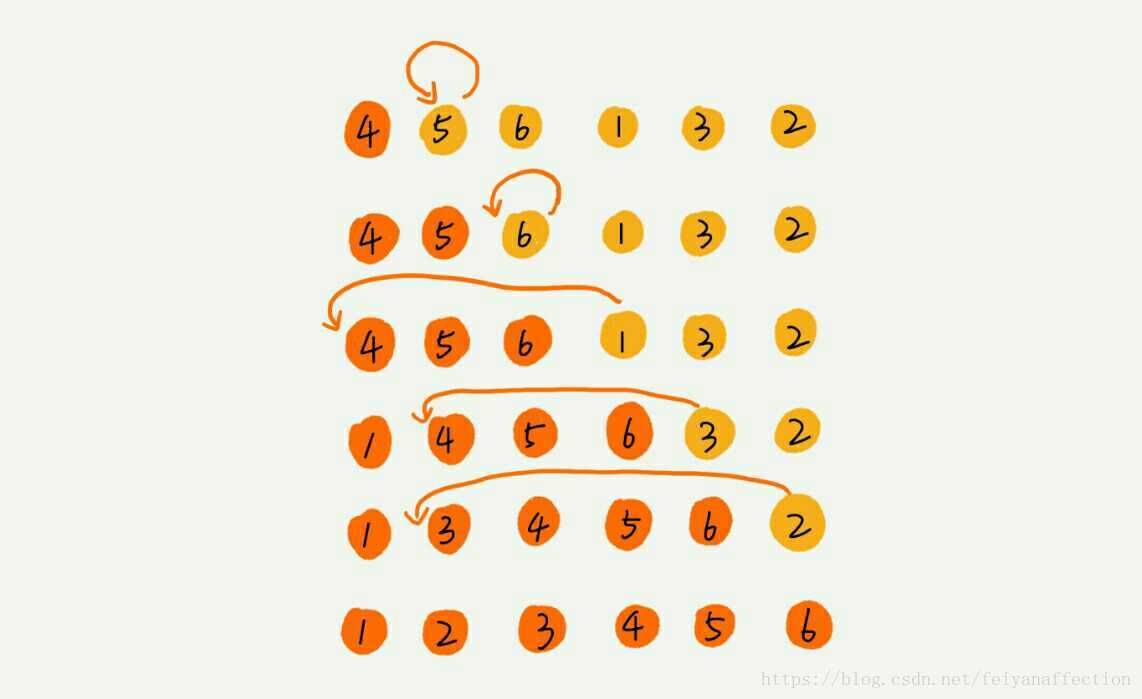10-排序(上):為什麼插入排序比氣泡排序更受歡迎?
排序對於任何一個程式設計師來說,可能都不會陌生。你學的第一個演算法,可能就是排序。大部分程式語言中,也都提供了排序函式。在平常的專案中,我們也經常會用到排序。排序非常重要,所以我會花多一點時間來詳細講一講經典的排序演算法。
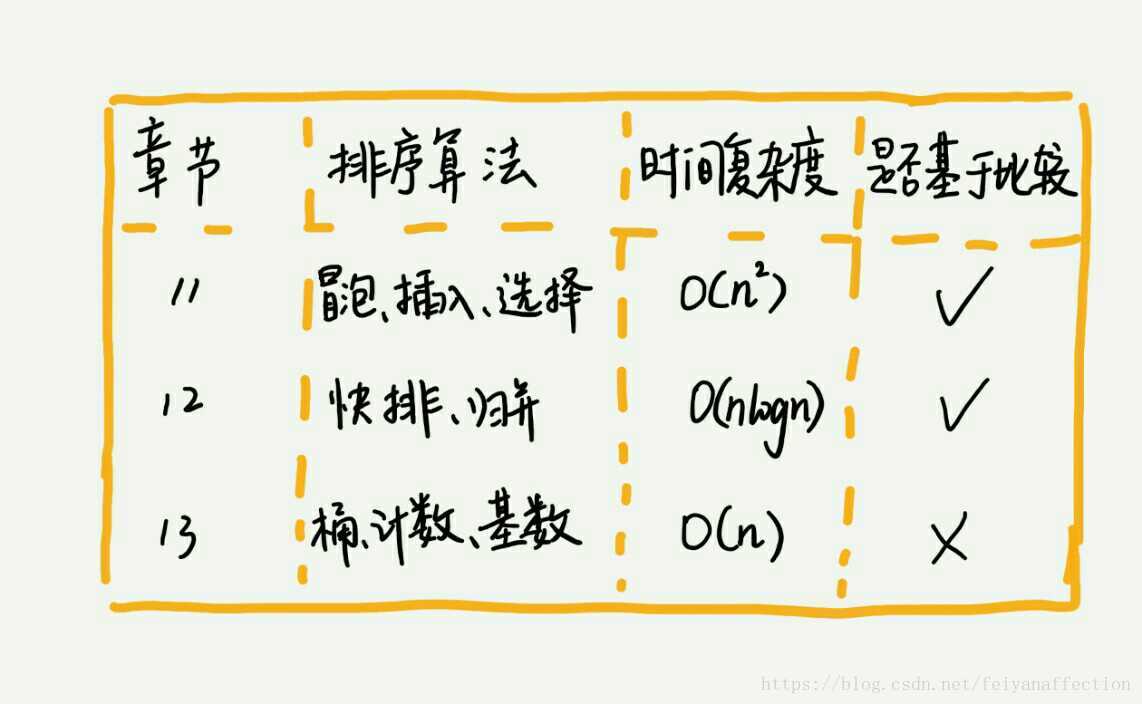
排序演算法太多了,有很多可能你連名字都沒聽說過,比如猴子排序、睡眠排序、麵條排序等。我只講眾多排序演算法中的一小撮,也是最經典的、最常用的:氣泡排序、插入排序、選擇排序、歸併排序、快速排序、計數排序、基數排序、桶排序。我按照時間複雜度把它們分成了三類,分三節課來講解。
帶著問題去學習,是最有效的學習方法。所以按照慣例,我還是先給你出一個思考題:插入排序和氣泡排序的時間複雜度相同,都是 O(n2),在實際的軟體開發裡,為什麼我們更傾向於使用插入排序演算法而不是氣泡排序演算法呢?
你可以先思考一兩分鐘,帶著這個問題,我們開始今天的內容!
如何分析一個“排序演算法”? 學習排序演算法,我們除了學習它的演算法原理、程式碼實現之外,更重要的是要學會如何評價、分析一個排序演算法。那分析一個排序演算法,要從哪幾個方面入手呢?
排序演算法的執行效率 對於排序演算法執行效率的分析,我們一般會從這幾個方面來衡量:
1. 最好情況、最壞情況、平均情況時間複雜度
我們在分析排序演算法的時間複雜度時,要分別給出最好情況、最壞情況、平均情況下的時間複雜度。除此之外,你還要說出最好、最壞時間複雜度對應的要排序的原始資料是什麼樣的。
為什麼要區分這三種時間複雜度呢?第一,有些排序演算法會區分,為了好對比,所以我們最好都做一下區分。第二,對於要排序的資料,有的接近有序,有的完全無序。有序度不同的資料,對於排序的執行時間肯定是有影響的,我們要知道排序演算法在不同資料下的效能表現。
2. 時間複雜度的係數、常數 、低階
我們知道,時間複雜度反應的是資料規模 n 很大的時候的一個增長趨勢,所以它表示的時候會忽略係數、常數、低階。但是實際的軟體開發中,我們排序的可能是 10 個、100 個、1000 個這樣規模很小的資料,所以,在對同一階時間複雜度的排序演算法效能對比的時候,我們就要把係數、常數、低階也考慮進來。
3. 比較次數和交換(或移動)次數
這一節和下一節講的都是基於比較的排序演算法。基於比較的排序演算法的執行過程,會涉及兩種操作,一種是元素比較大小,另一種是元素交換或移動。所以,如果我們在分析排序演算法的執行效率的時候,應該把比較次數和交換(或移動)次數也考慮進去。
排序演算法的記憶體消耗
排序演算法的穩定性 僅僅用執行效率和記憶體消耗來衡量排序演算法的好壞是不夠的。針對排序演算法,我們還有一個重要的度量指標,穩定性。這個概念是說,如果待排序的序列中存在值相等的元素,經過排序之後,相等元素之間原有的先後順序不變。
我通過一個例子來解釋一下。比如我們有一組資料 2,9,3,4,8,3,按照大小排序之後就是 2,3,3,4,8,9。
這組資料裡有兩個 3。經過某種排序演算法排序之後,如果兩個 3 的前後順序沒有改變,那我們就把這種排序演算法叫作穩定的排序演算法;如果前後順序發生變化,那對應的排序演算法就叫作不穩定的排序演算法。
你可能要問了,兩個 3 哪個在前,哪個在後有什麼關係啊,穩不穩定又有什麼關係呢?為什麼要考察排序演算法的穩定性呢?
很多資料結構和演算法課程,在講排序的時候,都是用整數來舉例,但在真正軟體開發中,我們要排序的往往不是單純的整數,而是一組物件,我們需要按照物件的某個 key 來排序。
比如說,我們現在要給電商交易系統中的“訂單”排序。訂單有兩個屬性,一個是下單時間,另一個是訂單金額。如果我們現在有 10 萬條訂單資料,我們希望按照金額從小到大對訂單資料排序。對於金額相同的訂單,我們希望按照下單時間從早到晚有序。對於這樣一個排序需求,我們怎麼來做呢?
最先想到的方法是:我們先按照金額對訂單資料進行排序,然後,再遍歷排序之後的訂單資料,對於每個金額相同的小區間再按照下單時間排序。這種排序思路理解起來不難,但是實現起來會很複雜。
藉助穩定排序演算法,這個問題可以非常簡潔地解決。解決思路是這樣的:我們先按照下單時間給訂單排序,注意是按照下單時間,不是金額。排序完成之後,我們用穩定排序演算法,按照訂單金額重新排序。兩遍排序之後,我們得到的訂單資料就是按照金額從小到大排序,金額相同的訂單按照下單時間從早到晚排序的。為什麼呢?
穩定排序演算法可以保持金額相同的兩個物件,在排序之後的前後順序不變。第一次排序之後,所有的訂單按照下單時間從早到晚有序了。在第二次排序中,我們用的是穩定的排序演算法,所以經過第二次排序之後,相同金額的訂單仍然保持下單時間從早到晚有序。
氣泡排序(Bubble Sort) 我們從氣泡排序開始,學習今天的三種排序演算法。
氣泡排序只會操作相鄰的兩個資料。每次冒泡操作都會對相鄰的兩個元素進行比較,看是否滿足大小關係要求。如果不滿足就讓它倆互換。一次冒泡會讓至少一個元素移動到它應該在的位置,重複 n 次,就完成了 n 個數據的排序工作。
我用一個例子,帶你看下氣泡排序的整個過程。我們要對一組資料 4,5,6,3,2,1,從小到到大進行排序。第一次冒泡操作的詳細過程就是這樣:
可以看出,經過一次冒泡操作之後,6 這個元素已經儲存在正確的位置上。要想完成所有資料的排序,我們只要進行 6 次這樣的冒泡操作就行了。
實際上,剛講的冒泡過程還可以優化。當某次冒泡操作已經沒有資料交換時,說明已經達到完全有序,不用再繼續執行後續的冒泡操作。我這裡還有另外一個例子,這裡面給 6 個元素排序,只需要 4 次冒泡操作就可以了。
氣泡排序演算法的原理比較容易理解,具體的程式碼我貼到下面,你可以結合著程式碼來看我前面講的原理。
// 氣泡排序,a 表示陣列,n 表示陣列大小
public void bubbleSort(int[] a, int n) {
if (n <= 1) return;
for (int i = 0; i < n; ++i) {
// 提前退出冒泡迴圈的標誌位
boolean flag = false;
for (int j = 0; j < n - i - 1; ++j) {
if (a[j] > a[j+1]) { // 交換
int tmp = a[j];
a[j] = a[j+1];
a[j+1] = tmp;
flag = true; // 表示有資料交換
}
}
if (!flag) break; // 沒有資料交換,提前退出
}
}
現在,結合剛才我分析排序演算法的三個方面,我有三個問題要問你。
第一,氣泡排序是原地排序演算法嗎?
冒泡的過程只涉及相鄰資料的交換操作,只需要常量級的臨時空間,所以它的空間複雜度為 O(1),是一個原地排序演算法。
第二,氣泡排序是穩定的排序演算法嗎?
在氣泡排序中,只有交換才可以改變兩個元素的前後順序。為了保證氣泡排序演算法的穩定性,當有相鄰的兩個元素大小相等的時候,我們不做交換,相同大小的資料在排序前後不會改變順序,所以氣泡排序是穩定的排序演算法。
第三,氣泡排序的時間複雜度是多少?
最好情況下,要排序的資料已經是有序的了,我們只需要進行一次冒泡操作,就可以結束了,所以最好情況時間複雜度是 O(n)。而最壞的情況是,要排序的資料剛好是倒序排列的,我們需要進行 n 次冒泡操作,所以最壞情況時間複雜度為 O(n2)。
最好、最壞情況下的時間複雜度很容易分析,那平均情況下的時間複雜是多少呢?我們前面講過,平均時間複雜度就是加權平均期望時間複雜度,分析的時候要結合概率論的知識。
對於包含 n 個數據的陣列,這 n 個數據就有 n! 種排列方式。不同的排列方式,氣泡排序執行的時間肯定是不同的。比如我們前面舉的那兩個例子,其中一個要進行 6 次冒泡,而另一個只需要 4 次。如果用概率論方法定量分析平均時間複雜度,涉及的數學推理和計算就會很複雜。我這裡還有一種思路,通過“有序度”和“逆序度”這兩個概念來進行分析。
有序度是陣列中具有有序關係的元素對的個數。有序元素對用數學表示式表示就是這樣:
有序元素對:a[i] <= a[j], 如果 i < j。
同理,對於一個倒序排列的陣列,比如 6,5,4,3,2,1,有序度是 0;對於一個完全有序的陣列,比如 1,2,3,4,5,6,有序度就是n*(n-1)/2,也就是 15。我們把這種完全有序的陣列的有序度叫作滿有序度。
逆序度的定義正好跟有序度相反(預設從小到大為有序),我想你應該已經想到了。關於逆序度,我就不舉例子講了。你可以對照我講的有序度的例子自己看下。
逆序元素對:a[i] > a[j], 如果 i < j。 關於這三個概念,我們還可以得到一個公式:逆序度 = 滿有序度 - 有序度。我們排序的過程就是一種增加有序度,減少逆序度的過程,最後達到滿有序度,就說明排序完成了。
我還是拿前面舉的那個氣泡排序的例子來說明。要排序的陣列的初始狀態是 4,5,6,3,2,1 ,其中,有序元素對有 (4,5) (4,6)(5,6),所以有序度是 3。n=6,所以排序完成之後終態的滿有序度為 n*(n-1)/2=15。
氣泡排序包含兩個操作原子,比較和交換。每交換一次,有序度就加 1。不管演算法怎麼改進,交換次數總是確定的,即為逆序度,也就是n*(n-1)/2–初始有序度。此例中就是 15–3=12,要進行 12 次交換操作。
對於包含 n 個數據的陣列進行氣泡排序,平均交換次數是多少呢?最壞情況下,初始狀態的有序度是 0,所以要進行 n*(n-1)/2 次交換。最好情況下,初始狀態的有序度是 n*(n-1)/2,就不需要進行交換。我們可以取箇中間值 n*(n-1)/4,來表示初始有序度既不是很高也不是很低的平均情況。
換句話說,平均情況下,需要 n*(n-1)/4 次交換操作,比較操作肯定要比交換操作多,而複雜度的上限是 O(n2),所以平均情況下的時間複雜度就是 O(n2)。
這個平均時間複雜度推導過程其實並不嚴格,但是很多時候很實用,畢竟概率論的定量分析太複雜,不太好用。等我們講到快排的時候,我還會再次用這種“不嚴格”的方法來分析平均時間複雜度。
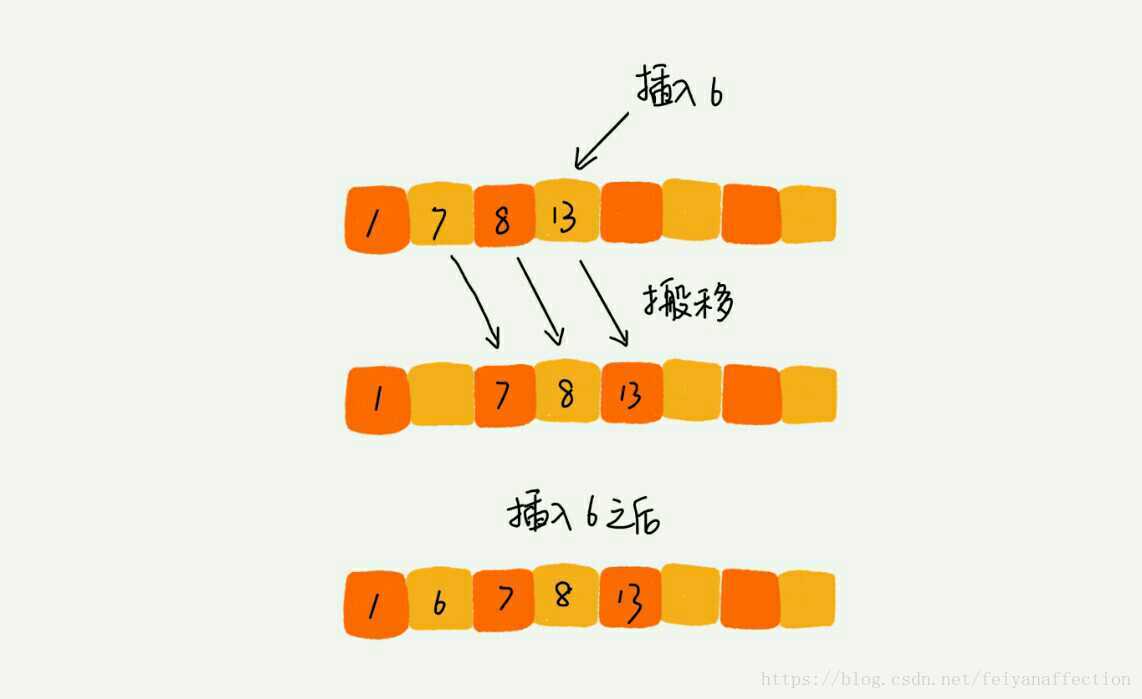
插入排序(Insertion Sort) 我們先來看一個問題。一個有序的陣列,我們往裡面新增一個新的資料後,如何繼續保持資料有序呢?很簡單,我們只要遍歷陣列,找到資料應該插入的位置將其插入即可。
這是一個動態排序的過程,即動態地往有序集合中新增資料,我們可以通過這種方法保持集合中的資料一直有序。而對於一組靜態資料,我們也可以借鑑上面講的插入方法,來進行排序,於是就有了插入排序演算法。
那插入排序具體是如何藉助上面的思想來實現排序的呢?
首先,我們將陣列中的資料分為兩個區間,已排序區間和未排序區間。初始已排序區間只有一個元素,就是陣列的第一個元素。插入演算法的核心思想是取未排序區間中的元素,在已排序區間中找到合適的插入位置將其插入,並保證已排序區間資料一直有序。重複這個過程,直到未排序區間中元素為空,演算法結束。
如圖所示,要排序的資料是 4,5,6,1,3,2,其中左側為已排序區間,右側是未排序區間。
插入排序也包含兩種操作,一種是元素的比較,一種是元素的移動。當我們需要將一個數據 a 插入到已排序區間時,需要拿 a 與已排序區間的元素依次比較大小,找到合適的插入位置。找到插入點之後,我們還需要將插入點之後的元素順序往後移動一位,這樣才能騰出位置給元素 a 插入。
對於不同的查詢插入點方法(從頭到尾、從尾到頭),元素的比較次數是有區別的。但對於一個給定的初始序列,移動操作的次數總是固定的,就等於逆序度。
為什麼說移動次數就等於逆序度呢?我拿剛才的例子畫了一個圖表,你一看就明白了。滿有序度是 n*(n-1)/2=15,初始序列的有序度是 5,所以逆序度是 10。插入排序中,資料移動的個數總和也等於 10=3+3+4。
插入排序的原理也很簡單吧?我也將程式碼實現貼在這裡,你可以結合著程式碼再看下。
// 插入排序,a 表示陣列,n 表示陣列大小
public void insertionSort(int[] a, int n) {
if (n <= 1) return;
for (int i = 1; i < n; ++i) {
int value = a[i];
int j = i - 1;
// 查詢插入的位置
for (; j >= 0; --j) {
if (a[j] > value) {
a[j+1] = a[j]; // 資料移動
} else {
break;
}
}
a[j+1] = value; // 插入資料
}
}
現在,我們來看點稍微複雜的東西。我這裡還是有三個問題要問你。
第一,插入排序是原地排序演算法嗎?
從實現過程可以很明顯地看出,插入排序演算法的執行並不需要額外的儲存空間,所以空間複雜度是 O(1),也就是說,這是一個原地排序演算法。
第二,插入排序是穩定的排序演算法嗎?
在插入排序中,對於值相同的元素,我們可以選擇將後面出現的元素,插入到前面出現元素的後面,這樣就可以保持原有的前後順序不變,所以插入排序是穩定的排序演算法。
第三,插入排序的時間複雜度是多少?
如果要排序的資料已經是有序的,我們並不需要搬移任何資料。如果我們從尾到頭在有序資料組裡面查詢插入位置,每次只需要比較一個數據就能確定插入的位置。所以這種情況下,最好是時間複雜度為 O(n)。注意,這裡是從尾到頭遍歷已經有序的資料。
如果陣列是倒序的,每次插入都相當於在陣列的第一個位置插入新的資料,所以需要移動大量的資料,所以最壞情況時間複雜度為 O(n2)。
還記得我們在陣列中插入一個數據的平均時間複雜度是多少嗎?沒錯,是 O(n)。所以,對於插入排序來說,每次插入操作都相當於在陣列中插入一個數據,迴圈執行 n 次插入操作,所以平均時間複雜度為 O(n2)。
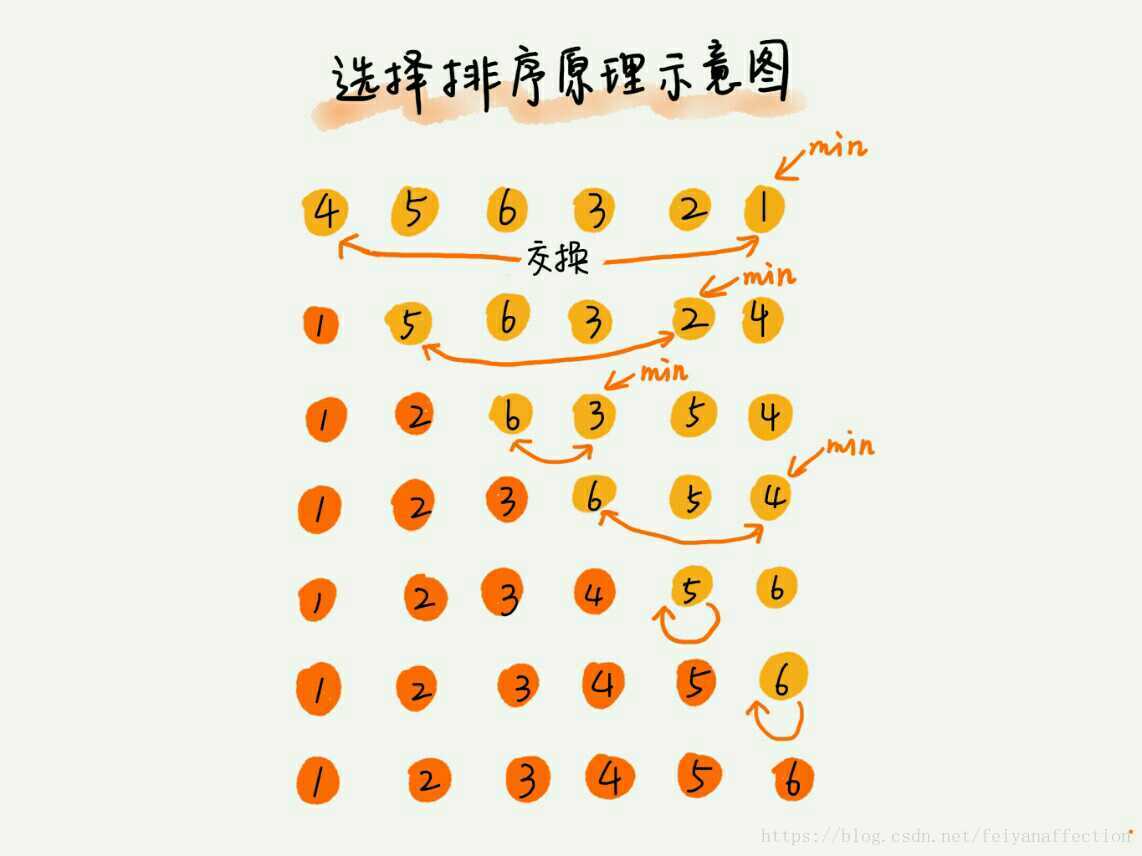
選擇排序(Selection Sort) 選擇排序演算法的實現思路有點類似插入排序,也分已排序區間和未排序區間。但是選擇排序每次會從未排序區間中找到最小的元素,將其放到已排序區間的末尾。
照例,也有三個問題需要你思考,不過前面兩種排序演算法我已經分析得很詳細了,這裡就直接公佈答案了。
首先,選擇排序空間複雜度為 O(1),是一種原地排序演算法。選擇排序的最好情況時間複雜度、最壞情況和平均情況時間複雜度都為 O(n2)。你可以自己來分析看看。
那選擇排序是穩定的排序演算法嗎?
答案是否定的,選擇排序是一種不穩定的排序演算法。從我前面畫的那張圖中,你可以看出來,選擇排序每次都要找剩餘未排序元素中的最小值,並和前面的元素交換位置,這樣破壞了穩定性。
比如 5,8,5,2,9 這樣一組資料,使用選擇排序演算法來排序的話,第一次找到最小元素 2,與第一個 5 交換位置,那第一個 5 和中間的 5 順序就變了,所以就不穩定了。正是因此,相對於氣泡排序和插入排序,選擇排序就稍微遜色了。
解答開篇 基本的知識都講完了,我們來看開篇的問題:氣泡排序和插入排序的時間複雜度都是 O(n2),都是原地排序演算法,為什麼插入排序要比氣泡排序更受歡迎呢?
我們前面分析氣泡排序和插入排序的時候講到,氣泡排序不管怎麼優化,元素交換的次數是一個固定值,是原始資料的逆序度。插入排序是同樣的,不管怎麼優化,元素移動的次數也等於原始資料的逆序度。
但是,從程式碼實現上來看,氣泡排序的資料交換要比插入排序的資料移動要複雜,氣泡排序需要 3 個賦值操作,而插入排序只需要 1 個。我們來看這段操作:
氣泡排序中資料的交換操作:
if (a[j] > a[j+1]) { // 交換
int tmp = a[j];
a[j] = a[j+1];
a[j+1] = tmp;
flag = true;
}
插入排序中資料的移動操作:
if (a[j] > value) {
a[j+1] = a[j]; // 資料移動
} else {
break;
}
我們把執行一個賦值語句的時間粗略地計為單位時間(unit_time),然後分別用氣泡排序和插入排序對同一個逆序度是 K 的陣列進行排序。用氣泡排序,需要 K 次交換操作,每次需要 3 個賦值語句,所以交換操作總耗時就是 3*K 單位時間。而插入排序中資料移動操作只需要 K 個單位時間。
這個只是我們非常理論的分析,為了實驗,針對上面的氣泡排序和插入排序的 Java 程式碼,我寫了一個性能對比測試程式,隨機生成 10000 個數組,每個陣列中包含 200 個數據,然後在我的機器上分別用冒泡和插入排序演算法來排序,氣泡排序演算法大約 700ms 才能執行完成,而插入排序只需要 100ms 左右就能搞定!
所以,雖然氣泡排序和插入排序在時間複雜度上是一樣的,都是 O(n2),但是如果我們希望把效能優化做到極致,那肯定首選插入排序。插入排序的演算法思路也有很大的優化空間,我們只是講了最基礎的一種。如果你對插入排序的優化感興趣,可以自行學習一下希爾排序。
內容小結?
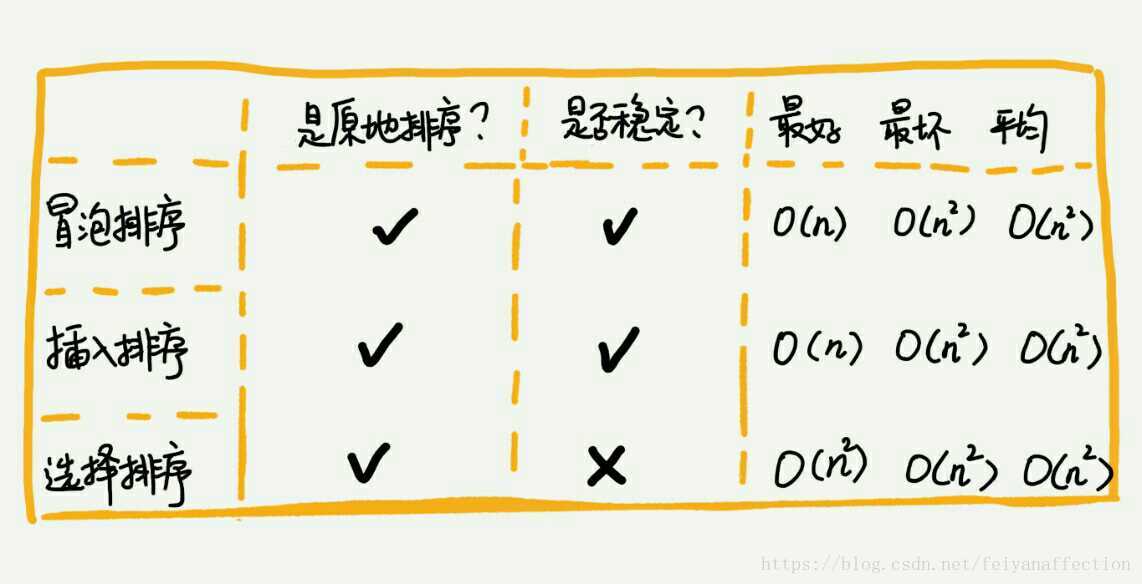
要想分析、評價一個排序演算法,需要從執行效率、記憶體消耗和穩定性三個方面來看。因此,這一節,我帶你分析了三種時間複雜度是 O(n2) 的排序演算法,氣泡排序、插入排序、選擇排序。你需要重點掌握的是它們的分析方法。
這三種時間複雜度為 O(n2) 的排序演算法中,氣泡排序、選擇排序,可能就純粹停留在理論的層面了,學習的目的也只是為了開拓思維,實際開發中應用並不多,但是插入排序還是挺有用的。後面講排序優化的時候,我會講到,有些程式語言中的排序函式的實現原理會用到插入排序演算法。
今天講的這三種排序演算法,實現程式碼都非常簡單,對於小規模資料的排序,用起來非常高效。但是在大規模資料排序的時候,這個時間複雜度還是稍微有點高,所以我們更傾向於用下一節要講的時間複雜度為 O(nlogn) 的排序演算法。
課後思考 我們講過,特定演算法是依賴特定的資料結構的。我們今天講的幾種排序演算法,都是基於陣列實現的。如果資料儲存在連結串列中,這三種排序演算法還能工作嗎?如果能,那相應的時間、空間複雜度又是多少呢?
一、對於課後題,覺得應該有個前提,是否允許修改連結串列的節點value值,還是隻能改變節點的位置?
一般而言,考慮只能改變節點位置,氣泡排序相比於陣列實現,比較次數一致,但交換時操作更復雜;插入排序,比較次數一致,不需要再有後移操作,找到位置後可以直接插入,但排序完畢後可能需要倒置連結串列;選擇排序比較次數一致,交換操作同樣比較麻煩。綜上,時間複雜度和空間複雜度並無明顯變化,若追求極致效能,氣泡排序的時間複雜度係數會變大,插入排序係數會減小,選