深度學習 --- 迴圈神經網路RNN詳解(BPTT)
今天開始深度學習的最後一個重量級的神經網路即RNN,這個網路在自然語言處理中用處很大,因此需要掌握它,同時本人打算在深度學習總結完成以後就開始自然語言處理的總結,至於強化學習呢,目前不打算總結了,因為我需要實戰已經總結完成的演算法,尤其是深度學習和自然語言的處理的實戰,所以大方向就這樣計劃。下面講講本節的內容,本節的的內容和以前一樣,從最初開始,慢慢探索到LSTM,廢話不多說下面開始:
RNN(Recurrent Neural Network),Jordan,Pineda.Williams,Elman等於上世紀80年代末末出的一種神經網路結構模型。這種網路的本質特徵是在處理單元之間既有內部的反饋連線又有前饋連線。從系統觀點看,它是一個反饋動力系統,在計算過程中體現過程動態特性,比前饋神經網路具有更強的動態行為和計算能力。迴圈神經網路現已成為國際上神經網路丏家研究的重要物件之一。
這種網路的內部狀態可以展示勱態時序行為。不同於前饋神經網路的是,RNN可以利用它內部的記憶來處理任意時序的輸入序列,這讓它可以更容易處理如不分段的手寫識別,語音識別等。在一個句子中,語意的分析和上下文很重要,因此需要考慮輸入的時間序列問題,因此很自然的想法就是延時在再輸入可以達到效果,下面我們看看RNN的經典結構:
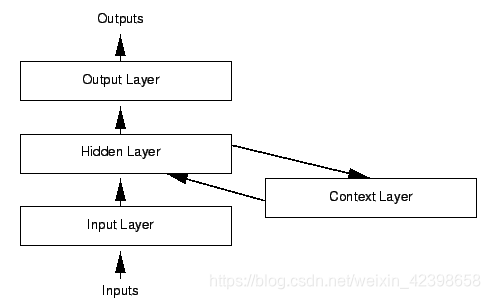
從上圖我們可以看出,若果沒有上下文層即Context Layer,則上面的網路就完全是一個標準的BP網路。如果加一個上文層就是迴圈神經網路了,加這一層的就是隱層的輸出延遲一個時間單元然後和隱層輸入一起再次輸入到隱層進行擬合,我們看看具體的神經網路如下:
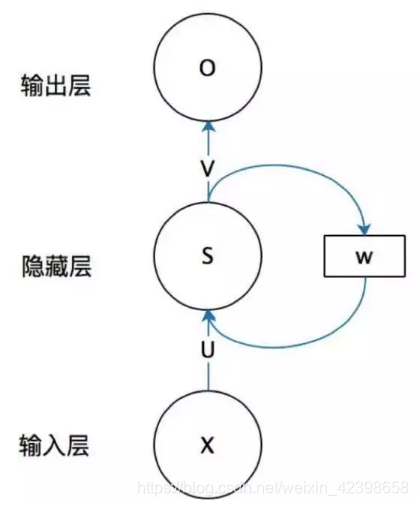
為了看清楚他們的資訊流向,這裡我們展開看看:
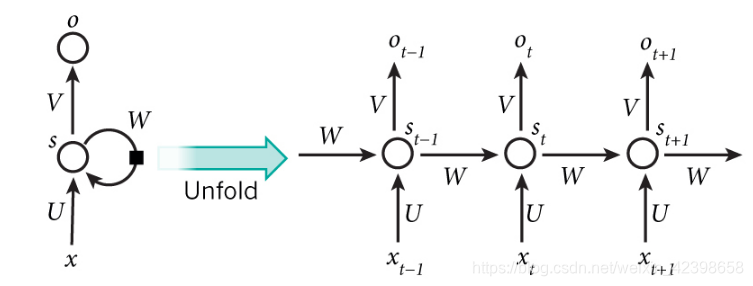
上圖的左邊是原始網路,右半部分為了觀察時間序列的是如何參與的,我們按照時間展開即t-1,t,t + 1,這裡大家需要搞明白什麼意思,在BP中的中間層稱為隱藏層,而在RNN裡稱為狀態層,其中ü代表輸入到隱層的權值,W代表返回的權值,V代表隱層輸出到輸出層的權值,我們知道BP的學習規則,而RNN是在BP的基礎上進行演變而來的,因此它的學習規則也是和BP很類似,只是稍微一點變化。學習演算法我們稍後介紹。下面簡單介紹一下埃爾曼神經網路。
Elman神經網路:
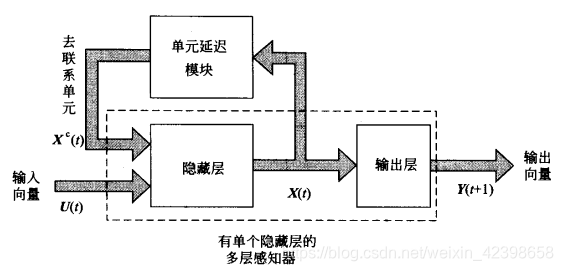
JLElman於1990年提出一種簡單的遞迴網路模型,如上圖所示該網路輸人層接受兩種訊號:一種是外加輸人;一種是來自隱層的反饋訊號
。將接受反饋的節點稱為聯絡單元(contextunit),
表示聯絡單元在時刻
的輸出;隱層輸出為
,為輸出
當輸出節點採用線性轉移函式時,有如下方程:
隱單元:
聯絡單元:
輸出單元:
還有一種遞迴神經網路NARX,也是很早就出現了,這裡就不詳細的介紹了,有興趣的可以自行查閱資料,下面我們看看RNN的訓練演算法BPTT(BackPropagation through Time)。
BPTT(通過時間反向傳播)
這裡先上圖,大家按照上面的圖對比理解:
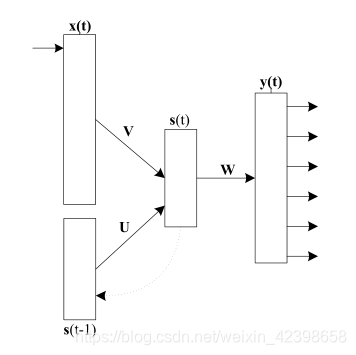
我們下面的就按照上圖進行講解訓練演算法,這裡先說明一下符號的意義:
| 神經元層 | 描述 | 下標變數 |
| |
輸入層 前一個隱藏(狀態)層 隱藏(狀態)層 輸出層 |
|
| 權值矩陣 | 描述 | 下標變數 |
| |
層輸入側 一個前隱藏層 層隱藏 |
|
層輸入側隱藏層:
(1)

這裡解釋一下,(1)式是說當前隱層狀態即噸時刻的狀態取決於啟用函式˚F和輸入的,而
有和當前輸入以及前一時刻的隱層輸出(此時前一時刻還包含好多前一時刻,隱層是時間的累加和即上式的紅色部分)同是加上偏置值。
層隱藏輸出層:
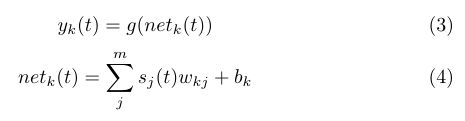
這是輸出層,同理和啟用函式克以及 決定,而
的是和隱層的多個神經元的和有關同時加上偏置值。
式上分別對應關係著啟用函式,而
就是待訓練的權值矩陣,下面我們就看看該網路的反向傳播學習演算法:
BP
下面構建我們的代價函式這裡取樣誤差平方和為代價函式。
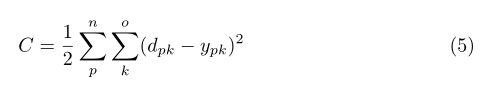
其中d是期望值,Y是網路的輸出值,下標p是代表的樣本個數,這裡為Ñ個樣本,這裡大家需要理清上面的噸是時間即前一個時間單位和後一個時間單位,這裡大家需要好好體會理解,還是簡單解釋一下,例如在自然語言處理中,我們的樣本就是很多的句子,而每個樣本即每個句子中又分為很多詞或者特徵,而我們輸入神經網路裡是按照一個詞一個詞(即一個維度)輸入進去的,因此有時間序列噸的概念。這裡大家需要理解一些,別暈了。搞清楚什麼是樣本,什麼是序列,什麼是維度,時刻想著這是序列的問題。為了讓大家搞明白我在舉個例子,例如公司的一年四個季度的收入情況,這裡呢,很多公司就是很多樣本,不同公司就是不同的樣本,而一個公司的的四個季度的收支情況就是時間序列(第一季度第二季度等等),而每個季度有三個月組成,那麼 三個月就是維度,即每個序列有三個維度,而我們輸入到神經元的是每個時間序列(首先輸入第一季度,然後是第二季度等等)而每個季度有3個維度即每個季度有三個月,因此對應三個神經元,下面畫出圖,大家結合圖還好理解他們的關係:
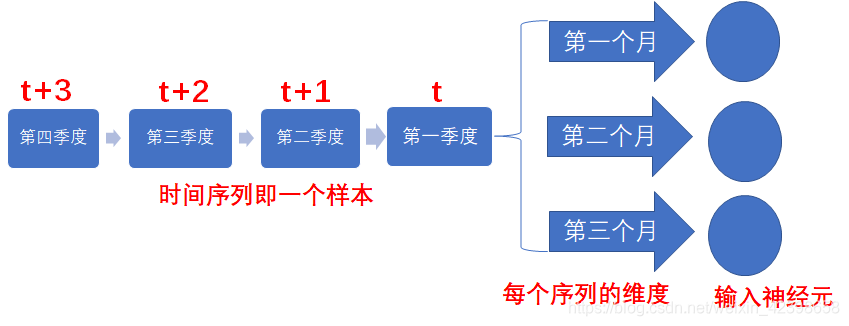
這裡大家結合剛開始的下標進行理解,我覺得理解應該沒問題了,那麼我們繼續往下講,下面就是我們最基本的BP了很簡單,這裡我把公式拿出來,簡單的敘述一下:

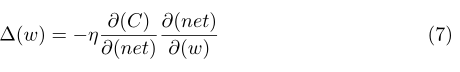
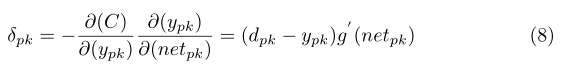
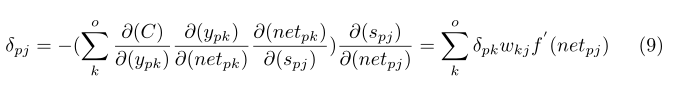
上面是很經典的BP反向傳播的計算公式,如果對此不理解或者感覺理解困難的同學說明你的基礎不紮實,請好好補一下BP的演算法推倒,推倒具體請檢視我的這篇文章,下面就看看三個權值更新:
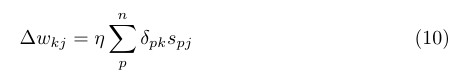

到這裡還是我們BP的反向傳播的演算法,這裡需要注意是以上都是針對當前時間序列也就是噸時刻,這裡唯一新一點的東西就是下式的ü權值的更新就是隱層的p個樣本對隱層的第j個神經元的誤差乘上上一個時刻隱層的神經元的輸出在乘上學習率就對U的調整了,這裡大家好好理解,我感覺都不難的,把BP該清楚還是很容易的。
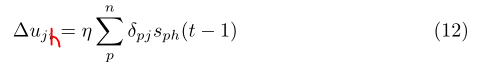
這就是權值更新的過程,但是該網路使用BP演算法的有什麼優缺點呢這裡我們開看看?
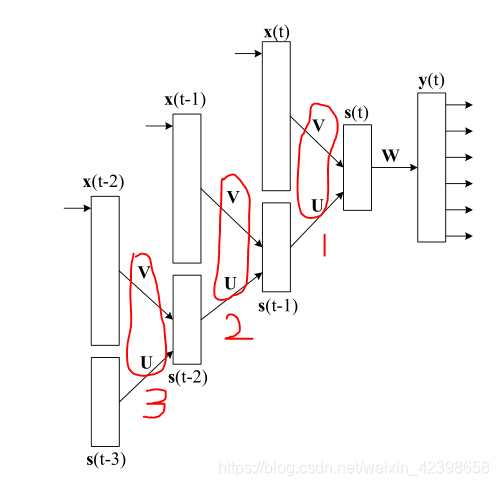
我們在看看(12)式,在更新ü時,需要他一上的時刻的值上面只用到這一層,但是
的值漢語中類似的依賴上一個
的值等等,這樣會有很多層,如上圖所示,但是我們怎麼更新這裡的權值ù和V呢?為了解決這個問題,引入了BPTT,我們下面就詳細的講講他是如何更新的,想要搞明白BPTT,上面的圖很關鍵,好下面我先使用口語化和大家解釋他是如何更新所有時間序列的權值的:
這裡我們先從輸出得到誤差訊號,反向傳播先更新W,更新完w ^後,誤差繼續向下傳播,更新然後的的U,V,即上圖的1標記層,然後誤差繼續沿著1標記反向傳播到
,然後更新2位置的U,V,此時問題就來了,如果我更新這裡的U,V那之前的1號位置的U,V還有效嗎?因為他們1,2,3 ,,,位置的U,V都是聯動的,即改變他們任何一個就會改變結果,所有我麼這裡要求只要改變2的U,V,那麼1,3 ,,等都會以相同的進行改變,現在在2號位置。然後全部改變,誤差繼續反向傳播到3的位置,開始改變U,V,同時其他的時序的U,V跟著相同的改變,然後繼續往下傳播,知道最後一層後,此時訓練結束了,權值的也就固定了,這就是BPTT的精髓了即時間不停的往前追溯直到剛開始的那個時間為止每追溯一層的權值都會統一根據本次的追溯進行調節權值U,V,直到追溯到剛開始的 時間。大家好好理解,但是這裡又有問題了,每次訓練都需要追溯到剛開始的時間嗎?通常情況是追溯到3到5層就足夠了,為什麼呢?因為追溯時間越多說明層數越多,那麼反向誤差面臨的梯度消失就會出現了,越往後U,V的改變數越小,因此一般3到5層就夠了下面給出BPTT的表示式:
根據第9式可推出下面的式子
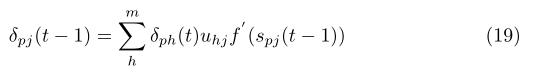
下面使用矩陣的形式給出BPTT的權值調整過程;
誤差訊號:

輸出權值調整寬:
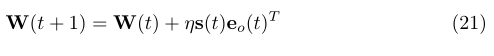
誤差從輸出層傳播到隱藏層:

d表示誤差訊號按單元計算得到。
![]()
權值V的更新:
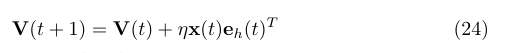
權值ü的更新;
![]()
上面就是權值的調整的向量化,下面給出BPTT遞迴更新的公式:
![]()
其中的英文追溯到時間的層數,如
說明追溯到第三層,圖產品上就是
的示意圖。
確定值以後就可以遞迴的呼叫U,V的權值呼叫公式了:
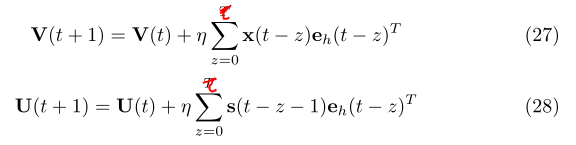
上面應該是,大家需要注意。
我們簡單的討論一下(26)式,他是說誤差訊號反向傳播到上一層,然後更新ü和V,因為每次的向上傳播都會更新其實就是U,V的累加,這裡大家需要理解這裡的累加為什麼?這就是BPTT算了。
好了,本節到此結束了,下一節我們探索BPTT的優缺點,根據缺點我們引入LSTM演算法解決了BPTT的缺點,下一節我們將詳細講解LSTM的工作原理。
本篇參考文獻為《BackPropagation Through Time》 Jiang Guo 2013.7.20
