選擇題

1.D 【解析】印表機屬於輸出裝置，它將一些資訊通過印表機打印出來。掃描器，鍵盤，滑鼠屬於輸入裝置。 2.D 【解析】 A，B，C選項的十進位制數值都是$617$，D選項的數值是$619$。 3.D 【解析】 $1MB=1024KB=1024×1024B$ 4.B 【解析】 廣域網的縮寫是$WAN$，區域網是$LAN$，都會網路是$MAN$。 5.B 【解析】 常識，要對資訊學競賽的背景有所瞭解。背景：1984年鄧小平指出：“計算機的普及要從娃娃做起。”中國計算機學會於1984年創辦全國青少年計算機程式設計競賽（簡 稱：NOI），當年參加競賽的有8000多人。 6.A 【解析】首先我們要知道CapsLock是鍵盤上用於切換大小寫得鍵。例如，你們來輸入的是小寫的a，如果你按了CapsLock鍵，輸出的就是大寫的$A$

A。模擬題目中的規矩，可以得到迴圈：$（A，S，D，F，a，s，d，f）$。其中每八個字母一個迴圈。$81 mod 8=1$，那麼輸出的就是迴圈節的第一個字元$A$。 7.A 【解析】 節點總數為：$k$⁰$+$$k$¹$+$…$+$$k$^h，接下來的問題就是如何化簡這個等比數列了。設$S=k$⁰$+$$k$¹$+$…$+$$k$^h，則$kS=k$¹$+$$k$²$+$…$+$$k$³，$kS-S=S(k-1)=k$^h+1$-1$,化簡一下就是$S$

=（kS=（k^h+1$-1）/（k-1）$。 8.A 【解析】 基數排序是根據每一個數位的大小進行排序的，類似於桶排序的思想。而氣泡排序，堆排序和直接插入排序都是基於比較的。 9.A 【解析】我們可以選用遞推的方法，設f[i]為i個數比大小的最小次數，$f[i]=f[i-2]+3,f[1]=0,f[2]=1$。含義就是對於每一組數，取兩個數比大小要$1$次，對於剩下的$i-2$個數要$f[i-2]$次，一次最大，一次最小，所以要$f[i-$

2]+1+2=f[i−2]+3f[i-2]+1+2=f[i-2]+3次，n=3-10的資料分別是$3,4,6,7,9,10,12,13$，帶入得A （好吧我也不是特別會） 10.B【解析】NOIP原題，不斷的出現重複和遞迴的結構十分相似。 11.A【解析】畫圖，略。 12.B【解析】對於我們所要求的S，相當於一個$10$位的二進位制位，$1$表示取，$0$表示不取，則共有$2$¹⁰$=256$種方案，或者暴力一點，$C(0,10)+C(1,10)+C(2,10)+...+C(10,10)=1024$,顯然這兩種方法都是可行的；對於T，顯然是10選7的組合數，即$C(7,10)=120$，那麼$T/S=120/1024=15/128$,選擇答案B。 13.B【解析】求10000的尤拉函式，根據唯一分解定理，$10000=2$⁴$*5$⁴,那麼就可以直接根據公式，$φ(10000)=10000×(1-1/2)×(1-1/5)=4000。$ 14.B【解析】樹狀陣列$lowbit$運算，求二進位制位有多少個$1$。當然考場上最簡單的方法莫過於帶一個數進去了，算完後就知道ACD算不出答案。 15.B【解析】結構類似於桶，先進後出，屬於資料結構棧。

問題求解

第一題.去了 沒去 沒去 沒下雨 【解析】 從中我們知道一個規律，如果$AB$都成立那麼$C$成立，若C不成立，A和B中有一個成立的時候另一個便不成立。 因為丙去了，根據已知$③$可知丁不去。 根據$④$，如果丁和甲同時不去，說明丙也不能去，而因為丁去了，只有讓甲去丙才能不去。 根據$②$，如果乙去則丁去，當丁沒去說明乙也沒有去。 根據$①$，如果下雨且乙不去那麼甲也不去，而乙去了，甲卻沒去，說明沒有下雨。 我們要根據已知去推，這也是一道比較簡單的邏輯題了。 第二題.$544$ 【解析】 我們從位數去考慮。 1位數：$1$個。只有一個數字$8$. 2位數：如果十位$1,2,3,4,5,6,7,9$，那麼有$8$個（後面都接上1位的方案數）；如果十位是$8$，則有$10$個數字（$8$後接任意陣列均可）。共有$8+10=18$（個） 3位數：如果百位$1,2,3,4,5,6,7,9$，那麼有面可以跟個位有數字$8$的（如$108$），也可以跟十位有陣列$8$的（如$188$），共$8×(1+18)=152$種；若百位是$8$，有$100$種方案。共有$152+100=252$（個） 4位數：$1$開頭有$1+18+252=271$（個）；$2$開頭有$2008,2018$，共$2$個；共有$271+2=273$個。 共計：$1+18+252+273=544$（個）

閱讀程式寫結果

1.$RuanHuoMianTai$ 【解析】程式的左右是掃描字串的每一個字元，使得每一個大寫字母ASC碼+1，或者變成剛剛比它大1（或後面）的大寫字母。 2.$4$ 【解析】程式的作用是從1-14種尋著是否存在數i，使得$i$² $mod 15=1$(或$i$² %$15=1$),通過手動計算不難發現滿足條件的數字是$1,4,6,14$；共計$4$個數，因此答案是$4$。 3.$8$ 【解析】這是一道遞迴的計算題，如果直接這麼做顯然顯得麻煩了。因此我們可以通過畫二維表的方式來求解這個答案。 對於第0行，其大小為該縱座標。 對於第0列，其大小為該橫座標對於3取模的值。 對於任何一個非0座標，其大小為上面的數值加上左上角的數值減去左邊的數值。 我們可以採用遞推的方法解決。 4.$6$ 【解析】這道題就是一個模擬連結串列的過程，查詢有多少個聯通快。仔細模擬，發現是6個。

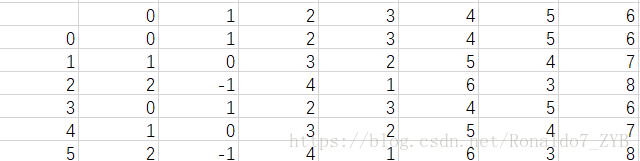
完善程式

1.最大公約數之和 答案：i * i; n/i; return a; a%b; ans+gcd(a[i],b[i]) 【解析】 題目的過程就是先找到所有的因數，再進行累加。 我們首先看第一段，有一個函式的名稱叫做getDivisor，其實就是求解每一個n的因子。 依照題意，時間複雜度是（Osqrt(n)）,那麼我們在每一因子i的時候就是1-sqrt（n）這個區間來列舉的。對於最大情況，只有i * i=n,超過就不滿足時間複雜度和列舉的要求了，因此第一空所填的就是i * i。當列舉的時候如果這個數是i的因子那麼就接著統計。以36為例，i是從1-6來列舉的，如果列舉到2，那麼因子18就是通過36/2，或者是n/i來得到；特別的，當i=6的時候，不需要操作，此時n=i*i,即n/i=i時不需要進行操作，所有第二空所填的是n/i。需要注意，儘管使用sqrt函式仍然屬於等價寫法，但是程式中並沒有載入cmath庫，因此這麼寫是錯誤的。 再看求去最大公因數的過程gcd，這就是一個模擬輾轉相除法的過程。複雜度是O（logMAXAB）級別的，因此不要寫成是輾轉相減法。如果餘數是0就返回a，那麼第三空就是return a；否則繼續取模，因此第四空是a%b。 接下來就是累加答案，累加每一個質因子即可，存在ans上面。因此第五空是ans+gcd(a[i],a[j])。 2.連結串列 答案：a[x]=i;i+1;R[a[i]];a[i];R[i] 【解析1】套路法（分數8-14） 空1：唯一可行的兩個答案a[i]=x和a[x]=i，若是前者可直接cin>>a[i]代替，故答案為後者。 空2：L是i-1，那麼R是指向右節點的，上下符號相反，必然是i+1 空3/4：上下文對稱，L和R恰好反一下。例如第一句是L[R[a[i]]]=L[a[i]];第二句是R[L[a[i]]]=R[a[i]],根據雙向連結串列的對稱性很容易得到答案。 空5：套中套，很多人想到的是R[a[i]]，符合上文的結構，但是陰險的出題人一定會在最後一個空坑你一把，只讓你輸出最簡單的R[i],你也可以考試的時候推一下。 【解析2】理解演算法含義 第一空是標記每一個x出現的位置； 第二空雙向連結串列R指向後面的元素，即i+1； 三四空是用於刪除元素，這是連結串列最基本的刪除操作，可以自行理解資料結構的實現； 第五空主要是輸出每一個元素的答案，但是要按照輸入的順序進行輸出因此要R[i]而不是R[a[i]],否則就按照了大小的順序輸出了。

本人預估浙江分數線85上下 （不要14年那麼恐怖就好） 浙江學子依舊生活在水深火熱之中… 能在考場上拿到90分已經是很滿意了。 若有疏忽或者意見望大家指正。