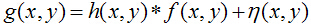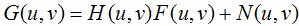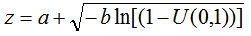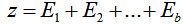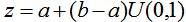1.研究噪聲特性的必要性

        本文的內容主要介紹了常見噪聲的分類與其特性。將噪聲建模，然後用模型去實現各式各樣的噪聲。

        實際生活中的各種照片的老化，都可以歸結為以下老化模型。

     這個模型很簡單，也可以直接用以下公式來表達。

在頻域內，用以下公式區表示。

     根據以上式子，可以看出，老舊照片的復原，主要分為兩個任務，一個是去噪；另一個是去卷積，或者稱為逆濾波，也就是將老化濾波器做反處理。

     本文首先由噪聲型別與其建模。隨後的博文，會介紹幾種基礎的去噪方法和基礎的逆濾波方法。

2.噪聲的實現

      2.1    評價用影象與其直方圖

        

      2.2  高斯噪聲

        高斯噪聲，也稱為正態噪聲，其統計特性服從正態分佈。一種較為泛用的噪聲模型。          Matlab的實現較為簡單，Matlab已經有一個randn(M,N)的函式，用其可以產生出均值為0、方差為1、尺寸為M X N畫素的高斯噪聲影象。         用以下程式就可以產生任意均值和方差的高斯噪聲。

a = 0;
b = 0.08;
n_gaussian = a + b .* randn(M,N);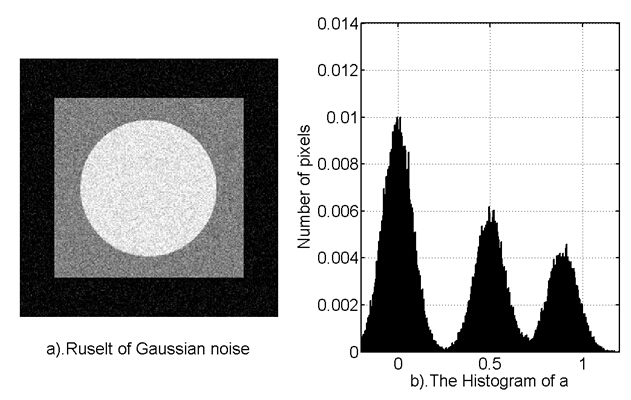

         

        2.3 瑞利噪聲

        瑞利噪聲相比高斯噪聲而言，其形狀向右歪斜，這對於擬合某些歪斜直方圖噪聲很有用。

        瑞利噪聲的實現可以藉由平均噪聲來實現。如下所示。

這裡的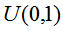表示均值為0，方差為1的均勻分佈的噪聲。Matlab裡，使用函式rand(M,N)就可以產生一個均值為0，方差為1的均勻噪聲。

a = -0.2;
b = 0.03;
n_rayleigh = a + (-b .* log(1 - rand(M,N))).^0.5;

        

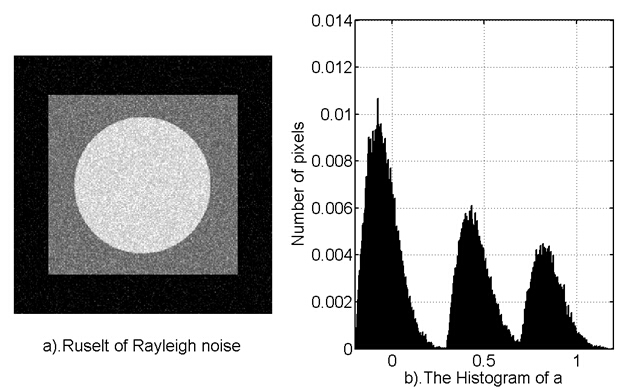
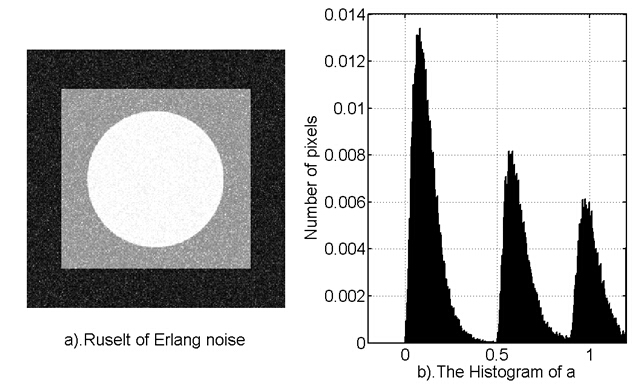
       2.4 伽馬噪聲

         伽馬噪聲的分佈，服從了伽馬曲線的分佈。伽馬噪聲的實現，需要使用b個服從指數分佈的噪聲疊加而來。指數分佈的噪聲，可以使用均勻分佈來實現。

使用若干個(這裡用b表示)均勻分佈疊加，就可以得到伽馬噪聲。

當然，當b=1的時候，就可以得到指數噪聲了。

a = 25;
b = 3;
n_Erlang = zeros(M,N); 
for j=1:b
    n_Erlang = n_Erlang + (-1/a)*log(1 - rand(M,N));
end

         2.5 均勻噪聲

             如同前面所示，均勻噪聲可以由函式rand(M,N)直接產生。

a = 0;
b = 0.3;
n_Uniform = a + (b-a)*rand(M,N);

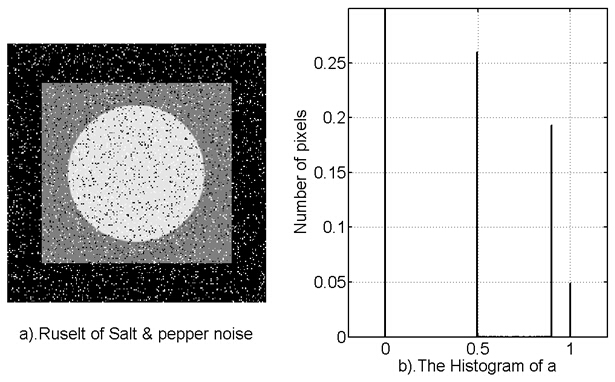
         2.6 椒鹽噪聲

         椒鹽噪聲也成為雙脈衝噪聲。在早期的印刷電影膠片上，由於膠片化學性質的不穩定和播放時候的損傷，會使得膠片表面的感光材料和膠片的基底欠落，在播放時候，產生一些或白或黑的損傷。事實上，這也可以歸結為特殊的椒鹽噪聲。

        椒鹽噪聲的實現，需要一些邏輯判斷。這裡我們的思路是，產生均勻噪聲，然後將超過閾值的點設定為黑點，或白點。當然，如果需要擬合電影膠片的損傷的話，可以選用別的型別噪聲去擬合。

a = 0.05;
b = 0.05;
x = rand(M,N);
g_sp = zeros(M,N);
g_sp = f;
g_sp(find(x<=a)) = 0;
g_sp(find(x > a & x<(a+b))) = 1;

3.總結

     本文，實現的幾類較為基本的噪聲。並給出了其實現的方法，程式碼在下面。下一篇博文，會進行幾個常用去噪濾波器的比較。

close all;
clear all;
clc;
f = imread('./original_pattern.tif');
f = mat2gray(f,[0 255]);
[M,N] = size(f);
figure();
subplot(1,2,1);
imshow(f,[0 1]);
xlabel('a).Original image');
subplot(1,2,2);
x = linspace(-0.2,1.2,358);
h = hist(f,x)/(M*N);
Histogram = zeros(358,1);
for y = 1:256
    Histogram = Histogram + h(:,y);
end
bar(-0.2:1/255:1.2,Histogram);
axis([-0.2 1.2 0 0.014]),grid;
xlabel('b).The Histogram of a');
ylabel('Number of pixels');
%% ---------------gaussian-------------------
a = 0;
b = 0.08;
n_gaussian = a + b .* randn(M,N);
g_gaussian = f + n_gaussian; 
figure();
subplot(1,2,1);
imshow(g_gaussian,[0 1]);
xlabel('a).Ruselt of Gaussian noise');
subplot(1,2,2);
x = linspace(-0.2,1.2,358);
h = hist(g_gaussian,x)/(M*N);
Histogram = zeros(358,1);
for y = 1:256
    Histogram = Histogram + h(:,y);
end
bar(-0.2:1/255:1.2,Histogram);
axis([-0.2 1.2 0 0.014]),grid;
xlabel('b).The Histogram of a');
ylabel('Number of pixels');
%% ---------------rayleigh-------------------
a = -0.2;
b = 0.03;
n_rayleigh = a + (-b .* log(1 - rand(M,N))).^0.5;
g_rayleigh = f + n_rayleigh; 
figure();
subplot(1,2,1);
imshow(g_rayleigh,[0 1]);
xlabel('a).Ruselt of Rayleigh noise');
subplot(1,2,2);
x = linspace(-0.2,1.2,358);
h = hist(g_rayleigh,x)/(M*N);
Histogram = zeros(358,1);
for y = 1:256
    Histogram = Histogram + h(:,y);
end
bar(-0.2:1/255:1.2,Histogram);
axis([-0.2 1.2 0 0.014]),grid;
xlabel('b).The Histogram of a');
ylabel('Number of pixels');
%% ---------------Erlang-------------------
a = 25;
b = 3;
n_Erlang = zeros(M,N); 
for j=1:b
    n_Erlang = n_Erlang + (-1/a)*log(1 - rand(M,N));
end
g_Erlang = f + n_Erlang; 
figure();
subplot(1,2,1);
imshow(g_Erlang,[0 1]);
xlabel('a).Ruselt of Erlang noise');
subplot(1,2,2);
x = linspace(-0.2,1.2,358);
h = hist(g_Erlang,x)/(M*N);
Histogram = zeros(358,1);
for y = 1:256
    Histogram = Histogram + h(:,y);
end
bar(-0.2:1/255:1.2,Histogram);
axis([-0.2 1.2 0 0.014]),grid;
xlabel('b).The Histogram of a');
ylabel('Number of pixels');
%% ---------------Exponential-------------------
a = 9;
n_Ex = (-1/a)*log(1 - rand(M,N)); 
g_Ex = f + n_Ex;
figure();
subplot(1,2,1);
imshow(g_Ex,[0 1]);
xlabel('a).Ruselt of Exponential noise');
subplot(1,2,2);
x = linspace(-0.2,1.2,358);
h = hist(g_Ex,x)/(M*N);
Histogram = zeros(358,1);
for y = 1:256
    Histogram = Histogram + h(:,y);
end
bar(-0.2:1/255:1.2,Histogram);
axis([-0.2 1.2 0 0.014]),grid;
xlabel('b).The Histogram of a');
ylabel('Number of pixels');
%% ---------------Uniform-------------------
a = 0;
b = 0.3;
n_Uniform = a + (b-a)*rand(M,N);
g_Uniform = f + n_Uniform;
figure();
subplot(1,2,1);
imshow(g_Uniform,[0 1]);
xlabel('a).Ruselt of Uniform noise');
subplot(1,2,2);
x = linspace(-0.2,1.2,358);
h = hist(g_Uniform,x)/(M*N);
Histogram = zeros(358,1);
for y = 1:256
    Histogram = Histogram + h(:,y);
end
bar(-0.2:1/255:1.2,Histogram);
axis([-0.2 1.2 0 0.014]),grid;
xlabel('b).The Histogram of a');
ylabel('Number of pixels');
%% ---------------Salt & pepper-------------------
a = 0.05;
b = 0.05;
x = rand(M,N);
g_sp = zeros(M,N);
g_sp = f;
g_sp(find(x<=a)) = 0;
g_sp(find(x > a & x<(a+b))) = 1;
figure();
subplot(1,2,1);
imshow(g_sp,[0 1]);
xlabel('a).Ruselt of Salt & pepper noise');
subplot(1,2,2);
x = linspace(-0.2,1.2,358);
h = hist(g_sp,x)/(M*N);
Histogram = zeros(358,1);
for y = 1:256
    Histogram = Histogram + h(:,y);
end
bar(-0.2:1/255:1.2,Histogram);
axis([-0.2 1.2 0 0.3]),grid;
xlabel('b).The Histogram of a');
ylabel('Number of pixels');