蓋爾-沙普利[Gale-Shapley]婚姻穩定匹配演算法

1 背景說明

   蓋爾-沙普利(Gale-Shapley)穩定匹配演算法是美國數學家 David Gale 和 Lloyd Shapley在1962年提出的一種尋找穩定婚姻的策略。這種匹配方式的特點在於：不管需要匹配的總人數有多少、不管他們各自的偏好如何，只要男女人數相等，並且男女雙方每個人都能在心中給對方打分，那麼應用這種策略後總能得到一個穩定的婚姻搭配。換句話說，他們證明了穩定的婚姻搭配總是存在的。並且這種策略反映了現實生活中的很多真實情況，也不僅僅侷限於婚姻匹配。

2 原理及思路

2.1 問題的描述

   現在，讓我們來更加仔細地描述這個問題。

   有N男N女需要尋找結婚物件，並假設他們的性取向全部正常——即婚姻的搭配方式只有男&女這一種。要求是幫助這N男N女中的每個人都成功匹配一個婚姻的物件，並且這個物件必須是穩定的。

   什麼是穩定呢？舉個例子說明：

   假設有兩對夫妻M1&F2、M2&F1。M1心中更喜歡F1，但是他和F2結婚了，M2心目中更喜歡F2，但是他和F1結婚了，顯然這樣的婚姻是不穩定的，因為隨時都可能發生M1和F1私奔或者M2和F2私奔的情況(當然，在這裡我們需要假設情感因素是婚姻絕對的主導，雖然這在生活中基本不存在，但是在數學世界中我們不妨就這麼假設)。所以在男女雙方做匹配時(也就是結婚的時候)需要做出穩定的選擇，以防這種情況的發生。

   (PS：博主還很年輕，為了方面我的描述，我下面還是把所有“結婚”描述為“戀愛”好了，勿怪,勿怪~。)

2.2 蓋爾-沙普利演算法的思路

   蓋爾-沙普利(Gale-Shapley)穩定匹配演算法解決了這一問題，它的思路如下。

   首先，男生需要按照希望與之交往的順序給所有女生排序，即最理想的女友排在最前、最不理想的放在最後。同樣，每個女生也需要給男生排序。接著，男生將按照自己的名單一輪一輪地去追求喜歡的女生，女生也將按照自己的名單接受或拒絕對方的追求。

   第一輪，每個男生都向自己名單上排在首位的女生表白。此時，一個女生可能面對的情況有三種：沒有人跟她表白、只有一人跟她表白、有不止一人跟她表白。在第一種情況下，這個女生什麼都不做，繼續等待即可；在第二種情況下，女生接受那個人的表白，答應暫時和他做男女朋友；在第三種情況下，女生從所有追求者中選擇自己最喜歡的那一位，答應和他暫時做男女朋友，並拒絕其他所有的追求者。

   第一輪結束後，有些男生已經有女朋友了而有些男生仍然是單身狗。在第二輪表白行動中，每個單身男都會從所有還沒拒絕過自己的女生中選出自己最喜歡的那一個，並向她表白，不管她現在是否是單身。和第一輪一樣，每個被表白的女生需要從表白者中選擇最喜歡的男生，並拒絕其他追求者。注意，如果這個女生當前已經有男朋友了，當她遇到了更好的追求者時，她將毫不猶豫地和現男友分手，投向新追求者的懷抱。這樣以來，一些單身狗將脫單，而一些倒黴的恩愛狗（男）也會被分手，重新進入單身狗的行列。

   在以後的每一輪中，單身狗們將發揚愈挫愈勇的頑強精神，繼續追求列表中的下一個女生；女生則從包括現男友在內的所有追求者中選擇最好的一個，並給其他所有追求者發好人卡。這樣一輪一輪地進行下去，直到某個時刻所有人都不再單身，那麼下一輪將不會有任何新的表白，每個人的物件也都將固定下來，整個過程自動結束——此時的搭配就一定是穩定的了。

3 程式實現

   在弄明白了原理後，寫程式碼其實是最簡單的一步。我是用MATLAB寫的，不過對於這樣一個簡單的演算法來說用MATLAB寫還是用C或者一些其他什麼語言寫基本沒多少差距，可能唯一的不同就是自己的熟練度了。

   我的核心程式碼是一個while迴圈，內部分為2個部分：男生追求(M:courtship)和女生回覆(F:response)。其中男生追求的程式碼是長這個樣子的：

% M: courtship
    for i=1:Num                                 % 對於每個男生
        if M_sg(i)==1                           % 如果他當前是單身
            for j=1:Num                         % 就按喜歡程度從高到低給每位女生排序(不管女生是否單身)
                if M(i,j)~=0                    % 選擇沒有拒絕過自己的女生中最喜歡的那一個
                    for k=1: Num                % 發出情書
                        if F(M(i,j),k)==i
                            F_mark(M(i,j),k)=1;
                            break;
                        end
                    end
                    break;
                end
            end
        end
    end

   而女生回覆的程式碼是長這個樣子的：

% F: response
    for i=1:Num                         
        if sum(F_mark(i,:)~=0)                          % 每個收到情書的女生(不論是否單身)
            for j=1:Num
                
                if F_mark(i,j)==1                       % 只接受其中最喜歡的男生的情書
                    F_cp(i)=F(i,j);                     % 於是這個女生有了CP
                    M_cp(F(i,j))=i;                     % 對應的男生也有了CP
                    M_sg(F(i,j))=0;                     % 同時，那個男生摘掉了單身狗的帽子
                    if j<Num                            % 如果女生接受的情書不來自於自己最不喜歡的男生，即對更不喜歡的男生有拒絕權
                        for k=j+1:Num                   % 則檢視更不喜歡的男生(們)——很可能不止一個——是否發來了情書
                            if F_mark(i,k)==1           % 若有
                                F_mark(i,k)=0;          % 那麼首先扔掉該男生髮來的情書(包括之前的情書，即現男友的情書)
                                for s=1:Num             
                                    if M(F(i,k),s)==i
                                        M(F(i,k),s)=0;  % 然後給該男生髮一張好人卡(或和現男友分手)
                                        M_sg(F(i,k))=1; % 於是該男生重新回到單身狗的行列
                                        break;
                                    end
                                end
                            end
                        end
                    end
                    break;
                end
            end
        else
            continue;                   % 先暫時跳過沒收到情書的女生
        end
    end

   上面這兩段程式碼是這個演算法的核心內容，看上去是不是so easy？讀者如果想試一試，只要把它們連在一起套在一個while裡就好了，當然別忘了定義一些程式碼裡出現過的變數之類的準備工作。這裡比較繞人的是於二維陣列的應用，需要仔細對照陣列的下標，什麼i、j、k、s可千萬別弄錯了。至於其他的部分，我也利用了MATLAB的便利繪製了一些圖片作比較和分析，下面我會講到的。

4 結果分析

   在付出了一個下午的辛勤勞動後，程式碼終於寫出來並調通了。下面將簡單介紹程式執行的結果並作簡要分析。

   首先展示的是100對男生女生的匹配結果，如圖1所示：

     圖中藍色小點的縱座標表示男生最終追到的女生在自己列表上的排名，排名數字越小，表示該男生對現女友越喜愛，即當前的女友越接近自己的最愛。紅點代表女生，所代表的意義和藍點是一樣的，即紅色小點的縱座標表示女生最終接受的男友在自己列表上的排名。橫座標的人數實際上是“男女生對數”，因此每個橫座標上有2個數據點，紅、藍各一。

   再仔細地看這張圖我們會發現在發多數情況下藍色小點處於其相對應的紅色小點的下方。很明顯：男生找到的伴侶離自己的最愛比女生更近——而且還不止一點點！也就是說，在這種策略下，男生更容易收穫自己的女神而女神則非常難獲得自己的男神。

   為了更清晰地表現這一結論，我製作了下方的圖2。其中橫座標表示男女匹配的輪數，縱座標表示在該輪匹配結束後，100名男生女生的物件在自己列表中排名的平均值(注:當前為單身的男生女生不計)。

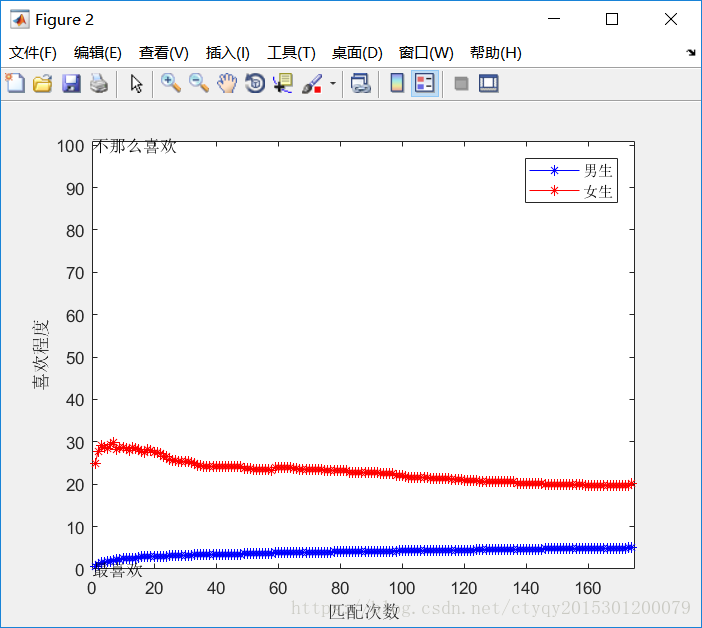
     圖中藍色表示男生，紅色表示女生，橫座標為匹配輪數，縱座標為該輪數完成後對當前物件的平均喜愛程度：縱座標為排名，數值越小喜愛程度越高。

   從圖中明顯可以看出：男生對自己的女友的平均喜愛程度大大高於女生對自己男友的平均喜愛程度。隨著匹配輪數的增加，男生對女友的喜愛程度逐漸下降至平穩，女生對自己男友喜愛程度逐漸上升至平穩；而且在第一輪時非單身的男生總的找到自己的“女神”，即最喜愛的女生作為女友。這是由於每次總是男生主動追求，所以在第一輪時，對所有男生來說，只要能匹配到女友，那麼該女友就一定是自己的最愛。當然了，在後續的匹配輪中男生也很可能失去自己的女神——除非女神最愛的男生恰好也是自己——然而這種概率並不大。而在後續匹配中，由於仍然是男生主動追求，女生只能在追求自己的人中挑選，所以女生對男友的滿意程度總是比不上男生對女友的滿意程度——畢竟每個男生都有機會追求自己的女神，而對很多女生來說，直到匹配結束也等不到自己男神的表白。

   為了使模擬更加貼近現實，我們不妨設定有1000對男女參與匹配。結果如圖3和圖4所示。

     這次一共為1000對男女匹配了1838輪，最終得到了穩定的匹配結果。結果更加直觀了，圖3藍色幾乎排成一條直線，並且大部分都處在[0,20]區間內，而代表女生的紅點則分佈得很分散，雖然總地來說呈現“下密上疏”的狀態但是遠遠無法和男生相比。

   同樣地，喜愛程度隨輪數而變化的規律也更加明顯。在得到穩定匹配後，男生對女友的平均喜愛程度得分為8.4，而女生的得分為123。因此我們不妨這麼認為，在得到穩定匹配後，男生最終獲得的女友是男生的喜愛列表上的第8或第9位女生，而女生最終獲得的男友則是女生的喜愛列表上的第123位男生（男生女生的喜愛列表上各自有1000名異性的名字），這樣看來說是天壤之別也不為過了。

   同樣的策略也可以用來分析其他類似的互選過程，比如校園招聘。在校招時，經過對所有提交簡歷的學生的考察和排序，招聘方給列表上的前若干名學生髮出邀請；而每個學生也都會得到一份或多份邀請（請自行忽略沒有收到邀請的學生和沒有收到簡歷的招聘方，或假設這種情況不存在），學生選擇最好的一個並拒絕其他的offer，招聘方在得到第一輪反饋後劃掉拒絕自己的學生，並從wait list 中增補所缺名額。這樣一輪輪地互選直到雙方都滿意，那麼也就達成了最穩定匹配。在這種情況下，招聘方扮演了男生的角色，而學生則扮演了女生的角色。因此我們可以看到，每年校招時，招聘公司總能招到儘可能優秀的學生，而學生卻往往比較難獲得最心儀的offer。

   還有個比較相似的例子就是高考填志願。填志願是考生和學校的互選，不妨就把考生的志願表看作是上文中男生的“女友列表”，學校在收到考生的“表白”後，會給最好的那一部分發錄取通知，相當於上文中的女孩接受了男生的“表白”。而對於沒有被錄取的學生，系統會將他志願表上稍次一點的選項傳送給對應的學校（男生被當前女生拒絕，向下一位女生表白），而稍次一點的學校也會進行同樣的選擇。這樣反覆匹配直至完成。而當學生給志願表上所有學校都發了入學申請卻都遭遇拒絕時，這名學生就會被“退檔”，如本一直接轉為本二。這在現實生活中是存在的，每個高校的每個專業都會設定一定的退檔率，如1:1.05等，設定這樣一個規則的原因是學校希望能找到儘可能優秀的學生，也是為了在某種程度上彌補學校因作為上文中的“女生”一方而天然受到的限制。

5 後記

   最後需要說明的是，現實生活中的匹配當然不會如本文所描述得那樣一絲不苟，但即使如此，這種策略所反映的結果卻和生活經驗高度吻合。如果說還能有什麼啟示，那就是：

   大膽去愛吧！不論是男生還是女生，主動追求永遠比被動等待更有希望獲得幸福。

   程式碼已上傳至網路，點選連結下載，密碼是spn2。