Given a linked list, return the node where the cycle begins. If there is no cycle, return null.

Note: Do not modify the linked list.

Follow up: Can you solve it without using extra space?

給定一個連結串列，返回連結串列開始入環的第一個節點。 如果連結串列無環，則返回 null。

說明：不允許修改給定的連結串列。

進階： 你是否可以不用額外空間解決此題？

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
        if (head == null || head.next == null)  return null;
        ListNode runner = head;
        ListNode walker = head;
        while (runner.next != null && runner.next.next != null) {
            walker = walker.next;
            runner = runner.next.next;
            if (walker == runner) {
                ListNode walker2 = head;
                while (walker != walker2) {
                    walker = walker.next;
                    walker2 = walker2.next;
                }
                return walker; // 考慮只有一個結點自環，不能在第二個while裡面判斷
            }
        }
        return null;
    }
}
 

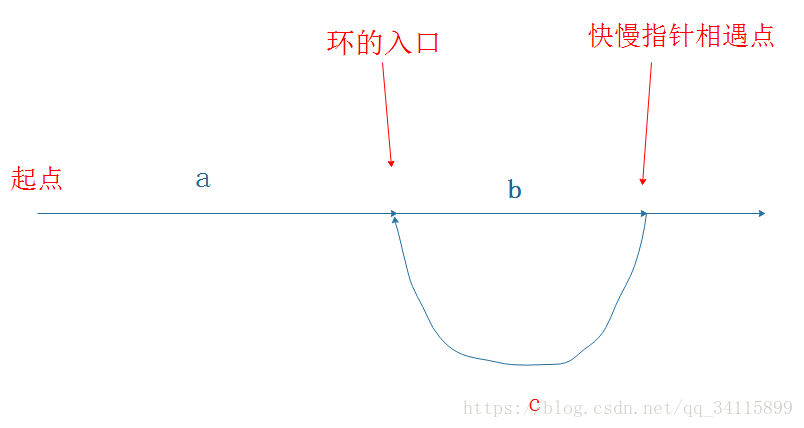
原因分析：為什麼快慢指標在相遇點時再設定一個指標從頭開始慢走，然後第二個指標在環裡慢走，再次相遇就是入口點呢？

當它遇到慢速指標walker時，快速指標runner可能會執行幾個圓而不是一個圓。

假設快速指標runner執行m個圓圈，並在它們相遇時慢速指標walker執行n個圓圈。然後我們可以得到如下結論：

runner走的距離  =   walker走的距離的幾倍，假設是L倍！顯然L > 1，因為runner走的一定比walker遠

a + m *（b + c）+ b = L * (a + n *（b + c）+ b)

因此我們化簡可以得到： m*b + m*c =  (L-1)*a +（L*n+L-1)*b + L*n*c 

有兩種可能性：

待定係數法，以b為準

m=L*n+L-1  -------①

m=a/c(L-1) + L*n   -------②

由①②得出

L-1=a/c(L-1)

而L>1，所以a=c成立，所以在快慢指標相遇點再設定一個指標從頭開始慢走，然後第二個指標在環裡慢走，再次相遇就是入口點

待定係數法，以c為準

m=L*n                     -------------①

m=L*n+L-1+a/b(L-1)       ------------②

由①②得出

1-L=a/b(L-1)

L>1,所以a=-b，而距離不可能是負數，所以這種情況不成立！

綜上所述，a=c成立

那麼，我們只需要在快慢指標相遇點再次設定一個指標從頭開始走，在環裡的慢指標只走一輪就可以和從頭到環的入口點的指標相遇。於是就有了如下部分的程式碼：

            if (walker == runner) {
                ListNode walker2 = head;
                while (walker != walker2) {
                    walker = walker.next;
                    walker2 = walker2.next;
                }
                return walker; // 考慮只有一個結點自環，不能在第二個while裡面判斷
            }

=========================Talk is cheap, show me the code========================