前言

日常開發中位運算不是很常用，但是巧妙的使用位運算可以大量減少執行開銷，優化演算法。舉個例子，翻轉操作比較常見，比如初始值為1，操作一次變為0，再操作一次變為1。可能的做法是使用三木運算子，判斷原始值為1還是0，如果是1，設定為0，否則設定為0.但是使用位運算，不用判斷原始值，直接改變值就可以：

1^num//num為原始值

當然，一條語句可能對程式碼沒什麼影響，但是在高重複，大資料量的情況下將會節省很多開銷。

以下是關於java位運算的部分內容，如有錯誤，還請指出，以共同進步，先行致謝。

1. 位運算子

1.1 java支援的位運算子：

&：按位與。

|：按位或。

~：按位非。

^：按位異或。

<<：左位移運算子。

>>：右位移運算子。

<<<：無符號右移運算子。

位運 算 符 中 ,除 ～ 以 外 ,其餘 均 為 二 元 運 算 符 。 操 作 數 只 能 為 整 型 和字 符 型 數 據 。

Java使用 補 碼 來 表 示 二 進 制 數 ,在補 碼 表 示 中 ,最高 位 為 符號 位 ,正數 的 符 號 位 為 0,負數 為 1。補 碼 的 規 定 如 下 :

對 正 數 來 說 ,最高位為 0,其餘 各 位 代 表 數 值 本 身 (以二 進位制 表 示 ),如 +42的補碼 為 00101010。

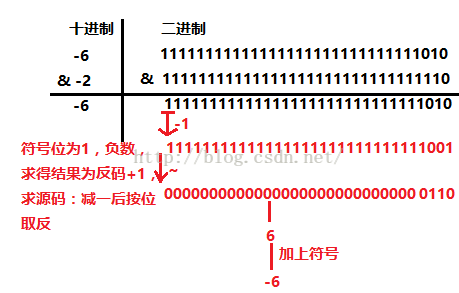
對 負 數 而 言 ,把該 數 絕 對 值 的 補 碼 按 位 取 反 ,然後 對 整 個數 加 1,即得 該 數的 補 碼 。 如 -1的補 碼 為11111111111111111111111111111111(00000000000000000000000000000001按 位 取 反 11111111111111111111111111111110+1=11111111111111111111111111111111 )。為何有那麼多0、1，java中int是32位的。

1.2   按位與（&）

按位與的運算規則

規則總結：只有兩個運算元對應位同為1時，結果為1，其餘全為0. （或者是隻要有一個運算元為0，結果就為0）。

舉例：

1.3 按位或（|）

按位或的運算規則

規則總結：只有兩個運算元對應位同為0時，結果為0，其餘全為1.（或者是隻要有一個運算元為1，結果就為1）。

1.4按位非（~）

按位非的運算規則

在求負數的原始碼中使用過。

1.5 按位異或（^）

按位異或的運算規則

規則總結：異：1.

1.6 左位移（<<）

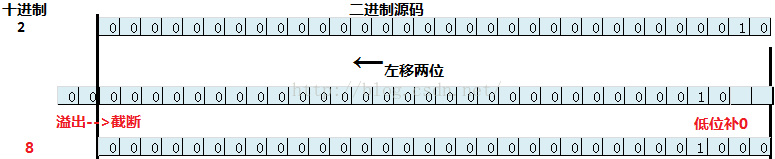
算術右移（>>）: 符號位不變，低位補0。如：2<<2結果為8。

當移動的位數超過數字本身的位數時，那麼不就都需要補0操作，實際上不是的，java不可能做那麼浪費資源的事情。在真正執行位移前，其對要移動的位數做了一些預處理，比如32處理為0，-1處理為31.

1.7 右位移（>>）

低位溢位，符號位不變，並用符號位補溢位的高位。如：-6>>2結果為-2。

1.8 無符號右移（>>>）

低位溢位，高位補0。注意，無符號右移（>>>）中的符號位（最高位）也跟著變，無符號的意思是將符號位當作數字位看待。如：-1>>>1結果為2147483647。這個數字應該比較熟悉，看兩個輸出語句就知道是什麼了：

System.out.println(Integer.toBinaryString(-1>>>1));

System.out.println(Integer.toBinaryString(Integer.MAX_VALUE));

輸出結果為：

1111111111111111111111111111111

1111111111111111111111111111111

-1>>>1竟然得到了int所能表示的最大整數，精彩。

除了使用-1>>>1能得到Integer.MAX_VALUE，以下的也能得到同樣的結果：

        //maxInt

        System.out.println(~(1 << 31));

        System.out.println((1 << -1)-1);

        System.out.println(~(1 << -1));

使用位運算往往能很巧妙的實現某些演算法完成一些複雜的功能。

常見使用

1.      m*2^n

可以使用m<<n求得結果，如：

        System.out.println("2^3=" + (1<<3));//2^3=8

        System.out.println("3*2^3=" + (3<<3));//3*2^3=24

計算結果是不是很正確呢？如果非要說2<<-1為什麼不等於0.5，前面說過，位運算的運算元只能是整型和字元型。在求int所能表示的最小值時，可以使用

//minInt

System.out.println(1 << 31);

System.out.println(1 << -1);

可以發現左移31位和-1位所得的結果是一樣的，同理，左移30位和左移-2所得的結果也是一樣的。移動一個負數位，是不是等同於右移該負數的絕對值位呢？輸出一下就能發現不是的。java中int所能表示的最大數值是31位，加上符號位共32位。在這裡可以有這樣的位移法則：

法則一：任何數左移（右移）32的倍數位等於該數本身。

法則二：在位移運算m<<n的計算中，若n為正數，則實際移動的位數為n%32，若n為負數，則實際移動的位數為(32+n%32)，右移，同理。

左移是乘以2的冪，對應著右移則是除以2的冪。

2.      判斷一個數n的奇偶性

n&1 == 1?”奇數”:”偶數”

為什麼與1能判斷奇偶？所謂的二進位制就是滿2進1，那麼好了，偶數的最低位肯定是0（恰好滿2，對不對？），同理，奇數的最低位肯定是1.int型別的1，前31位都是0，無論是1&0還是0&0結果都是0，那麼有區別的就是1的最低位上的1了，若n的二進位制最低位是1（奇數）與上1，結果為1，反則結果為0.

3.      不用臨時變數交換兩個數

在int[]陣列首尾互換中，是不看到過這樣的程式碼：

    public static int[] reverse(int[] nums){
        int i = 0;
        int j = nums.length-1;
        while(j>i){
            nums[i]= nums[i]^nums[j];
            nums[j] = nums[j]^nums[i];
            nums[i] = nums[i]^nums[j];
            j--;
            i++;
        }
        return nums;
    }

上面的計算主要遵循了一個計算公式：b^(a^b)=a。

我們可以對以上公式做如下的推導：

任何數異或本身結果為0.且有定理a^b=b^a。異或是一個無順序的運算子，則b^a^b=b^b^a，結果為0^a。

再次列出異或的計算表:

可以發現，異或0具有保持的特點，而異或1具有翻轉的特點。使用這些特點可以進行取數的操作。

         那麼0^a，使用異或0具有保持的特點，最終結果就是a。

其實java中的異或運演算法則完全遵守數學中的計演算法則：

①    a ^ a =0

②    a ^ b =b ^ a

③    a ^b ^ c = a ^ (b ^ c) = (a ^ b) ^ c;

④    d = a ^b ^ c 可以推出 a = d ^ b ^ c.

⑤    a ^ b ^a = b.

4.      取絕對值

(a^(a>>31))-(a>>31)

先整理一下使用位運算取絕對值的思路：若a為正數，則不變，需要用異或0保持的特點；若a為負數，則其補碼為原始碼翻轉每一位後+1，先求其原始碼，補碼-1後再翻轉每一位，此時需要使用異或1具有翻轉的特點。

任何正數右移31後只剩符號位0，最終結果為0，任何負數右移31後也只剩符號位1，溢位的31位截斷，空出的31位補符號位1，最終結果為-1.右移31操作可以取得任何整數的符號位。

那麼綜合上面的步驟，可得到公式。a>>31取得a的符號，若a為正數，a>>31等於0，a^0=a，不變；若a為負數,a>>31等於-1 ，a^-1翻轉每一位.

小結

在日常的java開發中位運算使用的不是很常見，但是面試或考試中會有涉及的地方，雖然不是決定項，但卻是加分項，說明對計算機語言有最起碼的瞭解。而且在高階演算法中，位運算往往能優化演算法執行效率，減少執行時間。再比如，有一張全是選擇題或是勾選題（類似判斷）的試卷，你是使用每個選項一條記錄的形式儲存答案還是使用一個二進位制對應的整數來儲存答案？就像是英語考試中的答題卡：

每個題目有4個選項，每個選項有兩個狀態：選、不選（1、0），那麼此時是不是可以使用4位二進位制數來表示某題的答案呢？