[CTF]維吉尼亞密碼(維基利亞密碼)
[CTF]維吉尼亞密碼(維基利亞密碼)
----------------------百度百科
https://baike.baidu.com/item/維吉尼亞密碼/4905472?fr=aladdin
維吉尼亞密碼(又譯維熱納爾密碼)是使用一系列凱撒密碼組成密碼字母表的加密演算法,屬於多表密碼的一種簡單形式。
| 中文名 | 維吉尼亞密碼 |
| 外文名 | Vigenère cipher |
| 出 處 | 吉奧萬巴蒂斯塔貝拉索先生的密碼 |
| 性 質 | 加密演算法 |
| 名詞解釋 | 愷撒密碼的基礎上擴充套件的多表密碼 |
| 組成元素 | 明文、金鑰、密表 |
描述
在一個凱撒密碼中,字母表中的每一字母都會作一定的偏移,例如偏移量為3時,A就轉換為了D、B轉換為了E……而維吉尼亞密碼則是由一些偏移量不同的愷撒密碼組成。
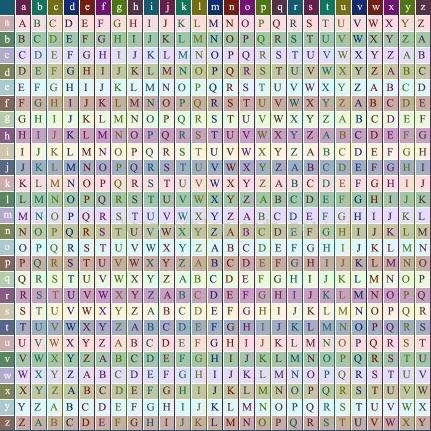
為了生成密碼,需要使用表格法。這一表格(如圖1所示)包括了26行字母表,每一行都由前一行向左偏移一位得到。具體使用哪一行字母表進行編譯是基於金鑰進行的,在過程中會不斷地變換。

圖1.表格
例如,假設明文為:
ATTACKATDAWN
選擇某一關鍵詞並重復而得到金鑰,如關鍵詞為LEMON時,金鑰為:
LEMONLEMONLE
對於明文的第一個字母A,對應金鑰的第一個字母L,於是使用表格中L行字母表進行加密,得到密文第一個字母L。類似地,明文第二個字母為T,在表格中使用對應的E行進行加密,得到密文第二個字母X。以此類推,可以得到:
明文:ATTACKATDAWN金鑰:LEMONLEMONLE密文:LXFOPVEFRNHR
解密的過程則與加密相反。例如:根據金鑰第一個字母L所對應的L行字母表,發現密文第一個字母L位於A列,因而明文第一個字母為A。金鑰第二個字母E對應E行字母表,而密文第二個字母X位於此行T列,因而明文第二個字母為T。以此類推便可得到明文。
用數字0-25代替字母A-Z,維吉尼亞密碼的加密文法可以寫成同餘的形式:
![]()
解密方法則能寫成:
![]()
密碼破譯
對包括維吉尼亞密碼在內的所有多表密碼的破譯都是以字母頻率為基礎的,但直接的頻率分析卻並不適用。例如,如果P是密文中出現次數最多的字母,則P很有可能對應E(前提是明文的語言為英語)。原因在於E是英語中使用頻率最高的字母。然而,由於在維吉尼亞密碼中,E可以被加密成不同的密文,因而簡單的頻率分析在這裡並沒有用。
破譯維吉尼亞密碼的關鍵在於它的金鑰是迴圈重複的。如果我們知道了金鑰的長度,那密文就可以被看作是交織在一起的凱撒密碼,而其中每一個都可以單獨破解。使用卡西斯基試驗和弗裡德曼試驗來得到金鑰的長度。
卡西斯基試驗
弗里德里希·卡西斯基於1863年首先發表了完整的維吉尼亞密碼的破譯方法,稱為卡西斯基試驗(Kasiski examination)。早先的一些破譯都是基於對於明文的認識、或者使用可識別的詞語作為金鑰。而卡西斯基的方法則沒有這些限制。然而,在此之前,已經有人意識到了這一方法。1854年,查爾斯·巴貝奇受到斯維提斯(John Hall Brock Thwaites)在《藝術協會雜誌》(Journal of the Society of the Arts)上聲稱發明了“新密碼”的激勵,從而破譯了維吉尼亞密碼。巴貝奇發現斯維提斯的密碼只不過是維吉尼亞密碼的一個變種而已,而斯維提斯則向其挑戰,讓他嘗試破譯用兩個不同長度的金鑰加密的密文。巴貝奇成功地進行了破譯,得到的明文是丁尼生所寫的詩《罪惡的想象》(The Vision of Sin),使用的金鑰則是丁尼生妻子的名字Emily(艾米莉)。巴貝奇從未對他的方法進行過解釋 。在對巴貝奇生前筆記的研究中發現,早在1846年巴貝奇就使用了這一方法,與後來卡西斯基發表的方法相同。
卡西斯基試驗是基於類似the這樣的常用單詞有可能被同樣的金鑰字母進行加密,從而在密文中重複出現。例如,明文中不同的CRYPTO可能被金鑰ABCDEF加密成不同的密文:
金鑰:ABCDEF AB CDEFA BCD EFABCDEFABCD
明文:CRYPTO IS SHORT FOR CRYPTOGRAPHY
密文:CSASXT IT UKSWT GQU GWYQVRKWAQJB
此時明文中重複的元素在密文中並不重複。然而,如果金鑰相同的話,結果可能便為(使用金鑰ABCD):
金鑰:ABCDAB CD ABCDA BCD ABCDABCDABCD
明文:CRYPTO IS SHORT FOR CRYPTOGRAPHY
密文:CSASTP KV SIQUT GQU CSASTPIUAQJB
此時卡西斯基試驗就能產生效果。對於更長的段落此方法更為有效,因為通常密文中重複的片段會更多。如通過下面的密文就能破譯出金鑰的長度:
密文:DYDUXRMHTVDVNQDQNWDYDUXRMHARTJGWNQD
其中,兩個DYDUXRMH的出現相隔了18個字母。因此,可以假定金鑰的長度是18的約數,即長度為18、9、6、3或2。而兩個NQD則相距20個字母,意味著金鑰長度應為20、10、5、4或2。取兩者的交集,則可以基本確定金鑰長度為2。
弗裡德曼試驗
弗裡德曼試驗由威廉·F·弗裡德曼(William F. Friedman)於1920年代發明。他使用了重合指數(index of coincidence)來描述密文字母頻率的不勻性,從而破譯密碼。
![]()
指目標語言中兩個任意字母相同的概率(英文中為0.067),
![]()
指字母表中這種情況出現的概率(英文中為1/26=0.0385),從而金鑰長度可以估計為:
![]()
其中,觀察概率為
![]()
其中,c是指字母表的長度(英文為26),N指文字的長度,n1到nc是指密文的字母頻率,為整數。
此方法只是一種估計,會隨著文字長度的增加而更為精確。在實踐中,會嘗試接近此估計的多個金鑰長度。一種更好的方法是將密文寫成矩陣形式,其中列數與假定的金鑰長度一致,將每一列的重合指數單獨計算,並求得平均重合指數。對於所有可能的金鑰長度,平均重合指數最高的最有可能是真正的金鑰長度。這樣的試驗可以作為卡西斯基試驗的補充。 [3]
頻率分析
一旦能夠確定金鑰的長度,密文就能重新寫成多列,列數與金鑰長度對應。這樣每一列其實就是一個凱撒密碼,而此密碼的金鑰(偏移量)則對應於維吉尼亞密碼金鑰的相應字母。與破譯凱撒密碼類似的方法,就能將密文破譯。
柯克霍夫方法作為卡西斯基試驗的改進,由奧古斯特·柯克霍夫(Auguste Kerckhoffs)提出。它將每一列的字母頻率與轉換後的明文頻率相對應而得出每一列的金鑰字母。一旦金鑰中每一個字母都能確定,就能很簡單地破譯密文,從而得到明文。如果維吉尼亞字母表表格本身是雜亂而非按通常字母表順序的話,那柯克霍夫方法就會無效,但卡西斯基試驗和重複指數對於決定金鑰長度仍舊是有效的。
變體
維吉尼亞密碼的變體滾動金鑰密碼也曾一度被認為是不可破譯的。這種變體的金鑰與密文的長度一致,因此卡西斯基試驗和弗裡德曼試驗即變得無效。1920年,弗裡德曼首先發現了此方法的弱點。由於滾動金鑰密碼的金鑰是一段真實的語言,因而破譯者便能瞭解金鑰文字的統計資訊,而這種資訊也會反映到密文當中。
如果金鑰是完全隨機、與明文的長度一致且只使用過一次,維吉尼亞密碼理論上是不可破譯的。然而,這種情況下金鑰本身而非密文便成了關鍵,這被稱為一次性密碼本。
維吉尼亞本人確實發明了一種更強的維吉尼亞密碼變體——自動金鑰密碼。巴貝奇所破譯的其實是這種自動金鑰密碼,而卡西斯基則通常被認為是首先發表了破譯固定金鑰多表密碼的方法。
還有一種簡單的變體使用維吉尼亞的解碼方法進行加密,同時使用維吉尼亞的加密方法進行解密,這被稱為變異博福特密碼。此方法與弗朗西斯·博福特創造的博福特密碼不同,後者雖然也與維吉尼亞密碼相似,但使用了修改過的加密方式和表格,是一種對等加密。
維吉尼亞密碼錶面上的強度並沒能使其在歐洲得到廣泛使用。由Gronsfeld伯爵所創造的Gronsfeld密碼基本與維吉尼亞密碼相同,不過它只使用10個不同的密碼字母表(對應字母0到9)。Gronsfeld密碼的強度很高,這是因為它的金鑰並不是一個單詞,但缺點在於字母表數量過少。儘管如此,Gronsfeld密碼仍在德國和整個歐洲有著廣泛的應用。