演算法 | 生命遊戲 (Game of Life)
演算法 | 生命遊戲
概要: 本文將要介紹一個名為“生命遊戲”的有趣演算法並用C++進行簡單的實現。 關鍵字: C++;生命遊戲演算法1 背景說明
生命遊戲,又叫康威生命遊戲(Conway’s Game of Life),或康威生命棋,是英國數學家約翰·康威(John Conway)在1970年發明的細胞自動機。它最初在1970年10月在《科學美國人》雜誌上的“數學遊戲”專欄出現。我大一暑假在上暑期課程時無意中接觸到這個概念,並被它看似簡單的外表、實則複雜的“內心”所吸引,於是出於好奇就自己用C++模擬了一翻,直到最近整理本科成果時又一次翻到了這個小巧有趣的程式碼。程式碼很短,只有一二百行,其中核心的判斷和計算的部分只有十來行;其演算法更是簡單,幾句話就可以描述清楚。下面我將做簡要的介紹。
2 演算法原理
2.1 概述
生命遊戲是一個零玩家遊戲。它發生在一個二維矩形世界,這個世界的基本組成單位是一個一個等大的小方格。每個方格居住著一個活著的或死了的細胞。一個細胞在下一個時刻生死取決於相鄰八個方格中活著的細胞的數量。一方面,如果相鄰方格活著的細胞數量過多,這個細胞會因為資源匱乏而在下一個時刻死去;另一方面,如果周圍活細胞過少,這個細胞會因太孤單而死去。而只有其周圍的細胞數量適合時,這個方格中的細胞才能繼續存活。若方格中原來的細胞已經死亡,在其周圍細胞數量合適時,也會使得該死細胞“死而復生”,這可以認為是在模擬細胞的繁殖。玩家可以設定周圍活細胞的數目怎樣時才事宜細胞生存和繁殖。但是需要注意的是,如果這個數目設定過高,世界中的大部分細胞會因為找不到太多的活的鄰居而死去,直到整個世界都沒有生命;如果這個數目設定過低,世界中又會被生命充滿而沒有什麼變化。
實際遊戲中,這個數目一般選取2或者3;這樣整個生命世界才不至於太過荒涼或擁擠,而是出於一種動態平衡之中。如此一來,遊戲的規則就是:當一個方格周圍有2或3個活細胞時,方格中的活細胞在下一個時刻繼續存活;即使這個時刻方格中沒有活細胞,在下一個時刻也會“誕生”活細胞。否則,這個方格中的細胞會死亡,或不誕生新的活細胞。
2.2 規則
在選取了合適的資料後,對具體規則作如下描述。
生命遊戲中,對於任意細胞: 每個細胞有兩種狀態:存活或死亡。每個細胞與以自身為中心的周圍八格細胞產生互動。 1.當前細胞為存活狀態時,當週圍的活細胞低於2個時, 該細胞因孤獨而死亡; 2.當前細胞為存活狀態時,當週圍有2個或3個活細胞時, 該細胞保持原樣;
3 程式實現
我用C++模擬了上述過程。此演算法的核心在於計算下一代細胞的存亡圖景,程式碼如下所示:
void NextG(int p[][MAXLIS],int q[][MAXLIS])
{
int i,j,x,y;
int judge;
for(i = 0;i < MAXROW;i++)
{
for(j = 0;j < MAXLIS;j++)
{
if(p[i][j] == ALIVE)
{
judge = -1; //每一輪結束judge都要復位
}
else if(p[i][j] == DEAD)
{
judge = 0;
}
for(x = MAX(i-1,0);x<=MIN(i+1,MAXROW-1);x++) //開始這裡的MAXROW和MAXLIS後面忘記-1,邏輯出錯找了好久
{
for(y = MAX(j-1,0);y<=MIN(j+1,MAXLIS-1);y++)
{
if(p[x][y] == ALIVE)
judge +=1;
}
}
switch(judge)
{
case 2:q[i][j] = p[i][j];break; // 周圍有2個活細胞,保持原樣
case 3:q[i][j] = ALIVE;break; // 周圍有3個活細胞,生則繼續,死則復活(模擬繁殖)
default:q[i][j] = DEAD;break; // 周圍有1或4-8個活細胞,死(模擬擁擠而死或孤獨而死)
}
}
}
}
程式碼本身可以說是相當簡單了,學過陣列的人都能寫出來。剩下的就是一些裝飾門面的活兒,比如說我當時寫的測試程式碼——即main()函式——是長這個樣子的:
int main()
{
int CHOICE = 1,n = 0;
int choice;
int map[MAXROW][MAXLIS] = {DEAD},newmap[MAXROW][MAXLIS] = {DEAD}; //定義2個同維陣列並初始化為全0陣列
cout<<"_________________________________________"<<endl;
cout<<"| |"<<endl;
cout<<"| 歡迎來到“生命遊戲”! |"<<endl;
cout<<"| |"<<endl;
cout<<"| 請選擇初始化模式: |"<<endl;
cout<<"| |"<<endl;
cout<<"| 1.自動模式A 2.自動模式B |"<<endl;
cout<<"| |"<<endl;
cout<<"| 3.隨機模式 4.手動模式 |"<<endl;
cout<<"|________________________________________|"<<endl;
cin>>choice;
switch(choice)
{
case 1:Init1(map);break; //二維陣列作為函式引數被呼叫時,引數是二維陣列的起始位指標,也就是陣列名
case 2:Init2(map);break;
case 3:Init3(map);break;
case 4:Init4(map);break;
default:
{
cout<<"預設為隨機初始化模式."<<endl;
Init3(map);
break;
}
}
cout<<endl<<"父代細胞生存圖:"<<endl;
ShowMap(map);
while(CHOICE)
{
NextG(map,newmap);
CopyClc(map,newmap);
cout<<endl<<"子"<<n++<<"代細胞生存圖:"<<endl;
ShowMap(map);
cout<<"\n繼續請按除0以外的任意數字鍵."<<endl;
cin>>CHOICE;
}
cout<<"您已退出遊戲."<<endl;
return 0;
}
這裡我給出了4種初始化的條件供使用者選擇,同時為了讓使用者看清中間的每一個步驟,我讓使用者自己步進操作,也省了設定步進時長的麻煩,當然這些都是小細節。另外,很多人直接把這個例程寫在了網頁上,大家也可以去感受一下,推薦的網址有連結1和連結2。
4 結果分析
程式碼跑通之後就可以隨意玩耍了!執行的介面如圖1所示:
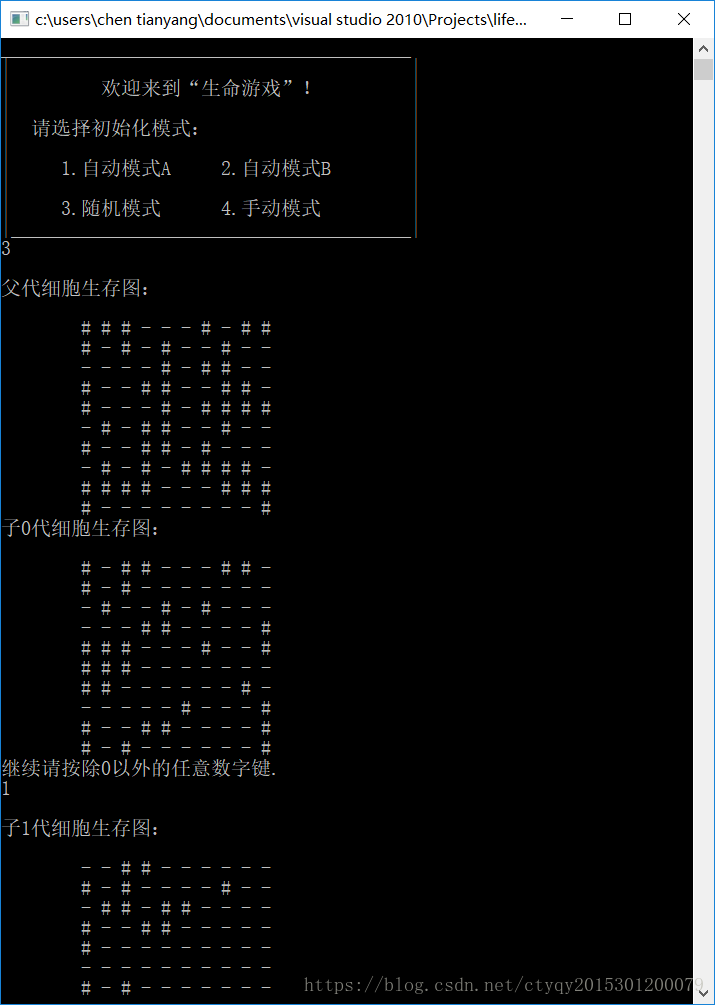
上圖中,“#”表示活細胞,“-”表示死細胞。
在測試的過程中,可以發現這樣一些如下所介紹的穩定結果。
4.1 情形一
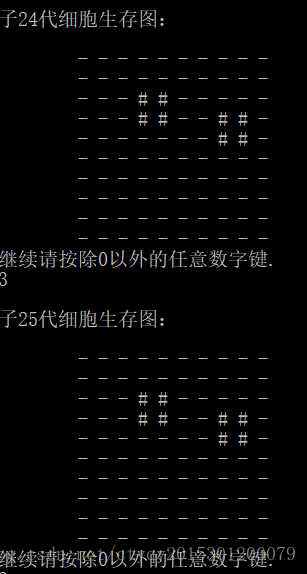
當父代如圖2所示時,子代執行到第24代即可保持穩定,如圖3所示。

4.2 情形二
當父代如圖4所示時,子代執行到第5代即可保持穩定,如圖5所示。


值得注意的是,雖然子5代和子6代細胞的生存圖不一致,但是以後所有子代的生存圖都是子5代和子6代的迴圈,因此這也是穩定的。
4.3 情形三
當細胞數量稍多一些,父代如圖6所示時,子代執行到第9代即可保持穩定,如圖7所示。

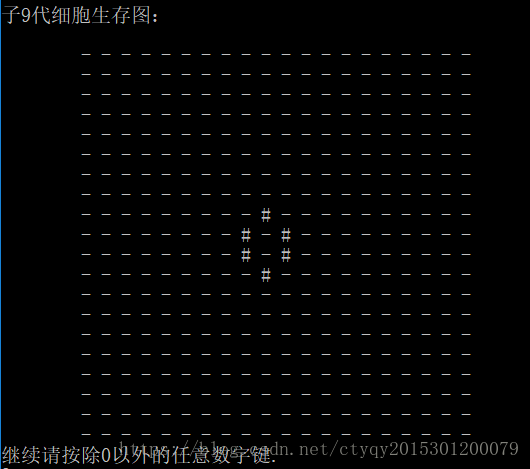
類似於情形一的“田”字型,這裡的6個活細胞構成的空間結構也是穩定的。
4.4 情形四
最後再嘗試一次,父代如圖8所示時,子代執行到第77代即可保持穩定,如圖9所示。
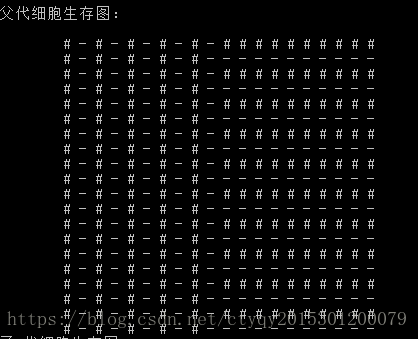
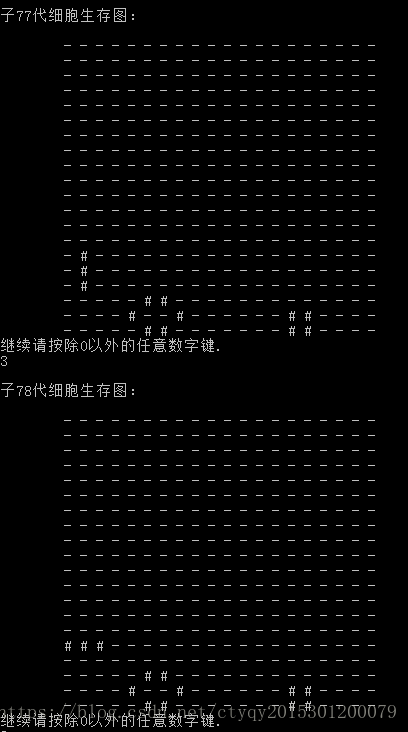
情形四恰好包含了情形一到情形三的內容,當然也是穩定的。
5 後記
“生命遊戲”雖然是一個零玩家遊戲,但卻經久不衰。它一直吸引著大量的愛好者的視線,其中包含的樂趣當然不止我所描述的這些。只要上網一查就能找到許多有趣的討論,比如知乎對生命遊戲穩定圖形的探討、果殼網對於計算和宇宙的關係的專訪報告以及嗶哩嗶哩和YouTube上的一些有趣視訊等,如果你有興趣,此話題大有繼續探討的空間和價值。
程式碼已上傳至網路,點選連結下載,密碼是9hrg。
