題意：給出n條邊，問：如果有相交，輸出burned！，沒有輸出ok！，注意下，這題還說了，相交於端點是不算交叉的。

　我們分兩步確定兩條線段是否相交：

　(1)快速排斥試驗

　　　設以線段 P1P2 為對角線的矩形為R， 設以線段 Q1Q2 為對角線的矩形為T，如果R和T不相交，顯然兩線段不會相交。

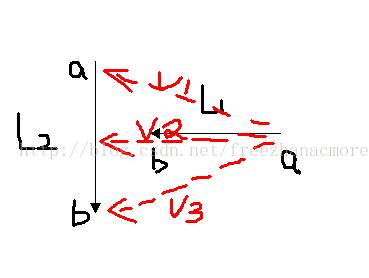
　(2)跨立試驗 　　　　如果兩線段相交，則兩線段必然相互跨立對方。若P1P2跨立Q1Q2 ，則向量 ( P1 - Q1 ) 和( P2 - Q1 )位於向量( Q2 - Q1 ) 的兩側，即( P1 - Q1 ) × ( Q2 - Q1 ) * ( P2 - Q1 ) × ( Q2 - Q1 ) < 0。上式可改寫成( P1 - Q1 ) × ( Q2 - Q1 ) * ( Q2 - Q1 ) × ( P2 - Q1 ) > 0。當 ( P1 - Q1 ) × ( Q2 - Q1 )

在相同的原理下，對此演算法的具體的實現細節可能會與此有所不同，除了這種過程外，大家也可以參考《演算法導論》上的實現。

　有了上面的基礎，這個演算法就很容易了。如果線段P1P2和直線Q1Q2相交，則P1P2跨立Q1Q2，即：( P1 - Q1 ) × ( Q2 - Q1 ) * ( Q2 - Q1 ) × ( P2 - Q1 ) >= 0。（這裡等於0，表示的是相交於端點，注意看清題意）

注意：一般情況下，為了避免跨立不相交的局面，一定要判斷線段P1P2跨立Q1Q2後再反過來判斷Q1Q2跨立P1P2如果兩者都跨立，才能斷定他們相交

///P1P2 橫跨 Q1Q2：

/// ( P1 - Q1 )×( Q2 - Q1 )*( Q2 - Q1 )×( P2 - Q1 ) > =0

#include<bits/stdc++.h>
using namespace std;

const int maxn=2010;

struct Point
{
    double x,y;

    Point() {}

    Point(double _x,double _y){
        x=_x;y=_y;
    }

    Point operator -(const Point &b) const{
        return Point(x-b.x,y-b.y);
    }
};

struct Line
{
    Point a,b;

    Line() {}

    Line(Point _a,Point _b){
        a=Point(_a.x,_a.y);
        b=Point(_b.x,_b.y);
    }
}line[maxn];

double Cross(Point a,Point b) ///叉積
{
//    printf("a.x=%f,a.y=%f,b.x=%f,b.y=%f\n",a.x,a.y,b.x,b.y);
    return a.x*b.y-a.y*b.x;
}

const double esp=1e-5;

int dcmp(double x)
{
    if(fabs(x)<esp) return 0;
    else return x>0?1:-1;
}
bool isCross(Line L1,Line L2) ///判斷跨立相交
{
    ///L2橫跨L1
    double tmp1=Cross(L2.a-L1.a,L1.b-L1.a);
    double tmp2=Cross(L1.b-L1.a,L2.b-L1.a);

    ///L1橫跨L2
    double tmp3=Cross(L1.a-L2.a,L2.b-L2.a);
    double tmp4=Cross(L2.b-L2.a,L1.b-L2.a);

//    printf("%f %f %f %f\n",tmp1,tmp2,tmp3,tmp4);
    if(dcmp(tmp1*tmp2)>0 && dcmp(tmp3*tmp4)>0) return true;
    ///都大於0，就說明兩線段相交，這裡就不等於0了，因為題目已經要求了不算入端點相交
    return false;
}
int main()
{

    int n;
    while(~scanf("%d",&n))
    {
        Point a,b;
        for(int i=0;i<n;i++)
        {
            scanf("%lf%lf%lf%lf",&a.x,&a.y,&b.x,&b.y);
            line[i]=Line(a,b);
        }

        int flag=1;

        for(int i=1;i<n;i++) ///這裡為什麼不用雙重迴圈？因為第3條邊和第1條邊只需比較一次就行了
        {
            for(int j=0;j<i;j++)
            {
                if(isCross(line[i],line[j])){
                    flag=0;break;
                }
            }
        }

        if(flag) printf("ok!\n");
        else printf("burned!\n");
    }

    return 0;
}