希爾排序也是一種插入排序演算法，也叫作縮小增量排序，是直接插入排序的一種更高效的改進演算法。

希爾排序因其設計者希爾（Donald Shell）的名字而得名，該演算法在 1959 年被公佈。一些老版本的教科書和參考手冊把該演算法命名為 Shell-Metzner，包含了 Marlene Metzner Norton 的名字，但是 Metzner 說：“我沒有為這種演算法做任何事，我的名字不應該出現在這個演算法的名字中。”

希爾排序在插入排序的基礎上，主要通過兩點來改進排序演算法：

1. 插入排序在對近似有序的數列進行排序時，排序效能會比較好；
2. 插入排序的效能比較低效，即每次只能將資料移動一位。

希爾排序的原理

希爾排序的基本思想是：把待排序的數列按照一定的增量分割成多個子數列。但是這個子數列不是連續的，而是通過前面提到的增量，按照一定相隔的增量進行分割的，然後對各個子數列進行插入排序，接著增量逐漸減小，然後仍然對每部分進行插入排序，在減小到1之後直接使用插入排序處理數列。

需要特別強調，這裡選擇增量的要求是每次都要減少，直至最後一次變為1為止。

下面，我們通過一個例項來理解其實現原理。

在本例項中的首選增量為 n/2，n 為待排序的數列的長度，並且每次的增量都為上一次的 1/2。待排序的數列為 588、392、898、115、306、62、909、902、789、234，有 10 個數。我們首選增量為 10/2 即 5，進行如圖 1 所示的分塊。

由於增量為 5，所以把原待排序的數列按照增量劃分為 5 組，每組實際上都是以增量為間隔的（陣列下標為0的元素對應下標為 5 的元素，1 對應 6、2 對應 7，等等）。

之後對每組進行插入排序，其實就是將後一個元素與前一個元素進行比較，看看是否需要交換（當然，還是應該按照插入排序的步驟來進行，就是把後一個元素拿出來，與前一個元素進行比較，看看是否需要移動前面的元素，如果需要移動，則把第 1 個元素後移，然後把拿出來的元素放到前面去；若不需要移動，則不需要進行其他操作）。

分別對每組元素進行插入排序之後的結果如圖 2 所示。

我們發現，實際上在這組數列中只有兩組資料進行了移動操作。至此，第 1 趟排序完成。現在的待排序的數列變成了 62、392、898、115、234、588、909、902、789、306。接下來我們該縮減增量了，按照之前的規則，這次的增量應該是 5/2，也就是 2，於是出現瞭如圖 3 所示的劃分結果。

現在的待排序的數列的增量為 2，所以每隔一個元素進行分組（也就是陣列下標為 0、2、4、6、8 的元素為一組，陣列下標為 1、3、5、7、9 的元素為一組），當前的數列被劃分為兩組，繼續對每組數列進行插入排序。

這裡就不再複述插入排序的步驟了，大家應該可以輕易地完成對兩組資料的插入排序了。第 2 趟排序的結果如圖 4 所示。現在的待排序的數列變為 62、115、234、306、789、392、898、588、909、902。

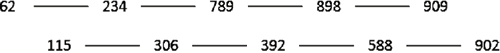
我們發現，每趟排序都會使陣列整體更趨於有序了。

接下來對增量繼續按照規則除以 2，得到 1，說明這時該對上一趟完成排序的數列進行直接插入排序了。第3趟排序的結果就是最終結果：62、115、234、306、392、588、789、898、902、909，至此希爾排序結束。是不是覺得希爾排序很簡單？

希爾排序的實現

希爾排序實際上只是對插入排序的一種改進，在演算法的實現上，我們需要額外操作的只有對增量的處理及對數列的分塊處理。

下面我們一起來看看希爾排序的程式碼實現：

public class ShellSort {
    public static void main(String[] args) {
        int[] array = {5, 9, 1, 9, 5, 3, 7, 6, 1}; // 待排序陣列
        sort(array);
        print(array);
    }

    public static void sort(int array[]) {
        int temp;
        for (int k = array.length / 2; k > 0; k /= 2) {
            for (int i = k; i < array.length; i++) {
                for (int j = i; j >= k; j -= k) {
                    if (array[j - k] > array[j]) {
                        temp = array[j - k];
                        array[j - k] = array[j];
                        array[j] = temp;
                    }
                }
            }
        }
    }

    /**
     * 列印陣列
     */
    public static void print(int array[]) {
        for (int i = 0; i < array.length; i++) {
            System.out.print(array[i] + "   ");
        }
        System.out.println();
    }
}

希爾排序的特點及效能

其實希爾排序只使用了一種增量的方式去改進插入排序，從上述對該演算法的描述及例項中，我們能夠清楚地知道實際上希爾排序在內部還是使用插入排序進行處理的。但是這個增量確實有它的意義，不管數列有多長，剛開始時增量會很大，所以每一組待排序的數列的規模會很小，排序會很快。儘管後來數列的規模慢慢變大，但是數列整體已經開始趨於有序了，所以插入排序的速度還是越來越快的。

在時間複雜度上，由於增量的序列不一定，所以時間複雜度也不確定。這在數學上還無法給出確切的結果。我們在上面採用的是每次除以 2 的方式，但是據研究，有以下幾種可推薦的序列：

• N/3+1，N/3²+1，N/3³+1……（據說在序列數 N<100 000 時最優）；
• 2^k-1，2^(k-1)-1，2^(k-2)-1……（設 k 為總趟數）；
• 其他的還有質數法等。

對於每次除以 2 的增量選擇，希爾排序的最好情況當然是本身有序，每次分割槽都不用排序，時間複雜度是 O(n)；但是在最壞的情況下仍然每次都需要移動，時間複雜度與直接插入排序在最壞情況下的時間複雜度沒什麼區別，也是 O(n²)。

但是一般認為希爾排序的平均時間複雜度是 O(n^1.3)。當然，希爾排序的時間複雜度與其增量序列有關，我們知道，一般來說希爾排序會比插入排序快一些，這就足夠了。

在希爾排序的實現中仍然使用了插入排序，只是進行了分組，並沒有使用其他空間，所以希爾排序的空間複雜度同樣是 O(1)，是常量級的。

在希爾排序中會進行分組、排序，所以同樣值的元素，其相對位置有可能會發生變化，這是因為同樣值的元素若不在一個組中，則有可能後面的元素會被移動到前面。所以希爾排序是不穩定的演算法。

希爾排序的適用場景

在使用希爾排序時，需要選擇合適的增量序列作為排序輔助，而這也是一個比較複雜的抉擇。所以希爾排序在實際使用排序時並不常用。

但是作為一個優化排序的思想，我們還是應該好好學習它。