如果學不會也不要打我。 假設你會線段樹 開始！ --- 主席樹也叫可持久化線段樹

顧名思義，它能夠儲存線段樹在每個時刻的版本。

什麼叫每個時刻的版本？你可能對一棵普通線段樹進行各種修改，這每種樣子就是我們所說的不同時刻的版本。

假設我們對線段樹進行單點修改，維護區間和。 每次修改操作中，只有logn個節點會被修改，我們可以複製這些被修改的節點，而不復制沒有被改變的節點（以提高效率）。 最後通過特殊的方式建立出新時刻的樹。

建造方式如下：

假設上一時刻的樹長這樣：

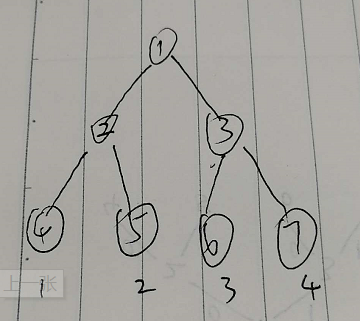
現在進行修改操作，對下標為3的位置修改，也就是說修改1 3 6號節點。若是普通線段樹，則直接修改1 3 6三個節點。但是在主席樹中，我們不直接在1 3 6號節點上修改。而是新建3個節點，分別對應1 3 6號節點，對新建節點進行本想在1 3 6號節點進行的操作（“本想”指普通線段樹）。 如圖：

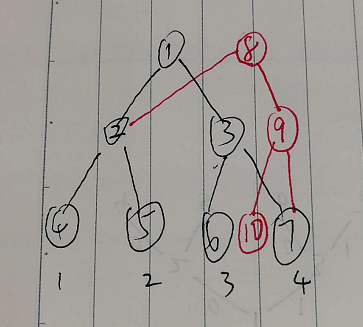
關於不同版本的線段樹理解

接上圖，可以觀察到，1號和8號往下分別是兩棵不同版本的線段樹，不同版本共用很多節點。這並不會影響自上而下的查詢。

單點修改的例子

以下內容質量不高：

寒羽吾: 用主席樹做kth number，就是在空線段樹的基礎上，依次線上段樹的位置a[1]處加一，a[2]處加一。即用線段樹維護值在某區間中的ai有多少個。然後可以線上段樹上移動指標，找到第k個。

寒羽吾: 考慮區間[l,r]的限制，即r時刻的線段樹減去l-1時刻的線段樹，就得到維護ai（下標i在[l,r]中）的線段樹了。

寒羽吾: 查詢的時候不必真把做差得到的線段樹求出來，需要這個線段樹的什麼位置就訪問r版本和l-1版本的對應點，取出值相減即可。

寒羽吾: 上面是我寫的板子，t表示樹節點，w[0]左孩子w[1]右孩子。

寒羽吾: 理論上維護21e9個元素的線段樹是開不下節點的（也是時間上不可建立的），但因為主席樹的特殊性：只建立需要用（改變）的節點。所以可以不對ai進行離散化，直接建立“看似”能維護21e9個元素的線段樹。

#include<bits/stdc++.h>
using namespace std;
struct node{
    int sum;
    int w[2];
}t[5000005];
int np;
int n,m;
int st[100005];
int a[100005];
void plu(int x,int c,int num){
    int now=++np;
    t[now]=t[x];
    if(c<0){
        t[now].sum++;
        return;
    }
    int p=(num>>c)&1;
    plu(t[now].w[p],c-1,num);
    t[now].w[p]=now+1;
    t[now].sum=t[t[now].w[0]].sum+t[t[now].w[1]].sum;
}
int solve(int l,int r,int k){
    int lx=st[l-1],rx=st[r],ans=0;
    for(int i=0;i<=30;i++){
        int p=0;
        if(t[t[rx].w[0]].sum-t[t[lx].w[0]].sum<k)
            k-=t[t[rx].w[0]].sum-t[t[lx].w[0]].sum,
            p=1;
        lx=t[lx].w[p],
        rx=t[rx].w[p],
        ans=ans<<1|p;
    }
    return ans;
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);
        a[i]+=1e9;
    }
    np=1;st[0]=1;
    for(int i=1;i<=n;i++){
        st[i]=np+1;
        plu(st[i-1],30,a[i]);
    }
    for(int i=1;i<=m;i++){
        int l,r,k;
        scanf("%d%d%d",&l,&r,&k);
        printf("%d\n",int(solve(l,r,k)-1e9));
    }
    return 0;
}