「資料結構與演算法 2」| 單鏈表其實真的很簡單。
寫在之前
在程式設計裡,我們經常需要將同為某個型別的一組資料元素作為一個整體來使用,需要建立這種元素組,用變數來記錄它們或者傳入函式等等等等,「線性表」就是這樣一組元素的抽象,它是某類元素的集合並且記錄著元素之間一種順序關係,是最基本的資料結構之一,在實際程式中運用非常廣泛,比如 Python 中的 list 和 tuple 都可以看作是線性表的實現。
基於各種實際操作等方面的綜合考慮,我們提出了兩種實現線性表的形式:「順序表」和「連結串列」。
「順序表」是將表中的元素順序存放在一大塊連續的儲存區間裡,所以在這裡元素間的順序是由它們的儲存順序來表示的。「連結串列」則是將表中元素存放在一系列的結點中(結點的儲存位置可以是連續的,可以是不連續的,也就意味著它們可以存在任何記憶體未被佔用的位置),這些結點通過連線構造起來,結點分為「資料域」和「指標域」。這次我們要學習的「單鏈表」就是「連結串列」的一種實現形式,「資料域」儲存著作為表元素的資料項,「指標域」儲存同一個表裡的下一個結點的標識。
在正式說「單鏈表」之前,我先來說一下很多人在學習連結串列之初都傻傻分不清的兩個東西:「頭結點」和「頭指標」。
「頭結點」的設立是為了操作的統一和方便,是放在第一個元素的節點之前,它的資料域一般沒有意義,並且它本身也不是連結串列必須要帶的。那設立頭節點的目的是什麼呢?其實就是為了在某些時候可以更方便的對連結串列進行操作,有了頭結點,我們在對第一個元素前插入或者刪除結點的時候,它的操作與其它結點的操作就統一了。
「頭指標」顧名思義,是指向連結串列第一個結點的指標,如果有頭結點的話,那麼就是指向頭結點的指標。它是連結串列的必備元素且無論連結串列是否為空,頭指標都不能為空,因為在訪問連結串列的時候你總得知道它在什麼位置,這樣才能通過它的指標域找到下一個結點的位置,也就是說知道了頭指標,整個連結串列的元素我們都是可以訪問的,所以它必須要存在,這也就是我們常說的「標識」,這也就是為什麼我們一般用頭指標來表示連結串列。
單鏈表
n 個結點連結成一個連結串列,這也就是平時書上所說的「鏈式儲存結構」,因為這個連結串列中的每個結點中只包含一個指標域,所以又叫「單鏈表」。單鏈表正是通過每個結點的指標域將線性表的資料元素按其邏輯次序連結在一起。單鏈表的第一個結點的儲存位置叫做「頭指標」,最後一個結點的指標為「空」,一般用 “^” 表示。
上圖是不帶頭結點的單鏈表,下面我們來看一下帶頭結點的單鏈表:
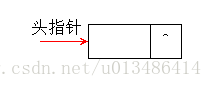
還有一種是空連結串列:
通過上面 3 個圖我們發現無論單鏈表是否為空,是否有頭結點,頭指標都是存在的,這就很好的印證了之前我們所說的「頭指標是連結串列的必備元素且無論連結串列是否為空,頭指標都不能為空」。
為了方便後續的操作,我們一般會先定義一個簡單的結點類:
class Node(object):
def __init__(self,data):
self.data = data
self.next = None
單鏈表的基本操作
首先我們先來建立一個連結串列類:
class LinkList(object):
def __init__(self):
self.head = Node(None)
# 判斷連結串列是否為空
def IsEmpty(self):
p = self.head # 頭指標
if p.next == None:
print("List is Empty")
return True
return False
# 列印連結串列
def PrintList(self):
if self.IsEmpty():
return False
p = self.head
while p:
print(p.data,end=' ')
p = p.next
1.建立單鏈表
建立單鏈表的過程其實就是一個動態生成連結串列的過程,說簡單點就是從一個「空連結串列」開始,依次建立各個元素的結點,並把它們逐個插入連結串列,時間複雜度為 O(n):
def InitList(self,data):
self.head = Node(data[0]) # 頭結點
p = self.head # 頭指標
for i in data[1:]:
node = Node(i)
p.next = node
p = p.next
下面我們來測試一下:
# test
lst = LinkList()
data = [1, 4, 5, 8, 2, 3]
lst.InitList(data)
lst.PrintList()
輸出結果如下:
1 4 5 8 2 3
2.計算單鏈表的長度
在使用連結串列的時候,經常需要求表的長度,為此我們可以建立一個球表長的函式,這個函式就是從左到右掃描,遍歷表中的所有結點並完成計數,時間複雜度為 O(n):
def LengthList(self):
if self.IsEmpty():
return 0
p = self.head
cnt = 0
while p:
cnt += 1
p = p.next
return cnt
下面我們來測試一下:
# test
lst = LinkList()
data = [1, 4, 5, 8, 2, 3]
lst.InitList(data)
print(lst.LengthList())
輸出的結果如下:
6
3.單鏈表的插入
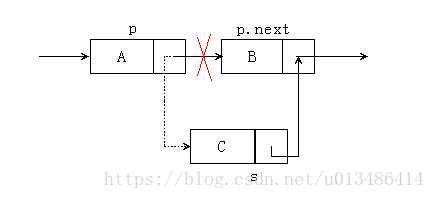
假設我們要將結點 s 插入到 結點 p 的後面,只需要將結點 s 插入到結點 p 和 結點 p.next 之間即可,說起來簡單,那麼到底如何插入呢?請看下圖:
由上圖我們可以看到,單鏈表結點的插入根本不需要驚動其它結點,只需要讓 s.next 和 p.next 的指標稍作改變即可。讓 p 的後繼結點改為 s 的後繼結點,再把 s 的後繼結點變成 p 的後繼結點。這裡一定要切記,插入操作的順序不能改變,至於為什麼,你可以拿起紙筆手動的畫一下,結果一下子就會出來(對於單鏈表的表頭和表尾的特殊情況,操作是相同的)。
# 單鏈表的插入(在第 s 個結點後面插入 data)
def InsertList(self,s,data):
if self.IsEmpty() or s < 0 or s > self.LengthList():
print("Insert failed!")
return
p = self.head
index = 1
while index < s:
p = p.next
index += 1
node = Node(data)
node.next = p.next
p.next = node
下面我們來測試一下:
# test
lst = LinkList()
data = [1, 4, 5, 8, 2, 3]
lst.InitList(data)
lst.InsertList(0,666)
lst.PrintList()
輸出的結果如下:
1 666 4 5 8 2 3
4.單鏈表刪除
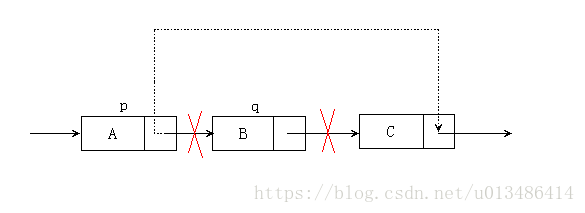
看完插入,我們現在再來看看單鏈表的刪除。假設我們想要刪除一個結點 q,其實就是將它的前繼結點 p 的指標繞過 q,直接指向 q 的後繼結點即可,具體操作如下圖所示:
由上圖可以看出,我們只需要一步就可以實現刪除操作,那就是讓 p.next 直接為 p 的 next 的 next,p 的 next 為 q,所以也就是 p.next = q.next,時間複雜度為 O(n)。
# 單鏈表的刪除(刪除第 s 個結點)
def DeleteList(self, s):
if self.IsEmpty() or s < 0 or s > self.LengthList():
print("Delete failed! ")
return
p = self.head
index = 1
while index < s:
pre = p
index += 1
p = p.next
pre.next = p.next
p = None
由 p = None 可以看出,在 Python 中,只需要簡單的將指標賦值為 None,就拋棄了連結串列原有的結點,Python 直譯器的儲存管理系統會自動回收不用的儲存。
下面我們來測試一下:
# test
lst = LinkList()
data = [1, 4, 5, 8, 2, 3]
lst.InitList(data)
lst.DeleteList(3)
lst.PrintList()
輸出的結果如下:
1 4 8 2 3
5.單鏈表的讀取
在順序結構中,我們想要獲取任意一個元素的儲存位置是很容易的,但是在單鏈表中,第 i 個元素到底在哪我們一開始沒辦法知道,只能傻傻的從頭開始找,所以在對於單鏈表獲取第 i 個元素的操作,演算法上相對麻煩一些。
# 單鏈表的讀取(獲取第 s 個結點的值)
def GetList(self, s):
if self.IsEmpty() or s < 0 or s > self.LengthList():
print("Read failed! ")
return
p = self.head
index = 1
while index < s:
index += 1
p = p.next
print("第 {} 個值為 {}".format(s, p.data))
從上面的程式碼我們可以很清楚的看出,單鏈表獲取第 i 個元素就是從頭開始找,知道第 i 個元素為止,所以我們可以很容易的估算出它的時間複雜度是 O(n)。任何事物都不是完美的,有好的地方就有壞的地方,元素的讀取就是單鏈表美中不足的地方之一。
寫在之後
單鏈表的操作其實還有不少,我只是寫了其中常用的幾種,希望大家能自己動手嘗試一下,把這幾個搞懂搞透。碰到這樣的問題從哪個方面去思考,如何去做才是最重要的,只有學會了這些,你在日後碰到相關問題的時候就知道如何去下手。
我在上面每個操作的講解中大多數給出了圖,通過圖來看解法題目瞭然。演算法這個東西其實就是這樣,多動手實現以下,想不明白了就動手畫一下,畫著畫著思路就出來了。
最後我們就來總結一下連結串列操作的時間複雜度,如果你還不會估算演算法的時間複雜度,請看我的 「 資料結構與演算法 1 」| 循序漸進理解時間複雜度和空間複雜度:
- 建立空表 O(1)。
- 建立單鏈表 O(n)
- 插入元素:首端插入為 O(1);尾端插入為 O(n),因為還要找到表的最後結點;定位插入 為O(n)。
- 刪除元素:首端刪除為 O(1);尾端刪除為 O(n),理由如上;定位刪除為 O(n)。
以下是上述所有操作的程式碼彙總:
# 結點類
class Node(object):
def __init__(self,data):
self.data = data
self.next = None
# 連結串列類
class LinkList(object):
def __init__(self):
self.head = Node(None)
# 判斷連結串列是否為空
def IsEmpty(self):
p = self.head # 頭指標
if p.next == None:
print("List is Empty")
return True
return False
# 列印連結串列
def PrintList(self):
if self.IsEmpty():
return False
p = self.head
while p:
print(p.data,end= ' ')
p = p.next
# 建立單鏈表
def InitList(self,data):
self.head = Node(data[0]) # 頭結點
p = self.head # 頭指標
for i in data[1:]:
node = Node(i)
p.next = node
p = p.next
# 單鏈表的長度
def LengthList(self):
if self.IsEmpty():
return 0
p = self.head
cnt = 0
while p:
cnt += 1
p = p.next
return cnt
# 單鏈表的插入(在第 s 個結點後面插入 data)
def InsertList(self,s,data):
if self.IsEmpty() or s < 0 or s > self.LengthList():
print("Insert failed!")
return
p = self.head
index = 1
while index < s:
p = p.next
index += 1
node = Node(data)
node.next = p.next
p.next = node
# 單鏈表的刪除(刪除第 s 個結點)
def DeleteList(self, s):
if self.IsEmpty() or s < 0 or s > self.LengthList():
print("Delete failed! ")
return
p = self.head
index = 1
while index < s:
pre = p
index += 1
p = p.next
pre.next = p.next
p = None
# 單鏈表的讀取(獲取第 s 個結點的值)
def GetList(self, s):
if self.IsEmpty() or s < 0 or s > self.LengthList():
print("Read failed! ")
return
p = self.head
index = 1
while index < s:
index += 1
p = p.next
print("第 {} 個值為 {}".format(s, p.data))
更多內容,歡迎關注公眾號「Python空間」,期待和你的交流。