題目描述

Sylvia 是一個熱愛學習的女孩子。

前段時間，Sylvia 參加了學校的軍訓。眾所周知，軍訓的時候需要站方陣。

Sylvia 所在的方陣中有n×mn \times mn×m名學生，方陣的行數為 nnn，列數為 mmm。

為了便於管理，教官在訓練開始時，按照從前到後，從左到右的順序給方陣中 的學生從 1 到 n×mn \times mn×m 編上了號碼（參見後面的樣例）。即：初始時，第 iii 行第 jjj 列 的學生的編號是(i−1)×m+j(i-1)\times m + j(i−1)×m+j。

然而在練習方陣的時候，經常會有學生因為各種各樣的事情需要離隊。在一天 中，一共發生了 qq q件這樣的離隊事件。每一次離隊事件可以用數對(x,y)(1≤x≤n,1≤y≤m)(x,y) (1 \le x \le n, 1 \le y \le m)(x,y)(1≤x≤n,1≤y≤m)描述，表示第 xxx 行第 yyy 列的學生離隊。

在有學生離隊後，隊伍中出現了一個空位。為了隊伍的整齊，教官會依次下達 這樣的兩條指令：

1. 向左看齊。這時第一列保持不動，所有學生向左填補空缺。不難發現在這條 指令之後，空位在第 xxx 行第 mmm 列。

2. 向前看齊。這時第一行保持不動，所有學生向前填補空缺。不難發現在這條 指令之後，空位在第 nnn 行第 mmm 列。

教官規定不能有兩個或更多學生同時離隊。即在前一個離隊的學生歸隊之後， 下一個學生才能離隊。因此在每一個離隊的學生要歸隊時，隊伍中有且僅有第 nnn 行 第 mmm 列一個空位，這時這個學生會自然地填補到這個位置。

因為站方陣真的很無聊，所以 Sylvia

注意：每一個同學的編號不會隨著離隊事件的發生而改變，在發生離隊事件後 方陣中同學的編號可能是亂序的。

輸入輸出格式

輸入格式：

輸入共 q+1q+1q+1 行。

第 1 行包含 3 個用空格分隔的正整數 n,m,qn, m, qn,m,q，表示方陣大小是 nnn 行 mmm 列，一共發 生了 qqq 次事件。

接下來 qqq 行按照事件發生順序描述了 qqq 件事件。每一行是兩個整數 x,yx, yx,y，用一個空 格分隔，表示這個離隊事件中離隊的學生當時排在第 xxx 行第 yyy 列。

輸出格式：

按照事件輸入的順序，每一個事件輸出一行一個整數，表示這個離隊事件中離隊學 生的編號。

輸入輸出樣例

輸入樣例#1： 複製

2 2 3 
1 1 
2 2 
1 2 

輸出樣例#1： 複製

1
1
4

說明

【輸入輸出樣例 1 說明】

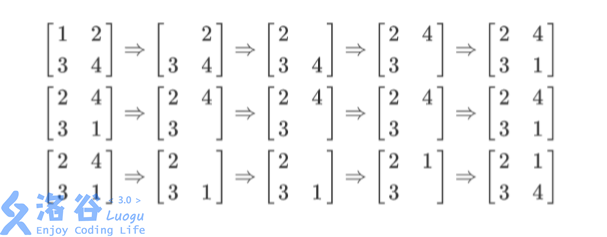
列隊的過程如上圖所示，每一行描述了一個事件。 在第一個事件中，編號為1 11 的同學離隊，這時空位在第一行第一列。接著所有同學 向左標齊，這時編號為 22 2的同學向左移動一步，空位移動到第一行第二列。然後所有同 學向上標齊，這時編號為4 4 4的同學向上一步，這時空位移動到第二行第二列。最後編號 為1 11 的同學返回填補到空位中。

【資料規模與約定】

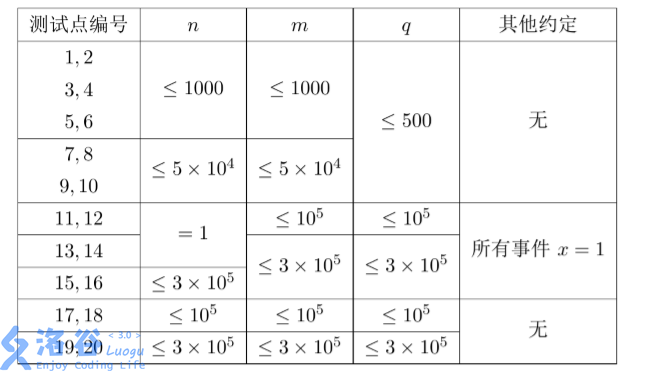
資料保證每一個事件滿足 1≤x≤n,1≤y≤m1 \le x \le n,1 \le y \le m1≤x≤n,1≤y≤m

這個題應該有不止一種做法，這裡還是用線段樹吧（貌似只會這個...orz）

這裡開n+1棵線段樹，前n棵維護n行，第n+1棵維護第m列，

分兩種情況，當y==m時，找到第n+1棵線段樹，將第x個刪除，加到第m列最後

當y!=m時，

找到第x棵線段樹，將y位置的值刪除並插入第n+1棵線段樹最後，找到第m列（即第n+1棵線段樹）中x的位置，將其刪除插入到第x棵線段樹最後。

#include<bits/stdc++.h>
#define exp 1e-8
#define mian main
#define pii pair<int,int>
#define pll pair<ll,ll>
#define ll long long
#define pb push_back
#define PI  acos(-1.0)
#define inf 0x3f3f3f3f
#define w(x) while(x--)
#define int_max 2147483647
#define lowbit(x) (x)&(-x)
#define gcd(a,b) __gcd(a,b)
#define pq(x)  priority_queue<x>
#define ull unsigned long long
#define scn(x) scanf("%d",&x)
#define scl(x) scanf("%lld",&x)
#define pl(a,n) next_permutation(a,a+n)
#define ios ios::sync_with_stdio(false)
#define met(a,x) memset((a),(x),sizeof((a)))
using namespace std;
const int maxn=6e5+10,maxm=2e7+10;
int n,m,q,Max,rt[maxn],pos,tot=0;
vector<ll>v[maxn];
struct tree{
 int sum;
 int ls,re;
}t[maxm];
void kd(int& u,int l,int r)
{
    if(!u)
        u=++tot;
    t[u].sum++;
    if(l<r){
        int mid=(l+r)>>1;
        if(mid>=pos)
            kd(t[u].ls,l,mid);
        else
            kd(t[u].re,mid+1,r);
    }
}
int query(int u,int l,int r,int k)
{
    if(l==r)
        return l;
    int mid=(l+r)>>1;
    int num=mid+1-l-t[t[u].ls].sum;
    if(num>=k)
        return query(t[u].ls,l,mid,k);
    else return query(t[u].re,mid+1,r,k-num);
}
ll workl(int x,ll w)
{
      pos=query(rt[n+1],1,Max,x);
     kd(rt[n+1],1,Max);
     ll ans=pos<=n? 1ll*m*pos:v[n+1][pos-n-1];
     v[n+1].push_back(w?w:ans);
     return ans;
}
ll workr(int x,int y)
{
     pos=query(rt[x],1,Max,y);
    kd(rt[x],1,Max);
    ll ans=pos<m? 1ll*(x-1)*m+pos:v[x][pos-m];
    v[x].push_back(workl(x,ans));
    return ans;
}
int main()
{
     while(~scanf("%d%d%d",&n,&m,&q)){
         tot=0;
        Max=q+max(n,m);
        int x,y;
        while(q--){
            scanf("%d%d",&x,&y);
            if(y==m)
               printf("%lld\n",workl(x,0));
            else
               printf("%lld\n",workr(x,y));
        }
    }
}