Time Limits: 2000 ms Memory Limits: 524288 KB

Description

院子落葉，跟我的思念厚厚一疊；窗臺蝴蝶，像詩裡紛飛的美麗章節……

Input

小 H 是一個喜歡養花的女孩子。

她買了 n 株花，編號為一里香，二里香……七里香……n 裡香，她想把這些花分別種在 n個不同的花盆裡。

對於一種方案，第 i 個花盆裡種的是 ai 裡香，小 H 定義其美麗值為：

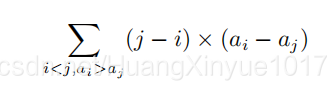
第一行一個整數 n，第二行有 n 個整數表示 {pi}。pi表示第i個花盆裡不可以種ai裡香

Output

一個整數，表示答案對 109 + 9 取模的結果。

Sample Input

3 2 1 3

Sample Output

7

Data Constraint

對於 30% 的資料，n ≤ 16。 對於 60% 的資料，n ≤ 100。 對於 100% 的資料，n ≤ 5000，{pi} 是一個排列。

Solution

• 這題嘛，DP啊……菜雞的我只會寫暴力
• 設 $f_{i,j}$ 表示一共有 $(i+j)$ 個元素，其中 $i$ 個元素有位置上的限制，$j$ 個元素沒有位置限制
• 有限制指的假定待放入元素為 $x$ ，存在位置 $p_k=x$ ，而第 $k$ 個位置還沒有填入元素
• 這樣我們就有轉移式
• $f_{0,0}=1，f_{1,0}=0，f_{0,1}=1，f_{0,2}=2$
• $f_{x,0}=(x-1)(f_{x-1,0}+f_{x-2,0})$ ……A
• $f_{x,y}=x*f_{x-1,y}+y*f_{x,y-1}$ ……B
• A式就是錯排公式，這裡的推導過程簡單清晰又自然
• B式 然後我們分情況討論
• $i$ 在 $p_j$ 上， $j$ 在 $p_i$ 上，有 $f_{n-2,0}$ 種情況，貢獻值為 $a1=$
  max(0,pj−pi)a1=max(0,p_j-p_i)
• 上面情況只滿足一個，有 $f_{n-3,1}$ 種情況，貢獻值為 $a2=(\sum{_{k=1}^{p_j-1}}k+\sum{_{k=1}^{n-p_i}}k)-2*a1$ （分別考慮 $j$ 在 $p_i$ 和 $i$ 在 $p_j$ 的情況減去 $i,j$ 同時在 $p_j,p_i$ 的情況）
• 兩個條件都不滿足，有 $f_{n-4,2}$ 種情況，貢獻值為 $\sum{_{i=2}^n\frac{i*(i-1)}{2}}-a1-a2-\sum{_{k=1}^{p_i-1}k}-\sum{_{k=1}^{n-p_j}k}+max(0,p_i-p_j)$
• 所以答案為 $\sum{_{j>i}(j-i)*(a1*f_{n-2,0}+a2*f_{n-3,1}+a3*f_{n-4,2})}$

Code

#include<algorithm>
#include<cstdio>

#define fo(i,a,b) for(int i=a;i<=b;++i)
#define fd(i,a,b) for(int i=a;i>=b;--i)
#define ll long long 

using namespace std;

const int N=5010,P=1e9+9;
int n,p[N];
ll f[N][3];

int main()
{
	freopen("derangement.in","r",stdin);
	freopen("derangement.out","w",stdout);
	scanf("%d",&n);
	fo(i,1,n) scanf("%d",&p[i]);
	f[0][0]=1,f[1][0]=0,f[0][1]=1,f[0][2]=2;
	fo(x,2,n) f[x][0]=(x-1)*(f[x-1][0]+f[x-2][0])%P;
	fo(x,1,n)
		fo(y,1,2)
			f[x][y]=(x*f[x-1][y]%P+y*f[x][y-1]%P)%P;
	ll s=0,ans=0;
	fo(i,2,n) s=(s+(i*(i-1)/2)%P)%P;
	fo(i,1,n)
		fo(j,i+1,n)
		{
			ll a1,a2,a3;
			a1=max(0,p[j]-p[i]);
			a2=(p[j]*(p[j]-1)/2)%P;
			a2=(a2+((1+n-p[i])*(n-p[i])/2)%P)%P;
			a2=((a2-2*a1)%P+P)%P;
			a3=((s-a1-a2)%P+P)%P;
			a3=((a3-(p[i]*(p[i]-1)/2)%P)%P+P)%P;
			a3=((a3-((1+n-p[j])*(n-p[j])/2)%P)%P+P)%P;
			a3=a3+max(0,p[i]-p[j]);
			ans=(ans+(j-i)*(a1*f[n-2][0]%P+a2*f[n-3][1]%P+a3*f[n-4][2]%P)%P)%P;
		}
	printf("%d",ans);
}