凸函式、凹函式判定、Jensen 不等式
阿新 • • 發佈:2018-12-18
最近看到 EM 演算法,其中的證明有用到琴生不等式,在這裡做一個筆記。
在剛開始學習凸函式和凹函式的時候,我們會被凸函式和凹函式的命名所困擾,命名看起來是凹的,一些教材上卻偏偏說它是凸函式。其實這個只是一個定義,它叫什麼,並不影響函式本身的性質。就像我在 B 站上看到有些人戲稱三國時期的武將趙雲為“雲妹”,你叫他“雲姐”“雲媽”都不會改變趙雲純爺們的形象。因此大可不必為凸函式凹函式的命名所糾結,應該結合凸函式、凹函式的性質來記憶。
例1:函式
的影象如下:
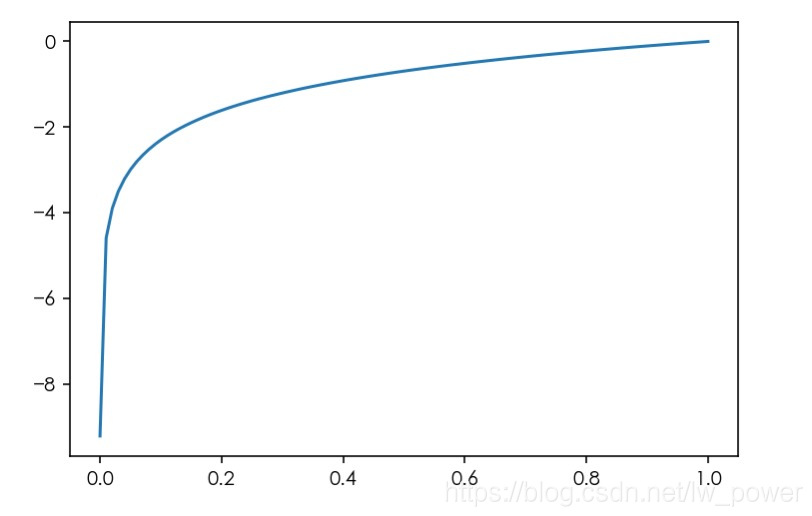
我們暫時先別糾結它叫什麼。我們看這個函式有什麼性質,和 Jensen 不等式又有什麼關係。
從函式影象上,我們可以看出,這個函式是逐漸上升的,這個函式的一階導數 也說明了 是增函式。
我們知道,導函式的增減性說明了函式的凹凸性,如果我們知道函式的凹凸性,就能夠確定區域性極值就是全域性最優值。
而導函式的增減性,就是二階導數。我們可以畫出各個點的切線,看看切線的斜率變化,就知道二階導數的增減性了。很容易知道,切線的斜率是越來越小的,因此,導函式的導函式是減函式,從函式的表示式上也很容易驗證。
那麼 Jensen 不等式又說了什麼呢?對於 Jensen 不等式的兩點形式來說,就是圖中任意兩點的之間的部分都在這兩點的割線的上方,即:
用概率論期望的語言解釋就是:
應用於多個點,就是:
其中 ,。
把 KaTeX parse error: Expected 'EOF', got '\logx' at position 8: f(x) = \̲l̲o̲g̲x̲ 應用到上面,就是
其中 ,。 這就是《統計學習方法》P159 腳註 1 的內容。
