可是還是覺得不過癮，還有下面的情況需要對比。於是就有了這篇博文。

案例：

想要基於有限樣本數來確定他的頻譜。

下面我們分如下幾種情況來分別討論：

a. 求出並畫出  的DTFT；

b. 求出並畫出  的DTFT；

clc;clear;close all;

n = 0:99;
x = cos(0.48*pi*n) + cos(0.52*pi*n);

n1 = 0:9;
y1 = x(1:10);

subplot(2,2,1)
stem(n1,y1);
title('signal x(n), 0 <= n <= 9');
xlabel('n');ylabel('x(n) over n in [0,9]');
Y1 = dft(y1,10);
magY1 = abs(Y1);
k1 = 0:1:9;
N = 10;
w1 = (2*pi/N)*k1;

subplot(2,2,2);
% stem(w1/pi,magY1);
% title('DFT of x(n) in [0,9]');
% xlabel('frequency in pi units');

%In order to clearly see the relationship between DTFT and DFT, we draw DTFT on the same picture.


%Discrete-time Fourier Transform
K = 500;
k = 0:1:K;
w = 2*pi*k/K; %plot DTFT in [0,2pi];
X = y1*exp(-j*n1'*w);

magX = abs(X);
% hold on 
plot(w/pi,magX);

% hold off






subplot(2,2,3)
stem(n,x);
title('signal x(n), 0 <= n <= 99');
xlabel('n');ylabel('x(n) over n in [0,99]');
Xk = dft(x,100);
magXk = abs(Xk);
k1 = 0:1:99;
N = 100;
w1 = (2*pi/N)*k1;

subplot(2,2,4);
% stem(w1/pi,magXk);
% title('DFT of x(n) in [0,99]');
% xlabel('frequency in pi units');

%In order to clearly see the relationship between DTFT and DFT, we draw DTFT on the same picture.


%Discrete-time Fourier Transform
K = 500;
k = 0:1:K;
w = 2*pi*k/K; %plot DTFT in [0,2pi];
X = x*exp(-j*n'*w);

magX = abs(X);

hold on 
plot(w/pi,magX);

hold off


 

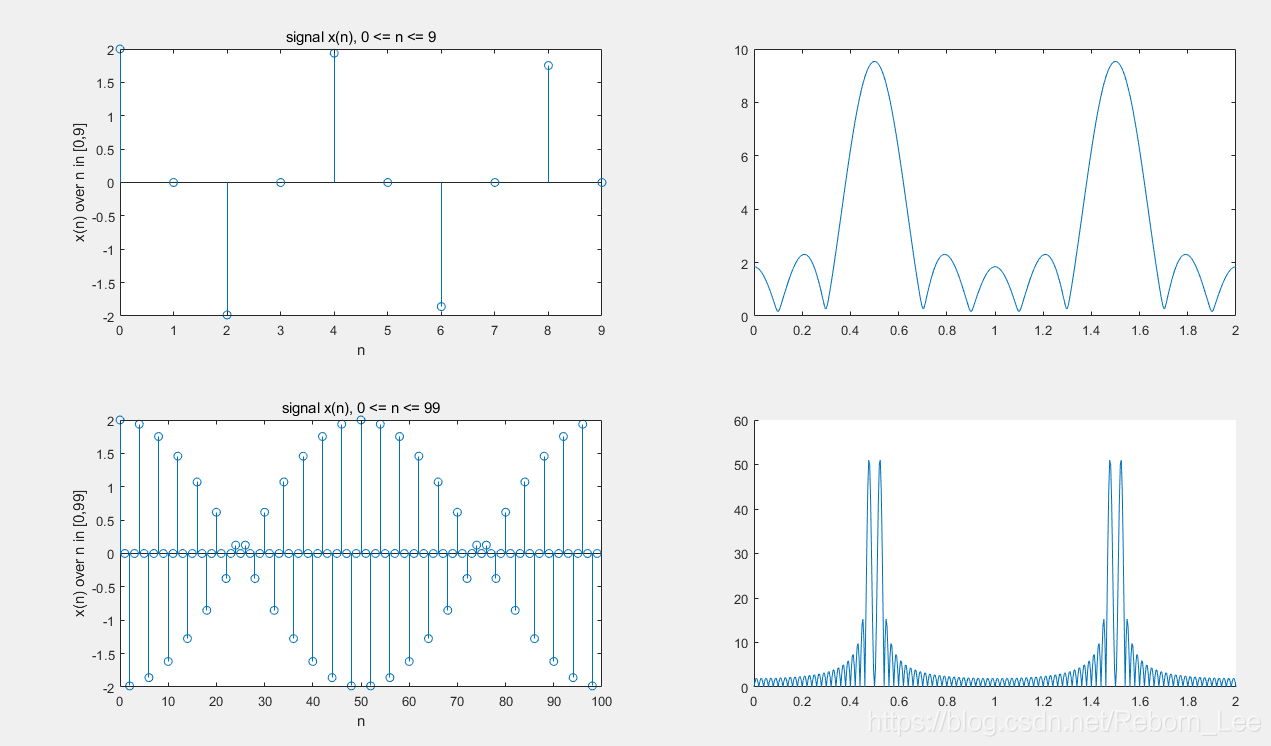
可見，b問這種情況，擁有x(n)的更多資料，所以得到的DTFT更加的準確，正如我們所料，頻譜在w = 0.48pi以及0.52pi處取得峰值。而a問中的圖就看不出這種關係，因為獲得序列資料太少，已經嚴重影響到了頻譜的形狀。