MVG學習筆記(5) --四檢視幾何和n檢視重建
四檢視幾何和n檢視重建
可以使用基於張量的方法再進行一步,並定義四個檢視中可見的四焦點張量相關實體。 然而這種方法很少使用,因為計算符合其內部約束的四焦點張量的相對困難。
然而,它確實提供了基於四個檢視計算投影重建的非迭代方法。 然而,張量方法不會擴充套件到超過四個檢視,因此從四個以上的檢視重建變得更加困難。
從幾種觀點考慮了許多方法進行重建,我們考慮了其中的一些方法。 一種方法是使用三檢視或雙檢視技術逐位重建場景。 這種方法可以應用於任何影象序列,並且在選擇要使用的正確三元組時要小心,但是它通常會成功。
有些方法可以在特定情況下使用。 如果我們能夠應用更簡單的相機模型(稱為仿射相機,affine camera),則重建的任務變得更容易。 每當到場景的距離與場景的背面和正面之間的深度差異相比較大時,該相機模型就是透視投影的公平近似。
如果在涉及仿射相機的所有個檢視中都可以看到一組點,那麼可以使用眾所周知的演算法(因式分解演算法,factorization algorithm)來計算場景的結構,以及使用在一個步驟中使用奇異值分解得到的特定相機模型。
該演算法非常可靠且易於實現。 它的主要困難是使用仿射相機模型,而不是完整的射影(投影)模型,以及要求所有點在所有檢視中都可見。
該方法已經在稱為投影分解(projective factorization)的方法中擴充套件到投影相機。 雖然這種方法通常令人滿意,但無法證明在所有情況下都能收斂到正確的解決方案。 此外,它還要求所有點在所有影象中都可見。
用於檢視重建的其他方法涉及各種假設,例如假設在所有檢視中可見的世界中的四個共麵點,或者在序列中的所有影象中可見的六個或七個點。 還開發了適用於特定運動序列的方法,例如線性運動,平面運動或單軸(轉盤)運動。
一般重建問題的主要方法是捆綁調整(bundle adjustment,BA)。 這是一種迭代方法,其中人們試圖將非線性模型擬合到測量資料(點對應關係)。 BA的優點在於它是一種非常通用的方法,可以應用於廣泛的重建和優化問題。 它可以用這樣的方式實現,即所發現的解決方案是問題的最大似然解決方案,該解決方案在某種意義上就影象測量的不準確性的模型而言是最優的。
不幸的是,BA是一個迭代過程,不能保證從任意起始點收斂到最優解。 大量對重建方法的研究,尋求易於計算的可用作BA的起點非最優解
一個共同的印象是BA必然是一種緩慢的技術。 事實是,當實現時會發現它是非常有效的,而且現如今很多SFM和SLAM領域採用了BA,以後有機會則弄個博文描述該技術。
使用檢視重建技術,可以從相當長的影象序列自動執行重建。 下圖給出了一個例子,顯示了700幀的重建。
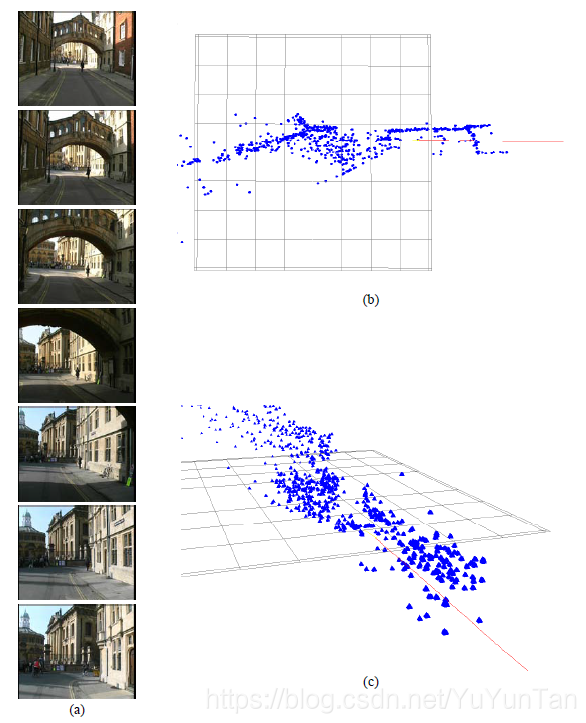
圖1,重建。 (a)手持相機在牛津街上行走時獲得的700幀序列的七幀。 (b)(c)重建點雲和攝像機路徑(紅色曲線)的兩個檢視。 圖由David Capel和2d3(www.2d3.com)提供。
