迴歸分析往往是學統計、學計量課程時接觸的第一個統計模型了，甚至不少人可能認為迴歸分析理所當然成為計量的絕大部分內容——畢竟很多教材中提到統計模型的時候，往往就一個 OLS 為主的講法。迴歸分析的內容當然很廣泛，也在學科中佔據相對基礎的位置。

學會 OLS，有人還明白了 ML 等方法的含義；現在學統計分析的時候，或多或少會安排統計軟體的實踐課程，於是大家學會了使用 Excel，乃至 SAS 中如何來做經典的迴歸分析。看過不少的文獻，很多都忽略了迴歸分析模型診斷這個環節——可能很多標準教科書沒有強調，甚至是沒有講；這不能不說是一個遺憾。

迴歸分析使用最廣泛，誤用的情況也多了些。下面使用一個經典的例子，來 “噁心” 一下那些 “過分鐘愛” 經典迴歸分析的人——我在很多課堂上都舉過這個例子（Anscombe），作為從基礎課程向中級乃至高階課程的開場白。

x1 x2 x3 x4    y1   y2    y3    y4
1  10 10 10  8  8.04 9.14  7.46  6.58
2   8  8  8  8
 
  6.95 8.14  6.77  5.76
3  13 13 13  8  7.58 8.74 12.74  7.71
4   9  9  9  8  8.81 8.77  7.11  8.84
5  11 11 11  8  8.33 9.26  7.81  8.47
6  14 14 14  8  9.96 8.10  8.84  7.04
7
 
   6  6  6  8  7.24 6.13  6.08  5.25
8   4  4  4 19  4.26 3.10  5.39 12.50
9  12 12 12  8 10.84 9.13  8.15  5.56
10  7  7  7  8  4.82 7.26  6.42  7.91
11  5  5  5  8  5.68 4.74  5.73  6.89

上面有四對 x，y，分別做經典迴歸分析的話，結果如下：

[[1]]
Estimate Std. Error  t value    Pr(>|t|)
(Intercept) 3.0000909  1.1247468 2.667348 0.025734051
x1          0.5000909  0.1179055 4.241455 0.002169629
[[2]]
Estimate Std. Error  t value    Pr(>|t|)
(Intercept) 3.000909  1.1253024 2.666758 0.025758941
x2          0.500000  0.1179637 4.238590 0.002178816
[[3]]
Estimate Std. Error  t value    Pr(>|t|)
(Intercept) 3.0024545  1.1244812 2.670080 0.025619109
x3          0.4997273  0.1178777 4.239372 0.002176305
[[4]]
Estimate Std. Error  t value    Pr(>|t|)
(Intercept) 3.0017273  1.1239211 2.670763 0.025590425
x4          0.4999091  0.1178189 4.243028 0.002164602

這時候你會發現 p 值、s.e. 值都好的很，截距項和斜率項也非常好，甚至連 R square 都簡直一模一樣。

往往講到這個時候，機靈點的學生就開始皺眉頭了：資料差別挺大的，怎麼模型都是一樣呢！？

學過迴歸診斷的人立刻就嚷嚷來做個迴歸診斷來看看，四種情況下是不是有的屬於 “模型前提假設” 不滿足的情況。（當然，似乎本科階段，教師沒有過分強調這點的，很少有學生能自己自主的想到這點，所以往往讓人感嘆教學過程中的不完善。）

緊接著我就給他們做出一幅圖：

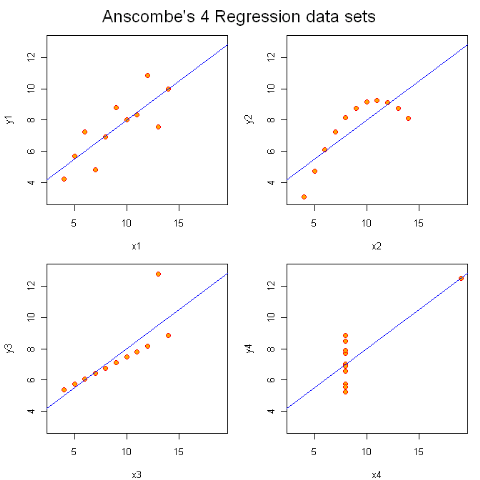
這時候他們有點明白，能回答說左上是我們 “常見” 的迴歸；右上完全就是二次曲線嘛；左下存在一個 “異常點”；而右下，完全就屬於“詭異” 情形。

所以可以歸納一下：做統計模型的時候，一定記得要模型診斷下——重點就分析下殘差是不是符合假設——這個是標準套路。如果你想 “偷懶”，在只有一個自變數的時候，不妨在樣本量不多（現在的統計軟體已經非常強大了，數萬對點很容易搞定；如果資料太多，你也可以抽樣來試試嘛。）這樣，“一眼” 就能看出個大概了——這恐怕就是人比機器厲害的地方，人比模型厲害的地方。