前言：

特徵值分解： 其中Q是這個矩陣A的特徵向量組成的矩陣，Σ是一個對角陣，每一個對角線上的元素就是一個特徵值。

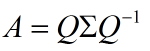
特徵值分解可以得到特徵值與特徵向量，特徵值表示的是這個特徵到底有多重要，而特徵向量表示這個特徵是什麼，可以將每一個特徵向量理解為一個線性的子空間，我們可以利用這些線性的子空間幹很多的事情。不過，特徵值分解也有很多的侷限，比如說變換的矩陣必須是方陣。 

一、奇異值

奇異值分解是一個能適用於任意的矩陣的一種分解的方法，可以說和特徵值分解的思路一脈相承。

假設A是一個N * M的矩陣，那麼得到的U是一個N * N的方陣（裡面的向量是正交的，U裡面的向量稱為左奇異向量），Σ是一個N * M的矩陣（除了對角線的元素都是0，對角線上的元素稱為奇異值），V’(V的轉置)是一個N * N的矩陣，裡面的向量也是正交的，V裡面的向量稱為右奇異向量）

前10%甚至1%的奇異值的和就佔了全部的奇異值之和的99%以上了。也就是說，我們也可以用前r大的奇異值來近似描述矩陣，這裡定義一下部分奇異值分解：

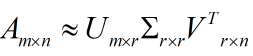
r是一個遠小於m、n的數。

二、對奇異值的理解

本質上，奇異值就是對矩陣進行特徵提取，就和人一樣評價一個事物的時候，會尋找事物最本質的特徵。機器學習演算法亦是如此，奇異值分解就是把原始矩陣表達為更小的矩陣。