概述 

IrregIsotropicBRDF 和 RegularHalfangleBRDF 的作用 :

（利用測量的資料來模擬 表面的反射，例如：其實就是在類中儲存了BRDF的很多采樣點，根據wi,wo 來對 獲得取樣點之間的插值之後的資料，這些資料就是對應的BRDF值）

Using measured data about the reflection properties of real surfaces is one of the most effective approaches for rendering realistic materials. One way to do so is to use the measured data to set the parameter values for a parameterized BRDF like the Torrance– Sparrow model.

However, parameterized BRDF models are often not flexible enough to model the full complexity of scattering characteristics of many interesting surfaces. If accurate measured reflection data is available for a surface of interest, then directly using it for rendering can faithfully(如實地) re-create the surface’s appearance.

In this section, we’ll implement BxDFs that interpolate sampled BRDF values directly. While this is a memory-intensive(記憶體密集型) approach for scenes that use many different measured BRDFs, it works well for reflection distributions that don’t fit analytic models well and can provide a reference for comparison to other approaches.

Rendering with measured BRDF data does have challenges. It can be difficult to make adjustments for artistic purposes.If there is excessive error in the data, results may be poor as well: especially for highly specular and anisotropic surfaces, the 4D BRDF must be densely sampled, leading to a large amount of data to store and many measurements to be taken. Finally, BRDFs may have considerable variation in their values, which adds to the challenges of acquiring accurate BRDF data sets.

Measured BRDF data may come in one of two forms: as regularly spaced tabularized(列成表格) data, or as a large number of irregularly spaced individual samples. Regularly spaced data makes efficient lookups possible. (For example, if we have a 4D table of values for an anisotropic BRDF, indexed by (θi , φi , θo, φo), then, given a pair of directions, we just need to index into the table and interpolate between the values.) However, it can be difficult to acquire BRDF values with such a regular spacing. Acquiring good measurements for directions close to the horizon can be particularly difficult, for example. Irregular sample spacings avoid these issues, though are not as easy to use for rendering. (Irregular sets of BRDF samples are often resampled in a preprocess to generate a set of regular samples.)

Therefore, pbrt has implementations of two BxDFs for using measured reflection data for rendering. The first, IrregIsotropicBRDF interpolates from irregularly spaced samples of isotropic BRDFs. The second, RegularHalfangleBRDF, supports the regular sampling used byMatusik et al.’s data set (2003a, 2003b). Both of these are used by the MeasuredMaterial defined in Section 9.2.4.

IrregIsotropicBRDF 類

class IrregIsotropicBRDF : public BxDF {
public:
    // IrregIsotropicBRDF Public Methods
    IrregIsotropicBRDF(const KdTree<IrregIsotropicBRDFSample> *d)
        : BxDF(BxDFType(BSDF_REFLECTION | BSDF_GLOSSY)), isoBRDFData(d) { }
    Spectrum f(const Vector &wo, const Vector &wi) const;
private:
    // IrregIsotropicBRDF Private Data
    const KdTree<IrregIsotropicBRDFSample> *isoBRDFData;
};

類的作用：

（IrregIsotropicBRDF  中儲存 不規則的 各向同性 的BRDF的取樣點，給一對(wi,wo)的話，就會根據這對方向去取樣點陣列中找到最適合的BRDF取樣值，利用這些取樣值進行外掛得到最終的BRDF值 ）

IrregIsotropicBRDF supports irregularly sampled isotropic BRDF data. Given a pair of directions, it finds a few BRDF samples that are nearby in the space of incident and outgoing directions and interpolates between their values, based on how close they are to the actual directions.

1. 建構函式

IrregIsotropicBRDF(const KdTree<IrregIsotropicBRDFSample> *d)
        : BxDF(BxDFType(BSDF_REFLECTION | BSDF_GLOSSY)), isoBRDFData(d) { }

const KdTree<IrregIsotropicBRDFSample> *isoBRDFData;

細節：

a.

（用 面的公式來表示一個BRDF的取樣點）

Point BRDFRemap(const Vector &wo, const Vector &wi);
struct IrregIsotropicBRDFSample {
    IrregIsotropicBRDFSample(const Point &pp, const Spectrum &vv)
        : p(pp), v(vv) { }
    IrregIsotropicBRDFSample() { }
    Point p;
    Spectrum v;
};

Point BRDFRemap(const Vector &wo, const Vector &wi) {
    float cosi = CosTheta(wi), coso = CosTheta(wo);
    float sini = SinTheta(wi), sino = SinTheta(wo);
    float phii = SphericalPhi(wi), phio = SphericalPhi(wo);
    float dphi = phii - phio;
    if (dphi < 0.) dphi += 2.f * M_PI;
    if (dphi > 2.f * M_PI) dphi -= 2.f * M_PI;
    if (dphi > M_PI) dphi = 2.f * M_PI - dphi;
    return Point(sini * sino, dphi / M_PI, cosi * coso);
}

We’d therefore like to use a mapping function for isotropic BRDFs that takes a 4D pair of directions ωi and ωo and converts them into a point in a three-dimensional space such that the distance between two points is meaningful, the isotropy of the BRDF is reflected, and reciprocity is represented. For the IrregIsotropicBRDF, we’ll implement a mapping proposed by Marschner, denoted by φ3 in his thesis(Marschner 1998; Section 5.6.3):

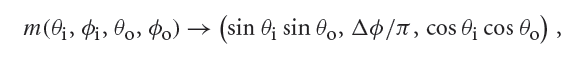
where  Δφ = (φi − φo), and Δφ is remapped to be in the range [0, π]. (Thanks to the isotropy assumption, Δφ values in [π, 2π] are equivalent to 2π − Δφ, which is in [0, π].)

This mapping accounts for isotropy and reciprocity, and the distance between two three tuples in the mapping’s range has a meaningful relationship to the distance between their respective pairs of directions. The BRDFRemap() function implements this mapping.

b.

（用 kd-tree 來儲存BRDF的取樣值）

When a IrregIsotropicBRDF is created by the MeasuredMaterial::GetBSDF() method, it is given a pointer to a three-dimensional kd-tree that stores the BRDF samples, where the sample positions are represented with the values returned by BRDFRemap(). Note that this kd-tree is managed by the MeasuredMaterial and is only used for lookups (i.e., in a read-only manner) by the code here.

2. 

Spectrum f(const Vector &wo, const Vector &wi) const;

作用：

（利用wo，wi，來重構一個 point出來，就利用 point 去 kd-tree 來查詢 多個 取樣點 ，再進行加權平均，求出平均值作為 BRDF的值）

The IrregIsotropicBRDF::f() method first remaps the given pair of directions and then performs a series of kd-tree lookups, searching with a progressively wider search radius for nearby points until a few samples have been found. In general, it’s preferable to smoothly interpolate between a few BRDF samples rather than just find the single closest sample for the lookup here.

細節：

Spectrum IrregIsotropicBRDF::f(const Vector &wo,
                               const Vector &wi) const {
    Point m = BRDFRemap(wo, wi);
    float lastMaxDist2 = .001f;
    while (true) {
        // Try to find enough BRDF samples around _m_ within search radius
        IrregIsoProc proc;
        float maxDist2 = lastMaxDist2;
        isoBRDFData->Lookup(m, proc, maxDist2);
        if (proc.nFound > 2 || lastMaxDist2 > 1.5f)
            return proc.v.Clamp() / proc.sumWeights;
        lastMaxDist2 *= 2.f;
    }
}

struct IrregIsoProc {
    // IrregIsoProc Public Methods
    IrregIsoProc() { sumWeights = 0.f; nFound = 0; }
    void operator()(const Point &p, const IrregIsotropicBRDFSample &sample,
                    float d2, float &maxDist2) {
        float weight = expf(-100.f * d2);
        v += weight * sample.v;
        sumWeights += weight;
        ++nFound;
    }
    Spectrum v;
    float sumWeights;
    int nFound;
};

a.

IrregIsoProc is the callback structure used by the KdTree::Lookup() method for each sample within the search radius. (The squared search radius is provided to the Lookup() method in maxDist2.) If not enough points are found, the squared search distance is doubled, and another lookup is performed.

IrregIsoProc processes each BRDF sample within the search radius, accumulating a weighted sum of samples close to the lookup point.

BRDF sample values are weighted with an ad hoc exponential(指數) falloff based on the squared distance between the lookup point and the sample point. The sum of these weights is accumulated so that the final value can be normalized.