DZY Loves Fibonacci Numbers CodeForces
阿新 • • 發佈:2018-12-19
二次剩餘:
斐波那契通項公式:
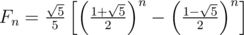
先打表求出根號5在模1e9+9意義下的數。
然後就化簡成立區間加上等比數列的形式,維護每段區間加了多少次等比數列就行。
下面我們來看如何維護一個等比數列。假如我對區間[L,R]的加上1,2,4,8...2^n的話,那麼我只需要加一個標記x表示這個區間被加了多少次這樣的2^n.
舉個例子 [1,8] 上加一個等比數列,我只需要x+=1,就可以了,當我的區間往下傳的時候,[1,4]這個區間的x+=1,[5,8]這個區間x+=2^4*1
這個利用的就是公比相同的數列相加仍然是等比數列的性質。求和利用的則是 a1(q^n-1)/(q-1),所以只需要預處理出q-1的逆元還有q^n我們就可以根據區間資訊很快的求出和了。
在本題中 q-1的逆=q,首項也是q,所以前n項和就是 qi^(n+2)-qi^2(i=1,2). 其實主要就是考慮怎麼維護等比數列的問題。
程式碼:(有問題)
#include <bits/stdc++.h> using namespace std; const int maxn=3e5+7; typedef long long ll; const int mod=1e9+7; ll bas = 276601605; ll q1 = 691504013; ll q2 = 308495997; int n,m; int a[maxn]; struct Tree { int l,r; ll a,b,sum; }tree[maxn<<1]; #define Lson l,m,rt<<1 #define Rson m+1,r,rt<<1|1 ll qpow(ll a,ll b) { ll ans=1; while(b) { if(b&1) { ans=ans*a%mod; } a=a*a%mod; b>>=1; } return ans; } ll mul1[maxn],mul2[maxn]; void init() { mul1[0]=1,mul2[0]=1; for(int i=1;i<=maxn+4;i++) { mul1[i]=mul1[i-1]*q1%mod; mul2[i]=mul2[i-1]*q2%mod; } } void push_up(int rt) { tree[rt].sum=(tree[rt<<1].sum+tree[rt<<1|1].sum)%mod; } void push_down(int rt) { int a=tree[rt].a,b=tree[rt].b; int len1=tree[rt<<1].r-tree[rt].l+1; int len2=tree[rt<<1|1].r-tree[rt<<1|1].l+1; if(a||b) { tree[rt<<1].a=(tree[rt<<1].a+a)%mod; tree[rt<<1|1].a=(tree[rt<<1|1].a+a*mul1[len1])%mod; tree[rt<<1].b=(tree[rt<<1].b+b)%mod; tree[rt<<1|1].b=(tree[rt<<1|1].b+b*mul2[len2])%mod; tree[rt<<1].sum=(tree[rt<<1].sum+a*(mul1[len1+2]-mul1[2])%mod)%mod; tree[rt<<1].sum=(tree[rt<<1].sum-b*(mul2[len1+2]-mul2[2])%mod+mod)%mod; tree[rt<<1|1].sum=(tree[rt<<1|1].sum+a*mul1[len1]%mod*(mul1[len2+2]-mul1[2])%mod)%mod; tree[rt<<1|1].sum=(tree[rt<<1|1].sum-b*mul2[len1]%mod*(mul2[len2+2]-mul2[2])%mod+mod)%mod; tree[rt].a=tree[rt].b=0; } } void Build(int l,int r,int rt) { tree[rt].l=l,tree[rt].r=r; tree[rt].a=tree[rt].b=0; if(l==r) { tree[rt].sum=0; return; } int m=(l+r)>>1; Build(Lson); Build(Rson); push_up(rt); } void updata(int L,int R,ll ad,ll ac,int l,int r,int rt) { if(L<=l&&R>=r) { tree[rt].a+=1; tree[rt].b+=1; int len=tree[rt].r-tree[rt].l+1; tree[rt].sum=(tree[rt].sum+ad*(mul1[len+2]-mul1[2])%mod)%mod; tree[rt].sum=(tree[rt].sum-ac*(mul2[len+2]-mul2[2])%mod+mod)%mod; return; } int m=(l+r)>>1; push_down(rt); if(L<=m) { updata(L,R,ad,ac,Lson); } if(R>m) { int len1=tree[rt<<1].r-tree[rt<<1].l+1; updata(L,R,ad*mul1[len1],ac*mul2[len1],Rson); } push_up(rt); } ll query(int L,int R,int l,int r,int rt) { if(L<=l&&R>=r) { return tree[rt].sum; } int m=(r+l)>>1; push_down(rt); ll ans=0; if(L<=m) { ans=(ans+query(L,R,Lson))%mod; } if(R>m) { ans=(ans+query(L,R,Rson))%mod; } push_up(rt); return ans; } ll sum[maxn]; int main() { #ifndef ONLINE_JUDGE freopen("in.txt","r",stdin); freopen("out.txt","w",stdout); #endif init(); scanf("%d%d",&n,&m); sum[0]=0; for(int i=1;i<=n;i++) { scanf("%d",&a[i]); sum[i]=sum[i-1]+a[i]; } Build(1,n,1); while(m--) { int op,l,r; scanf("%d%d%d",&op,&l,&r); if(op==1) { updata(l,r,1,1,1,n,1); } else { ll ans=query(l,r,1,n,1)*bas%mod; printf("%lld\n",ans); //printf("%lld\n",ans+sum[r]-sum[l-1]); } } return 0; }
程式碼(正確的):
#pragma warning(disable:4996) #include <iostream> #include <cstdio> #include <cstring> #include <string> #include <vector> #include <cmath> #include <algorithm> using namespace std; #define ll long long #define mod 1000000009 #define maxn 300500 ll bas = 276601605; ll q1 = 691504013; ll q2 = 308495997; ll xx5 = 383008016; ll inv5 = 200000002; ll inv2 = 500000005; ll invq1; ll invq2; ll pow_mod(ll a, ll n){ ll ret = 1; while (n){ if (n & 1) ret = ret*a%mod; n >>= 1; a = a*a%mod; } return ret; } ll a[maxn], b[maxn]; int n, m; ll val[maxn]; ll sum[maxn]; struct Node { int l, r; ll ax, bx; ll sum; }N[maxn << 2]; void build(int i, int L, int R){ N[i].l = L; N[i].r = R; N[i].ax = N[i].bx = N[i].sum = 0; if (L == R){ return; } int M = (L + R) >> 1; build(i << 1, L, M); build(i << 1 | 1, M + 1, R); } void pushDown(int i){ ll av = N[i].ax, bv = N[i].bx; if (N[i].ax != 0 || N[i].bx != 0){ N[i << 1].ax = (N[i << 1].ax + av) % mod; N[i << 1].bx = (N[i << 1].bx + bv) % mod; int len = N[i << 1].r - N[i << 1].l + 1; N[i << 1 | 1].ax = (N[i << 1 | 1].ax + av*a[len] % mod) % mod; N[i << 1 | 1].bx = (N[i << 1 | 1].bx + bv*b[len] % mod) % mod; int len2 = N[i << 1 | 1].r - N[i << 1 | 1].l + 1; N[i << 1].sum = (N[i << 1].sum + av*(((a[len + 2] - a[2]) % mod + mod) % mod) % mod) % mod; N[i << 1].sum = (N[i << 1].sum - bv*(((b[len + 2] - b[2]) % mod + mod) % mod) % mod) % mod; N[i << 1 | 1].sum = (N[i << 1 | 1].sum + av*a[len] % mod*(a[len2 + 2] - a[2] + mod) % mod) % mod; N[i << 1 | 1].sum = ((N[i << 1 | 1].sum - bv*b[len] % mod*(b[len2 + 2] - b[2] + mod) % mod) % mod + mod) % mod; N[i].ax = N[i].bx = 0; } } void pushUp(int i){ N[i].sum = (N[i << 1].sum + N[i << 1 | 1].sum) % mod; } void update(int i, int L, int R, ll x, ll y){ if (N[i].l == L&&N[i].r == R){ N[i].ax = (N[i].ax + x) % mod; N[i].bx = (N[i].bx + y) % mod; int len = R - L + 1; N[i].sum = (N[i].sum + x*(a[len + 2] - a[2] + mod) % mod + mod) % mod; N[i].sum = (N[i].sum - y*(b[len + 2] - b[2] + mod) % mod + mod) % mod; return; } pushDown(i); int M = (N[i].l + N[i].r) >> 1; if (R <= M){ update(i << 1, L, R, x, y); } else if (L > M){ update(i << 1 | 1, L, R, x, y); } else{ int len = (M - L + 1); update(i << 1, L, M, x, y); update(i << 1 | 1, M + 1, R, a[len] * x%mod, b[len] * y%mod); } pushUp(i); } ll query(int i, int L, int R){ if (N[i].l == L&&N[i].r == R){ return N[i].sum; } pushDown(i); int M = (N[i].l + N[i].r) >> 1; if (R <= M){ return query(i << 1, L, R); } else if (L > M){ return query(i << 1 | 1, L, R); } else{ return (query(i << 1, L, M) + query(i << 1 | 1, M + 1, R)) % mod; } pushUp(i); } int main() { scanf("%d%d", &n, &m); a[0] = b[0] = 1; for (int i = 1; i <= n + 5; i++){ a[i] = a[i - 1] * q1%mod; b[i] = b[i - 1] * q2%mod; } val[0] = 0; sum[0] = 0; for (int i = 1; i <= n; i++){ scanf("%I64d", val + i); sum[i] = (sum[i - 1] + val[i]) % mod; } build(1, 1, n); int oper, l, r; for (int i = 0; i < m; i++){ scanf("%d%d%d", &oper, &l, &r); if (oper == 1) update(1, l, r, 1, 1); else { ll res = query(1, l, r); res = (res + mod) % mod; res = res*bas%mod; res = (res + ((sum[r] - sum[l - 1]) % mod+mod)%mod) % mod; printf("%I64d\n", res); } } return 0; }


