深度學習入門—理論雜談(2)
阿新 • • 發佈:2018-12-19
前言
當我們對某些事情出現嚴重錯誤時,我們人類往往學得最快。但是人工神經元在嚴重錯誤的情況下學習是很困難的。更重要的是,事實證明,這種行為不僅發生在簡單模型中,而且還發生在更一般的網路中。為什麼學習這麼慢?我們能找到避免這種放緩的方法嗎?
一、交叉熵成本函式
為了解決在異常情況下,二次成本函式(即基於最小二乘法的損失函式)學習的慢的問題,引入了交叉熵成本損失函式。
首先,我們二話不說,先放出交叉熵的公式:
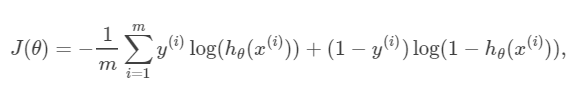 以及J(θ)對引數θ的偏導數(用於諸如梯度下降法等優化演算法的引數更新),如下:
以及J(θ)對引數θ的偏導數(用於諸如梯度下降法等優化演算法的引數更新),如下:
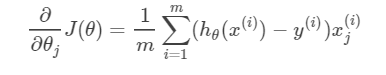 這裡就不詳細證明了,若有興趣可參考這篇不錯的部落格,證明的非常棒:https://blog.csdn.net/jasonzzj/article/details/52017438
這裡就不詳細證明了,若有興趣可參考這篇不錯的部落格,證明的非常棒:https://blog.csdn.net/jasonzzj/article/details/52017438
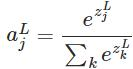
 softmax函式最明顯的特點在於:它把每個神經元的輸入佔當前層所有神經元輸入之和的比值,當作該神經元的輸出。這使得輸出更容易被解釋:神經元的輸出值越大,則該神經元對應的類別是真實類別的可能性更高。
另外,softmax不僅把神經元輸出構造成概率分佈,而且還起到了歸一化的作用,適用於很多需要進行歸一化處理的分類問題。
sigmoid函式極其導數我們都比較熟悉了,那麼softmax的導數是怎麼樣的呢? 由於softmax在ANN演算法中的求導結果比較特別,分為兩種情況。希望能幫助到正在學習此類演算法的朋友們。求導過程如下所示:
softmax函式最明顯的特點在於:它把每個神經元的輸入佔當前層所有神經元輸入之和的比值,當作該神經元的輸出。這使得輸出更容易被解釋:神經元的輸出值越大,則該神經元對應的類別是真實類別的可能性更高。
另外,softmax不僅把神經元輸出構造成概率分佈,而且還起到了歸一化的作用,適用於很多需要進行歸一化處理的分類問題。
sigmoid函式極其導數我們都比較熟悉了,那麼softmax的導數是怎麼樣的呢? 由於softmax在ANN演算法中的求導結果比較特別,分為兩種情況。希望能幫助到正在學習此類演算法的朋友們。求導過程如下所示:
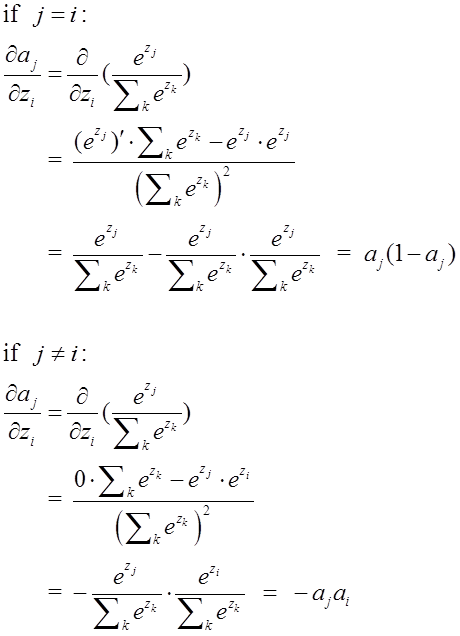
 為了檢驗softmax和這個代價函式也可以解決上述所說的訓練速度變慢問題,接下來的重點就是推導ANN的權重w和偏置b的梯度公式。以偏置b為例:
為了檢驗softmax和這個代價函式也可以解決上述所說的訓練速度變慢問題,接下來的重點就是推導ANN的權重w和偏置b的梯度公式。以偏置b為例:


