第500篇文章紀念

時間飛逝啊，我竟然已經在寫第500篇文章了 回首當年艱辛的$OI$路，再看看我目前取得的的這些成績，瞬時覺得當年那些委屈和痛苦都沒有白受 當年母親一直說我搞$OI$是個錯誤的決定，但是現在她也不這麼想了，反而很支援我搞競賽 話不多說 來看這道十分具有紀念意義的題目

題目

時間限制：1000ms；空間限制：128MB 【題目描述】 當狼群作戰時，隨著群體變大，其戰鬥力就會爆炸地增長，能產生許多奇蹟。 有一個靠狼群作戰的王國，他們擁有數不清的戰狼與士兵。目前，大敵壓境，將軍要鎮守一側的n個大門，每個大門可以佈置一個士兵或一隻戰狼，當有k個連著的大門都佈置了戰狼，這k只戰狼就會形成狼群，更容易獲勝。機智的將軍已經算好，只要有一個m只狼的狼群就有把握獲勝，當然，理論上狼群的數量與大小都是多多益善，但實際要平衡好戰狼與人的關係。 那麼問題來了，這個王國的好奇寶寶想知道理論上有多少種獲勝的佈置方案，忙碌的將軍將沒時間數，就希望你寫一個程式幫幫他。 【輸入】

兩個中間有空格的整數n，m。（1<=m<=n<=10,000,000） 【輸出】 理論上有把握獲勝的方案數。 （由於獲勝的方案數太多了，所以要將結果模10000007來滿足好奇寶寶的好奇心）

【輸入樣例】 5 3 【輸出樣例】 8 題目源自syy

題解

用$P(x)$表示$x$這個狼群的大小不小於$m$ 滿足條件的序列必然滿足如下命題 $\exist xP(x)$ 那麼不滿足條件的序列就是對上述命題取非 $\forall x\lnot P(x)$ 統計出不滿足條件的，再用總個數$2^n$減去就得到答案了 那麼現在就是要統計有多少長度為$n$

的人、狼序列，其中所有的狼群大小都嚴格小於$m$ $f_{ij}$表示長度為$i$的序列，最後連續$j$個是狼 $f_{i,0}=\sum_{j=0}^{m-1}f_{i-1,j}$ $f_{ij}(j&gt;0)=f_{i-1,j-1}$ 直接看方程不夠直觀，如果寫出整個二維陣列，我用橙色的線表示求和，如下圖 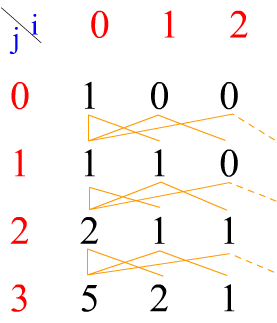其中虛線的表示更新到一個不存在的狀態 可以看到，每行的第一個數都是前一行每個數的和，而後面的數是由前一行依次向右平移得來的 每行最後一個數在平移之後會被舍掉， 但是我如果不把他舍掉，而是直接接在下一行的後面，就會產生這樣的效果： 在最後一行出現了類似於斐波那契數列的遞推形式 每一個數字都等於它前面連續$m$項的和 維護一個字首和，搞一搞就能快速求出第$N+1$項$f_{n+1}$ 答案就是$2^n-f_{n+1}$ 時間複雜度$O(n)$

程式碼

//syy的題
#include <bits/stdc++.h>
#define ll long long
#define maxn 10000010
#define mod 10000007ll
using namespace std;
ll f[maxn], s[maxn];
ll read(ll x=0)
{
	ll c, f=1;
	for(c=getchar();!isdigit(c);c=getchar())if(c=='-')f=-1;
	for(;isdigit(c);c=getchar())x=(x<<1)+(x<<3)+c-48;
	return f*x; 
}
ll fastpow(ll a, ll b)
{
	ll t=a, ans=1;
	for(;b;b>>=1,t=t*t%mod)if(b&1)ans=ans*t%mod;
	return ans;
}
void preprocess(ll n, ll m)
{
	ll i;
	f[0]=s[0]=1;
	for(i=1;i<=n+1;i++)
	{
		f[i]=s[i-1];
		if(i>=m-1)f[i]-=s[i-m-1];
		f[i]%=mod;
		s[i]=(s[i-1]+f[i])%mod;
	}
}
int main()
{
	ll N=read(), M=read(), ans=0, i;
	preprocess(N,M);
	ans=fastpow(2,N)-f[N+1];
	cout<<(ans%mod+mod)%mod;
	return 0;
}

測試資料

輸入1：
5 3
輸出1：
8

輸入2：
10  3
輸出2：
520

輸入3：
1000 10
輸出3：
8930315

輸入4：
1811 1
輸出4：
2657145

輸入5：
1991 9
輸出5：
3969738

輸入6：
190 2
輸出6：
6873368

輸入7：
83 6
輸出7：
4775625

輸入8：
8 5
輸出8：
20

輸入9：
29 4
輸出9：
5808696

輸入10：
883 2
輸出10：
2206875

輸入11：
10000000 5000000
輸出11：
8791226

輸入12：
9876543 1234567
輸出12：
7690719

輸入13：
9999979 7688907
輸出13：
4659058