1．一個奇怪的函式呼叫程式

• 問題：如何完成兩個資料的交換？
  分析：同學A和同學B如何交換雙方座位？都會輕功的話，雙方不用著地且同時朝對方的座位飛過去即可。但我們都是凡人，怎麼辦？

通過細心思考，聰明的我們發現通過以下步驟即可：

• 步驟1：同學A先離開自己的座位，找個其他地方先待著；
• 步驟2：同學B離開自己的座位，去坐在A的座位上；
• 步驟3：同學A離開待著的地方，去坐在B的座位上。
  通過這三步，雙方完成座位的交換。同理，也可以先讓B同學離開座位，效果是一樣的。

1.1 具體到程式中，如何程式設計實現兩個資料的交換？

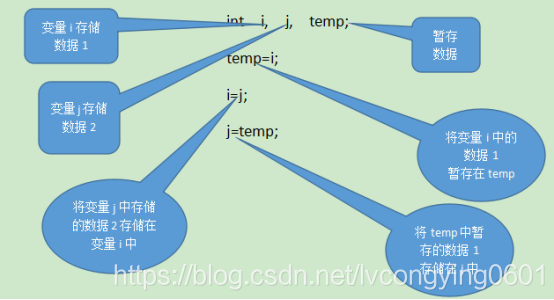
1.2 單用main來實現交換

如果單採用一個main函式來實現交換的話，程式碼如下：

#include<stdio.h>
int main()
{
	int i,j,temp;
	scanf("%d%d",&i,&j);
	temp=i;
	i=j;
	j=temp;
	printf("i=%d,j=%d\n",i,j);
	return 0;
}

i和j順利完成了交換。

1.3 採用子函式來實現交換

如果想自己定義一個子函式，來實現交換功能，該子函式則在main函式中呼叫。具體程式碼如下：

#include<stdio.h>
void swap(int a,int b) 
{
	int temp;
	temp=a;
	a=b;
	b=temp;
}
int main()
{
	int i,j;
	scanf("%d%d",&i,&j);
    swap(i,j);
	printf("after:i=%d,j=%d\n",i,j);
	return 0;
}
 

分析：主函式main中通過swap(i,j)對子函式swap進行了呼叫，i把它的值傳給了swap的a，j把它的值傳給了swap的b，通過稱i和j為實參，稱a和b為形參。然後，在swap中完成了a和b的交換。接下來，執行輸出語句printf的時候會發生什麼呢？為什麼呢？該如何修改程式呢？
出現問題的主要原因是：區域性變數（區域性變數的作用域和生存期引發的）。
既然有區域性變量了，就會有全域性變數，二者有和區別？同學們可以自行思考下。
修改該程式有兩個方法：（1）指標；（2）C++裡面的引用。
感興趣的可查閱資料，這部分內容上課講述。
此外，編寫好一個子函式，其目的就是讓呼叫它，因為子函式被呼叫了，它的程式碼才能被執行，函式功能才能得以體現。函式的呼叫方法有很多，較為重要的有：巢狀呼叫和遞迴呼叫。

2. 函式的巢狀呼叫

C語言中，函式的定義是獨立的，即一個函式不能定義在另一個函式內部。但在呼叫時，可以在一個函式中呼叫另一個函式，即函式1呼叫了函式2，而函式2又呼叫了函式3，這就是函式的巢狀呼叫。
例項：輸出四個資料中的最大者。
假如如下設計程式：

#include<stdio.h>
int max2(int a,int b)
{
	if(a>b)
		return a;
	else
		return b;
}
int max4(int a,int b,int c,int d)
{
	int res;
	res=max2(a,b);
	res=max2(res,c);
	res=max2(res,d);
	return res;
}
int main()
{
	int a,b,c,d,max;
	scanf("%d%d%d%d",&a,&b,&c,&d);
  max=max4(a,b,c,d);
	printf("max=%d\n",max);
	return 0;
}

分析：
該程式中，max2計算兩個資料中的最大者，max4計算四個資料中的最大者，在max4中對max2進行了呼叫。這就是巢狀呼叫。
該程式執行的流程為：
步驟1：執行main函式的開頭部分；
步驟2：遇到main函式中的max=max4(a,b,c,d)；時，中斷main函式的執行，轉到max4函式中執行；
步驟3：執行max4函式的開頭部分，遇到res=max2(a,b);時，中斷max4的執行，轉到max2中執行；
步驟4：執行max2函式，如果該函式中沒有巢狀其他函式，則完成該函式的全部操作，然後返回到max4函式中剛才呼叫max2時中斷的位置；
步驟5：繼續按照上述思想執行max4函式中尚未執行的部分；直到max4函式結束；
步驟6：當max4函式執行結束後，返回到main函式中剛才呼叫max4時中斷的位置；
步驟7：繼續按照上述思想執行main函式中尚未執行的部分，直到main函式結束。

• **拓展：函式呼叫時最多可以巢狀多少層？
• 答曰：直觀上感覺，可以無限層。很遺憾，函式可以巢狀呼叫多少層是由程式執行時一個名為“棧”的資料結構決定的。一般而言，Windows上程式的預設棧大小約為1Mbit，每一次函式呼叫至少佔用8位元組，因此粗略計算，函式呼叫大概只能巢狀約一千層，如果巢狀呼叫的函式裡包含許多變數和引數，實際值要遠遠小於這個數目。
  當然，單純手動書寫程式碼寫出一千層巢狀函式呼叫基本是不可能的，但是通過“遞迴”的方法就可以輕鬆達到這個上限。**

3. 函式的遞迴呼叫

前面計算1+2+3+…+n的方法：用迴圈實現逐次相加。其實，這類問題也可以通過函式的遞迴呼叫來實現。
什麼是函式的遞迴呼叫？也即一個函式間接或直接呼叫自身的過程。遞迴演算法的實質是將原有問題分解為新的問題，而解決新問題時又用到了原有問題的解法。按照這一原則分解下去，每次出現的新問題都是原有問題的簡化的子集，而最終分解出來的問題，是一個已知的問題，這便是有限的遞迴呼叫。
遞迴的過程有兩個階段：
第一階段：遞推。將原問題不斷分解為新的子問題，逐漸從未知向已知推進，最終達到已知的條件，即遞迴結束的條件，這時遞推階段結束。
例如，求1+2+3+4+5，可以這樣分解：
1+2+3+4+5=(1+2+3+4)+5——>1+2+3+4=(1+2+3)+4——>(1+2+3)=(1+2)+3——>1+2=(1)+2——>1=1
第二階段：迴歸。從已知的條件出發，按照遞推的逆過程，逐一求值迴歸，最後達到遞推的開始處，結束迴歸階段，完成遞迴呼叫。

遞推不能是無限的，否則無法迴歸，所以遞迴呼叫必須有結束條件，不然會陷入無限的狀態，永遠無法結束呼叫。
例項1：先講一下課本上的常用例子吧。求n!
在前面，針對該問題，我們採用了迴圈語句來實現的。其實，也可以採用遞迴來實現該問題。

#include<stdio.h>
unsigned fac(unsigned n)
{
	unsigned f;
	if(n==0)
		f=1;
	else
		f=fac(n-1)*n;
	return f;
}
int main()
{
	unsigned n;
	scanf("%u",&n);
	printf("%u!=%u\n",fac(n));
	return 0;
}

注意：對同一個函式的多次不同調用中，編譯器會為函式的形參和區域性變數分配不同的空間，它們互不影響。例如，在執行fac(2)時呼叫fac(1)，編譯器會用1為被調函式fac的形參n初始化，但不會改變主調函式fac中的形參n的值2。當fac(1)返回後，主調函式fac中的形參值仍然為2，同理，區域性變數f也一樣。
例項2：採用遞迴呼叫來計算1+2+3+…+n。具體程式如下：

#include<stdio.h>
int GetSum(int n)
{
	if(n==1)
		return 1;
	else
		return GetSum(n-1)+n;
}
int main()
{
	int m;
	scanf("%d",&m);
	printf("%d\n",GetSum(m));
	return 0;
}

例項3：設有一對新生兔子，從第3個月開始，它們每個月都生一對兔子，新生的兔子也如此繁殖。假設兔子沒有死亡，問一年後，共有多少兔子？
在前面，針對該問題，我們採用的迭代的方法來解決的。經過前面的分析，我們知道：
第3個月的兔子對數=第2個月的兔子對數+第1個月的兔子對數（因為第1個月的兔子在第3個月時開始生寶寶了）。
同理，第4個月的兔子對數=第3個月的兔子對數+第2個月的兔子對數（因為第2個月的兔子在第4個月時開始生寶寶了）。
同理，第5個月的兔子對數=第4個月的兔子對數+第3個月的兔子對數（因為第3個月的兔子在第6個月時開始生寶寶了）。
。。。
依次類推，可知這是一個遞迴問題，month月的兔子總數等於month-1月的兔子數+month-2月的兔子數。

#include<stdio.h>
int RabNum(int month)
{
	if(month==1||month==2)
		return 1;
	return RabNum(month-1)+RabNum(month-2);
}
int main()
{
	int month=12;
	printf("%d\n",RabNum(month));
	return 0;
}

例項4：遞迴呼叫的神奇應用——解決漢諾塔問題！
有一個梵塔，塔內有3個座A、B和C，最初時A座上有64個盤子，盤子大小不等，大的在下，小的在上。要求把這64個盤子從A座移到C座，在移到過程中可以藉助B座，每次只允許移動一個盤子，且在移到過程中始終保持大盤在下，小盤在上。請程式設計實現移動的過程。
分析：假如A座上有3個盤子，可以通過：
A——>C，A——>B，C——>B，A——>C，B——>A，B——>C，A——>C這7個步驟來實現移動。
假如是更多盤子呢，我們該怎麼移動，假如是n個盤子呢？這個步驟將異常複雜。但採用遞迴的思想可以輕易實現。可通過3步來完成：
步驟1：將A座上的n-1個盤子藉助C座移動到B座上；
步驟2：將A座上剩下的1個盤子移到C座上；
步驟3：將B座上的n-1個盤子藉助A座移到C座上。

#include<stdio.h>
void move(char src,char dest)
{
	printf("%c-->%c\t",src,dest);
}
void hanoi(int n,char a,char b,char c)
{
	if(n==1)
		move(a,c);
	else
		{
			hanoi(n-1,a,c,b);
			move(a,c);
			hanoi(n-1,b,a,c);
		}
}
int main()
{
	int n;
	scanf("%d",&n);
	hanoi(n,'A','B','C');
	return 0;
}

問題：計算一下把n個盤子從A座移到C座所需的移動次數是多少？
分析：當n=1時，只需把盤子從A座移到C座，則f(1)=1;
當n=2時，將A座上面的那個盤子移到B座，然後將A座下面的那個盤子移到C座，最後將B座上的盤子再移到C座，則f(2)=3；
當n=3時，A——>C，A——>B，C——>B，A——>C，B——>A，B——>C，A——>C這7個步驟來實現移動，即f(3)=7
…
依次類推，可以得到如下規律：f(n)=2*f(n-1)+1

#include<stdio.h>
int getNum(int n)
{
	if(n==1)
		return 1;
	else
		return 2*getNum(n-1)+1;
}
int main()
{
	int n,num;
	scanf("%d",&n);
	num=getNum(n);
	printf("%dpierce needs %d\n",n,num);
	return 0;
}