Bump Mapping：

（理想中，要做的是 根據法線，偏移一個 點 p，例如，p‘  = p + d(p)n(p)，但是，實際上，PBRT不想修改物體的幾何資訊，而是直接計算 一條新的法線來 來達到偏移的效果）

All of the Materials defined in the previous section take an optional float texture map that defines a displacement at each point on the surface: each point p has a displaced point p’ associated with it, defined by p‘  = p + d(p)n(p), where d(p) is the offset returned by the displacement texture at p and n(p) is the surface normal at p (Figure 9.6).We would like to use this texture to compute shading normals so that the surface appears as if it actually had been offset by the displacement function, without modifying its geometry. This process is called bump mapping.

Figure 9.6: A displacement function associated with a material defines a new surface based on the old one, offset by the displacement amount along the normal at each point. pbrt doesn’t compute a geometric representation of this displaced surface, but instead uses it to compute shading normals for bump mapping.

Bump Mapping 的推導：

1. The implementation of Material::Bump() is based on finding an approximation to the partial derivatives ∂p/∂u and ∂p/∂v of the displaced surface and using them in place of the surface’s actual partial derivatives to compute the shading normal. (Recall that the surface normal is given by the cross product of these vectors, n = ∂p/∂u×∂p/∂v.)

（基本的思路就是，計算 偏移之後的 ∂p‘/∂u and ∂p’/∂v，利用 n =∂p'/∂u×∂p'/∂v, 計算 新的法線出來）

2. Assume that the original surface is defined by a parametric function p(u, v), and thebump offset function is a scalar function d(u, v). Then the displaced surface is given by

where n(u, v) is the surface normal at (u, v).

（上面公式的就是 計算一個偏移後的點 p'）

3. The partial derivatives of this function can be found using the chain rule. For example, the partial derivative in u is

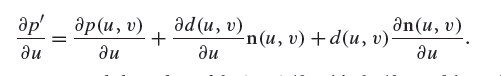
We already have computed the value of ∂p(u, v)/∂u; it’s ∂p/∂u and is available in the DifferentialGeometry structure, which also stores the surface normal n(u, v) and the partial derivative ∂n(u, v)/∂u = ∂n/∂u. The displacement function d(u, v) can be evaluated as needed, which leaves ∂d(u, v)/∂u as the only unknown term.

（對 p' 對 u 的偏導數，得到的上面的公式，觀察上面的公式可以知道，只有 ∂d(u, v)/∂u 是未知項，其他都是已知的，

其實對於 p' 對 v 的偏導數，得到的其他的公式也是類似的，得到的是  ∂d(u, v)/∂v 是未知項，其他都是已知的，

例如 ： ）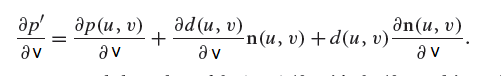

4. 計算  ∂d(u, v)/∂u 和  ∂d(u, v)/∂v

Recall the definition of the partial derivative:

Forward differencing approximates the value using a finite value of Δu and evaluating d(u, v) at two positions. Thus, the final expression for ∂p‘/∂u is the following (for simplicity, we have dropped the explicit dependence on (u, v) for some of the terms):

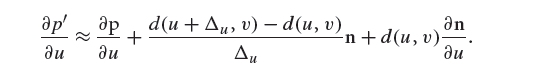
（變換下∂d(u, v)/∂u的表達形式得到最後計算∂p‘/∂u公式就是上面的，∂p‘/∂v 也是類似的，觀察上面的公式，

總結下，計算 ∂p‘/∂u 需要首先計算的 d(u + Δu，v) 和 Δu, 計算 ∂p‘/∂v 需要首先計算 d(u，v + Δv) 和 Δv）

static void Bump(const Reference<Texture<float> > &d, const DifferentialGeometry &dgGeom,         const DifferentialGeometry &dgShading, DifferentialGeometry *dgBump);

void Material::Bump(const Reference<Texture<float> > &d,
                    const DifferentialGeometry &dgGeom,
                    const DifferentialGeometry &dgs,
                    DifferentialGeometry *dgBump) {
    // Compute offset positions and evaluate displacement texture
    DifferentialGeometry dgEval = dgs;

    // Shift _dgEval_ _du_ in the $u$ direction
    float du = .5f * (fabsf(dgs.dudx) + fabsf(dgs.dudy));
    if (du == 0.f) du = .01f;
    dgEval.p = dgs.p + du * dgs.dpdu;
    dgEval.u = dgs.u + du;
    dgEval.nn = Normalize((Normal)Cross(dgs.dpdu, dgs.dpdv) +
                          du * dgs.dndu);
    float uDisplace = d->Evaluate(dgEval);

    // Shift _dgEval_ _dv_ in the $v$ direction
    float dv = .5f * (fabsf(dgs.dvdx) + fabsf(dgs.dvdy));
    if (dv == 0.f) dv = .01f;
    dgEval.p = dgs.p + dv * dgs.dpdv;
    dgEval.u = dgs.u;
    dgEval.v = dgs.v + dv;
    dgEval.nn = Normalize((Normal)Cross(dgs.dpdu, dgs.dpdv) +
                          dv * dgs.dndv);
    float vDisplace = d->Evaluate(dgEval);
    float displace = d->Evaluate(dgs);

    // Compute bump-mapped differential geometry
    *dgBump = dgs;
    dgBump->dpdu = dgs.dpdu + (uDisplace - displace) / du * Vector(dgs.nn) +
                   displace * Vector(dgs.dndu);
    dgBump->dpdv = dgs.dpdv + (vDisplace - displace) / dv * Vector(dgs.nn) +
                   displace * Vector(dgs.dndv);
    dgBump->nn = Normal(Normalize(Cross(dgBump->dpdu, dgBump->dpdv)));
    if (dgs.shape->ReverseOrientation ^ dgs.shape->TransformSwapsHandedness)
        dgBump->nn *= -1.f;

    // Orient shading normal to match geometric normal
    dgBump->nn = Faceforward(dgBump->nn, dgGeom.nn);
}

細節：

a. 

// Shift _dgEval_ _du_ in the $u$ direction     float du = .5f * (fabsf(dgs.dudx) + fabsf(dgs.dudy));     if (du == 0.f) du = .01f;     dgEval.p = dgs.p + du * dgs.dpdu;     dgEval.u = dgs.u + du;     dgEval.nn = Normalize((Normal)Cross(dgs.dpdu, dgs.dpdv) +                           du * dgs.dndu);     float uDisplace = d->Evaluate(dgEval);

作用：

這裡主要就是計算   d(u + Δu，v) 和 Δu， 構造一個 DifferentialGeometry dgEval，這個 dgEval.p, dgEval.u, dgEval.nn 其實都是往 u方向偏移過的，之後 傳入 dgEval 給 d Texture，就可以計算得到   d(u + Δu，v)

b.

float dv = .5f * (fabsf(dgs.dvdx) + fabsf(dgs.dvdy));     if (dv == 0.f) dv = .01f;     dgEval.p = dgs.p + dv * dgs.dpdv;     dgEval.u = dgs.u;     dgEval.v = dgs.v + dv;     dgEval.nn = Normalize((Normal)Cross(dgs.dpdu, dgs.dpdv) +                           dv * dgs.dndv);     float vDisplace = d->Evaluate(dgEval);

作用：

這裡的主要是計算  d(u，v + Δv)  和 Δv， 和上面基本一致

c.

 *dgBump = dgs;     dgBump->dpdu = dgs.dpdu + (uDisplace - displace) / du * Vector(dgs.nn) +                    displace * Vector(dgs.dndu);     dgBump->dpdv = dgs.dpdv + (vDisplace - displace) / dv * Vector(dgs.nn) +                    displace * Vector(dgs.dndv);     dgBump->nn = Normal(Normalize(Cross(dgBump->dpdu, dgBump->dpdv)));

作用：

這裡就是利用公式計算  ∂p‘/∂u and ∂p’/∂v，之後 利用 ∂p‘/∂u and ∂p’/∂v 來計算新的法線。

d.

if (dgs.shape->ReverseOrientation ^ dgs.shape->TransformSwapsHandedness)         dgBump->nn *= -1.f;

    // Orient shading normal to match geometric normal     dgBump->nn = Faceforward(dgBump->nn, dgGeom.nn);

作用：

Finally, this method flips the shading coordinate frame if needed, so that the shading normal lies in the hemisphere around the geometric normal. Since the shading normal represents a relatively small perturbation(擾亂) of the geometric normal, the two of them should always be in the same hemisphere.