2. 程式人生 > >吳恩達 deep learning 第三週 淺層神經網路

吳恩達 deep learning 第三週 淺層神經網路

阿新 • • 發佈：2018-12-19

文章目錄

神經網路概覽

[]表示不同的層
x (

i ) x^{(i)} 表示第i個數據

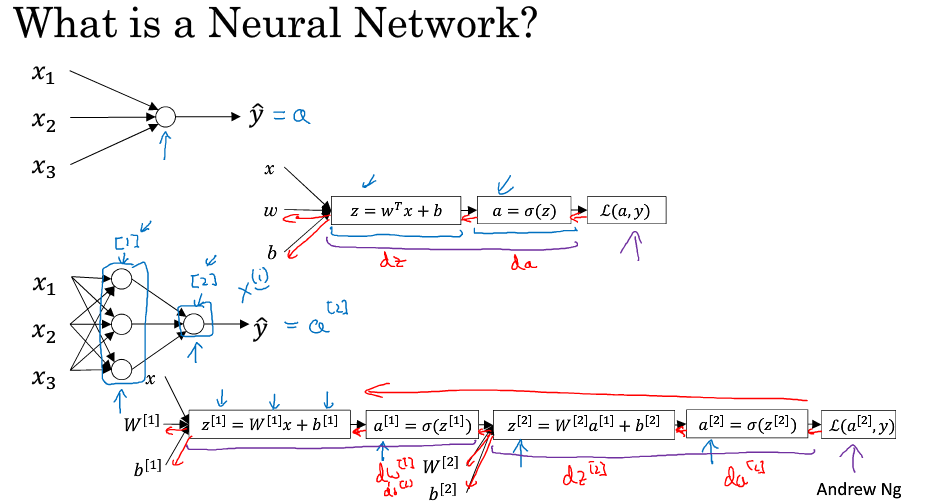
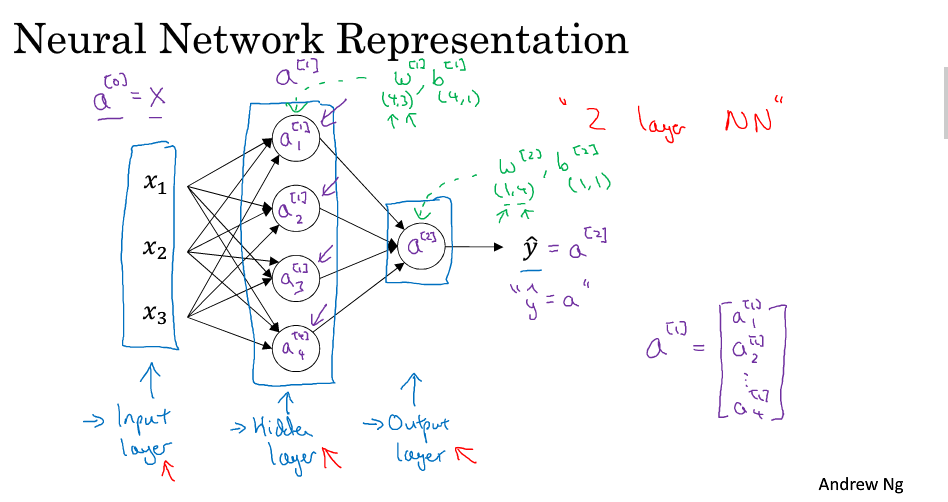
神經網路的表示

簡單的神經網路
a [ i

] a^{[i]} 表示第i層的啟用值
w [ i ]
， b [ i ] w^{[i]} ，b^{[i]} 表示第i層的引數
w [ 1 ] w^{[1]} 是4*3的矩陣，4表示4個隱藏單元，3表示3個輸入

計算神經網路的輸出

神經網路的計算過程

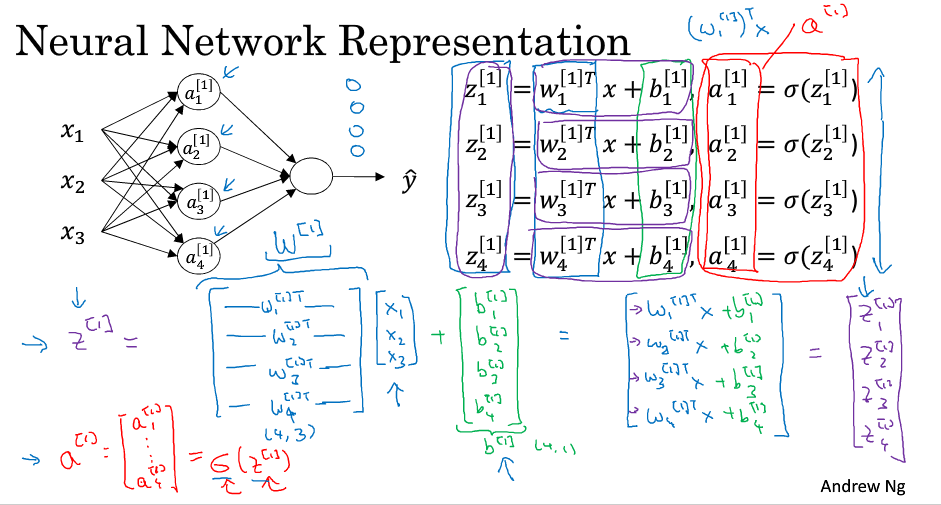
向量化之後的計算過程

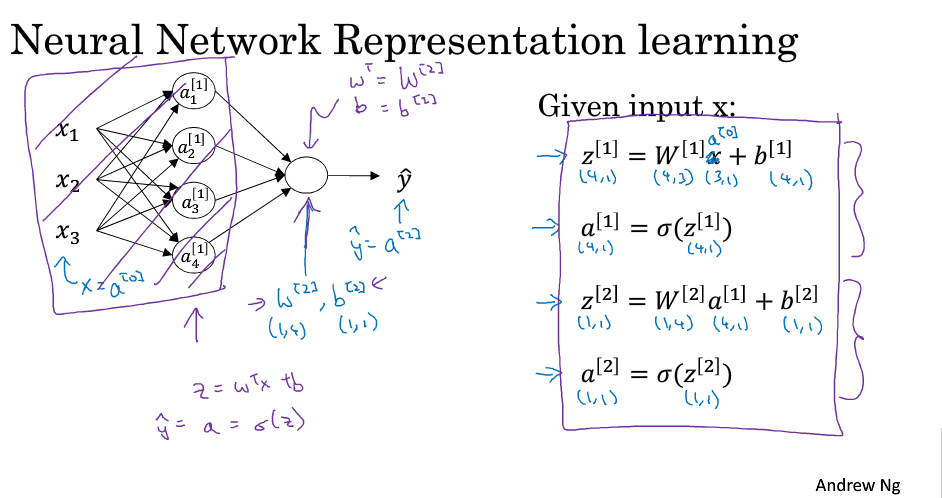
多個例子中的向量化

向量化的實現，通過向量化可以更快的實現神經網路的計算

啟用函式

幾種不同的啟用函式

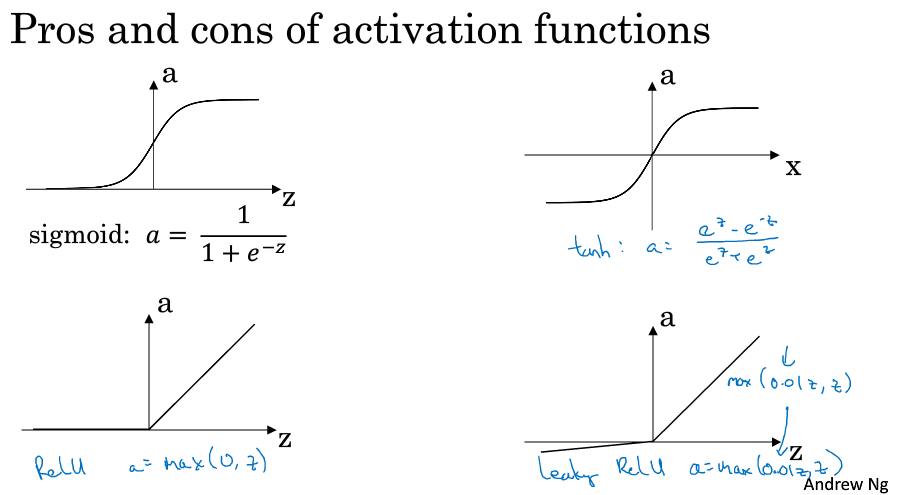
tanh啟用函式幾乎在所有場合由於sigmoid，在做二分類的時候，輸出層使用sigmoid函式
tanh和sigmoid有一個缺點就是如果z很大或者很小，那麼導數的梯度可能就會很小，這就會導致梯度下降很慢
ReLU 修正性單元 缺點是當z為負的時候，導數等於零
Leaky ReLU 解決上述問題 這兩者的優點是啟用函式的斜率和0差得很遠，在實踐中使用ReLU啟用函式，神經網路的訓練會快很多，雖然ReLU有一半的斜率為0，當有足夠多的隱藏單元，令z>0

為什麼需要非線性啟用函式


如果使用線性啟用函式，那麼神經網路只是把輸入線性組合在輸出

啟用函式的導數

Sigmoid函式的導數

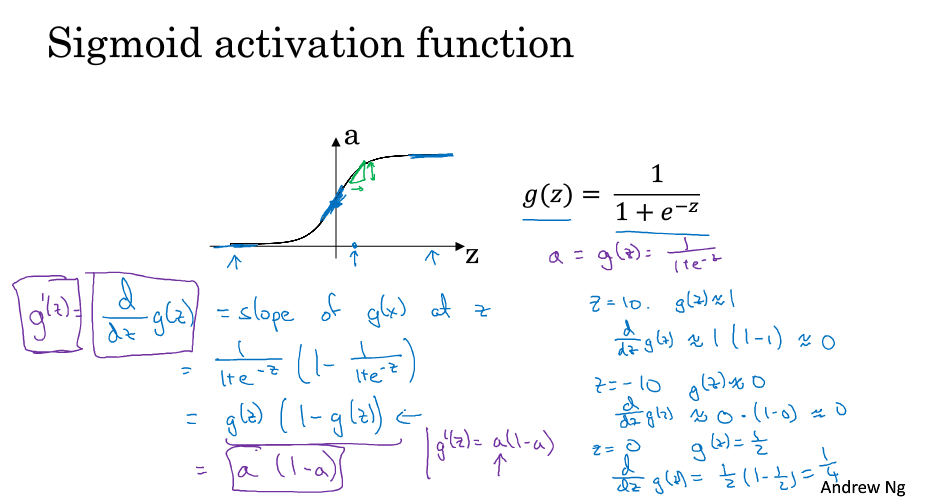
Tanh函式的導數

ReLU和Leaky ReLu導數

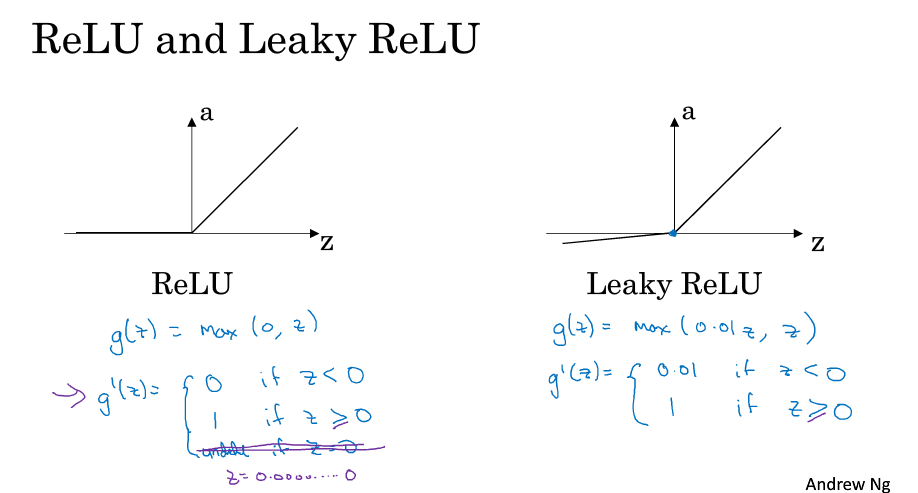
神經網路的梯度下降

神經網路梯度下降

正向傳播和反向傳播
keepdims=True 保證輸出的是矩陣

隨機初始化

當隱藏單元的引數設定為0時，通過多次迭代隱藏單元還是對稱的，都在計算完全一樣的函式，這樣多個隱藏單元沒有意義

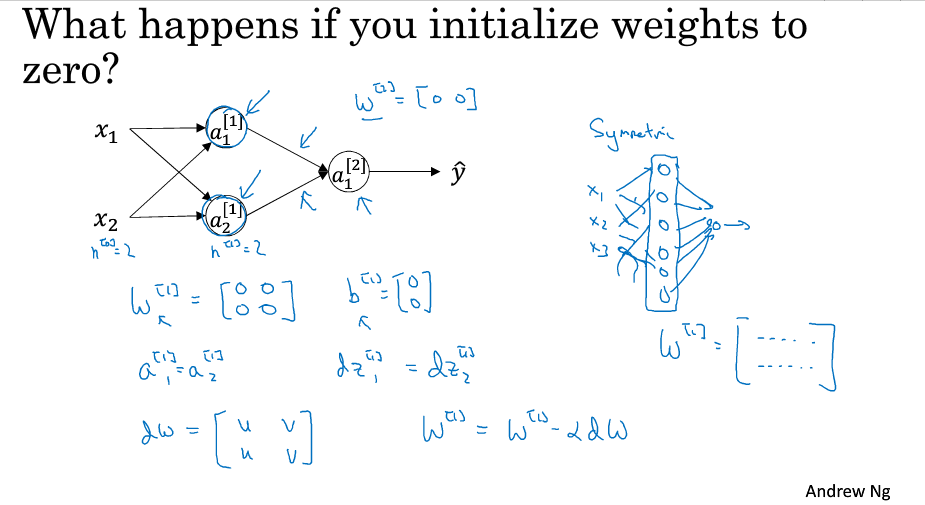
將w*0.01是為了儘可能的是輸出小，使得z的值位於sigmoid和tanh啟用函式的0附近，0附近的梯度較大，可以提高神經網路的速度

相關推薦

吳恩達 deep learning 第三週 淺層神經網路

文章目錄 神經網路概覽 神經網路的表示 計算神經網路的輸出 多個例子中的向量化 啟用函式 為什麼需要非線性啟用函式 啟用函式的導數 神經網路的梯度下降

吳恩達deep learning筆記第二課 改善深層神經網路：超引數除錯、正則化以及優化

學習吳恩達DL.ai第二週視訊筆記。 1.深度學習實用層面 在訓練集和驗證集來自相同分佈的前提下，觀察訓練集的錯誤率和驗證集的錯誤率來判斷過擬合（high variance高方差）還是欠擬合（high bias高偏差）. 比如訓練集錯誤率1%，驗證集11%則過擬合（

Coursera 吳恩達 Deep Learning 第2課 Improving Deep Neural Networks 第一週 程式設計作業程式碼 Regularization

2 - L2 Regularization # GRADED FUNCTION: compute_cost_with_regularization def compute_cost_with_reg

Coursera 吳恩達 Deep Learning 第2課 Improving Deep Neural Networks 第一週 程式設計作業程式碼 Initialization

2 - Zero initialization # GRADED FUNCTION: initialize_parameters_zeros def initialize_parameters_z

吳恩達 機器學習 第三週

轉載https://www.cnblogs.com/LoganGo/p/8562575.html 一.邏輯迴歸問題（分類問題） 生活中存在著許多分類問題，如判斷郵件是否為垃圾郵件；判斷腫瘤是惡性還是良性等。機器學習中邏輯迴歸便是解決分類問題的一種方法。 二分類：通常表示為yϵ{0,1}

機器學習 | 吳恩達機器學習第三週程式設計作業(Python版)

實驗指導書  下載密碼:fja4 本篇部落格主要講解，吳恩達機器學習第三週的程式設計作業，作業內容主要是利用邏輯迴歸演算法(正則化)進行二分類。實驗的原始版本是用Matlab實現的，本篇部落格主要用Python來實現。   目錄 1.實驗包含的檔案 2.使用邏

機器學習 | 吳恩達機器學習第三週學習筆記

第三週PPT彙總下載連結:https://pan.baidu.com/s/101uY5KV_2i3Ey516DYma_A  密碼:8o4e 上一篇部落格主要介紹了第二週的課程的內容，包括多變數線性迴歸，使用梯度下降法求解多變數線性迴歸的實用技巧，特徵縮放與模型特徵選擇並

深度學習-吳恩達第一課第三週課程作業

第二週的課程作業是利用邏輯迴歸來訓練一個分類器來辨別一張圖片是否為貓，這周老師講了單隱層的神經網路，所以先看看利用這個模型能否在上次作業的基礎上對訓練準確度作出改善 訓練一個神經網路 神經網路分為幾層，隱藏層中包含幾個神經元，使用的啟用函式 初始化引數 W（i）和

tensorflow+ tutorial 吳恩達第二課第三週作業

TensorFlow Tutorial Welcome to this week's programming assignment. Until now, you've always used numpy to build neural networks. Now we will step you

吳恩達機器學習第四次作業：神經網路

這是習題和答案的下載地址，全網最便宜，只要一積分哦~~~ 這是我總結的網課裡有關神經網路的筆記，不要積分的~~~ 0.綜述      神經網路的練習，比work3part2更加全面，包括了反向傳播，顯示隱藏層，引數正確性的驗證等幾個方面。      指令碼太長

吳恩達 deep learning 第二課第二週程式設計 optimization

Optimization Methods Until now, you've always used Gradient Descent to update the parameters and minimize the cost. In this notebook, you will learn

吳恩達 deep learning 第二課第一週 程式設計作業一

  Initialization Welcome to the first assignment of "Improving Deep Neural Networks". Training your neural network requires specifying an i

Coursera-吳恩達-機器學習-第十週-測驗-Large Scale Machine Learning

本片文章內容： Coursera吳恩達機器學習課程，第十週 Large Scale Machine Learning 部分的測驗，題目及答案截圖。 1.cost increase ，說明資料diverge。減小learning rate。 stochastic不需要每步都是減

Coursera-吳恩達-機器學習-第六週-測驗-Machine Learning System Design

說實話，這一次的測驗對我還是有一點難度的，為了刷到100分，刷了7次（哭）。 無奈，第2道和第4道題總是出錯，後來終於找到錯誤的地方，錯誤原因是思維定式，沒有動腦和審題正確。 這兩道題細節會在下面做出講解。 第二題分析：題意問，使用大量的資料，在哪兩種情況時

Coursera-吳恩達-機器學習-第五週-程式設計作業: Neural Networks Learning

本次文章內容： Coursera吳恩達機器學習課程，第五週程式設計作業。程式語言是Matlab。 學習演算法分兩部分進行理解，第一部分是根據code對演算法進行綜述，第二部分是程式碼。 0 Introduction  在這個練習中，將應用 backpropagation

Coursera 吳恩達 Deep Learning 第二課 改善神經網路 Improving Deep Neural Networks 第二週 程式設計作業程式碼Optimization methods

Optimization Methods Until now, you’ve always used Gradient Descent to update the parameters and minimize the cost. In this notebo

吳恩達deep learning課程筆記0 Welcome

pro ron 其它 con 領域 沒有 str 如果 這樣的 1 課程概述 這是一個專項課程(Specialization)，包含5個獨立的課程。 1.1 Neural Networks and Deep Learning 了解NN的基礎，如何建立NN，如何訓練它，課程

Coursera 深度學習 吳恩達 deep learning.ai 筆記整理（3-2）——機器學習策略

新的 bsp 誤差 spa 歸納 空間 font 處理 整理 一、誤差分析 定義：有時我們希望算法能夠勝任人類能做的任務，但是當算法還沒達到人類所預期的性能時，人工檢查算法錯誤會讓你知道接下來做什麽，這也就是誤差分析 檢查，發現會把夠狗當恒，是否需要做一個項目專門處理狗

python下載吳恩達deep learning編程習題

.com user 技術分享 獲得 成功 port write int h+ 在cousera上註冊deep learning後，可下載課後習題。 1.進入編程環境後，單擊左上角的file-open，進入文件管理模式 2. 點擊紅圈文件夾進入根目錄 3. 在

吳恩達第一課第三周隨筆

imu tro 廣播 最終 表示 調用 大小 有關 使用 2.1 雙層神經網絡 圖 1 圖 2 圖1是一個雙層網絡模型，實際上有三層，但是通常把輸入層給忽略掉 稱為輸入層 註意層了，圖1層有4個節點，圖2只要1個， 所以圖1 應該是一個（4,3）的矩陣，圖2的是