吳恩達-機器學習(8)-K-Mean、PCA
文章目錄
Clustering
K-Mean Algorithm
下圖中已經有沒有標籤的點,現在需要分為兩類
進行k-Mean演算法
1、隨機選取兩個聚類中心,需要分為幾類就選取幾個聚類中心
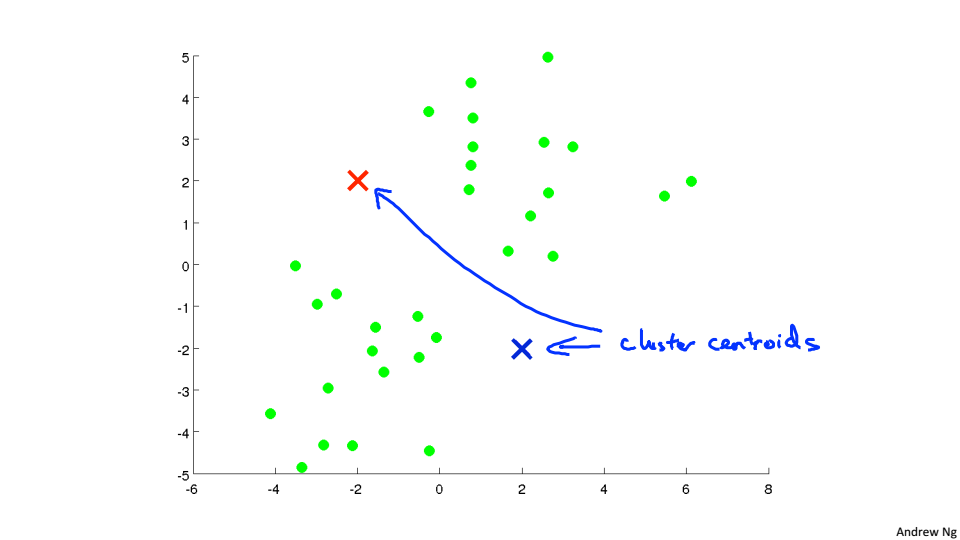
2、遍歷所有的點,根據點到聚類中心的距離來判斷將該點分到哪個聚類中
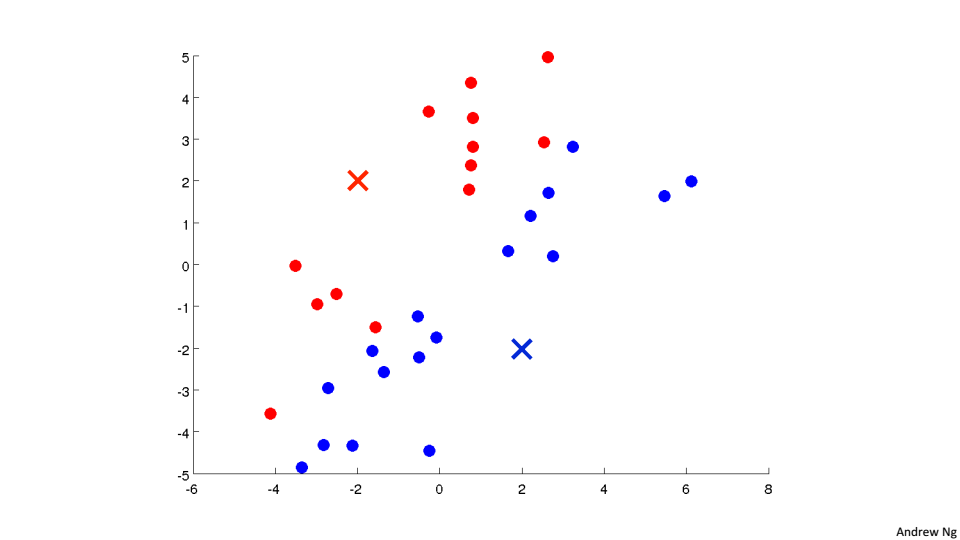
3、然後將紅色的聚類中心移動到所有紅色點的均值位置,藍色的聚類中心移動到所有藍色點的均值位置
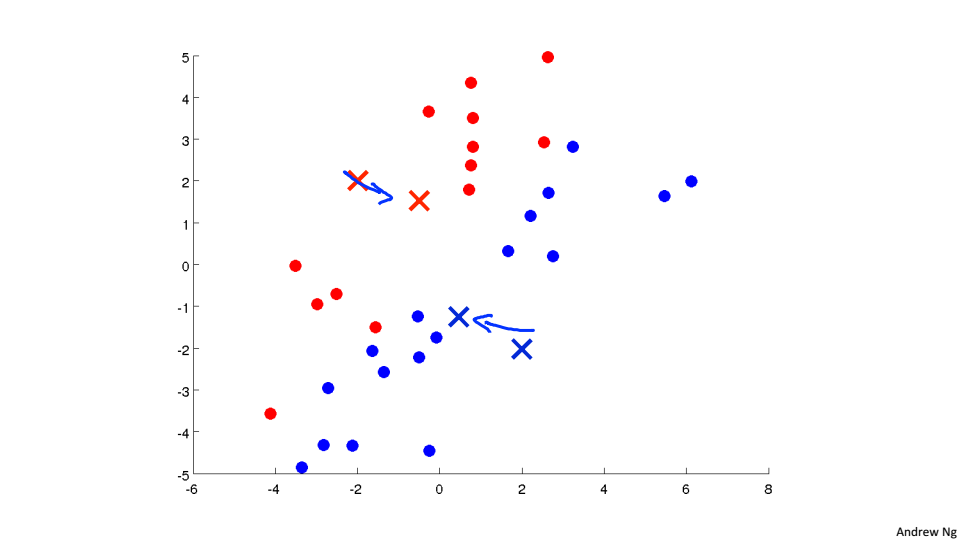
重複2、3過程直到收斂
K-Mean中的K就只的是要分為幾類

Opetimization objective
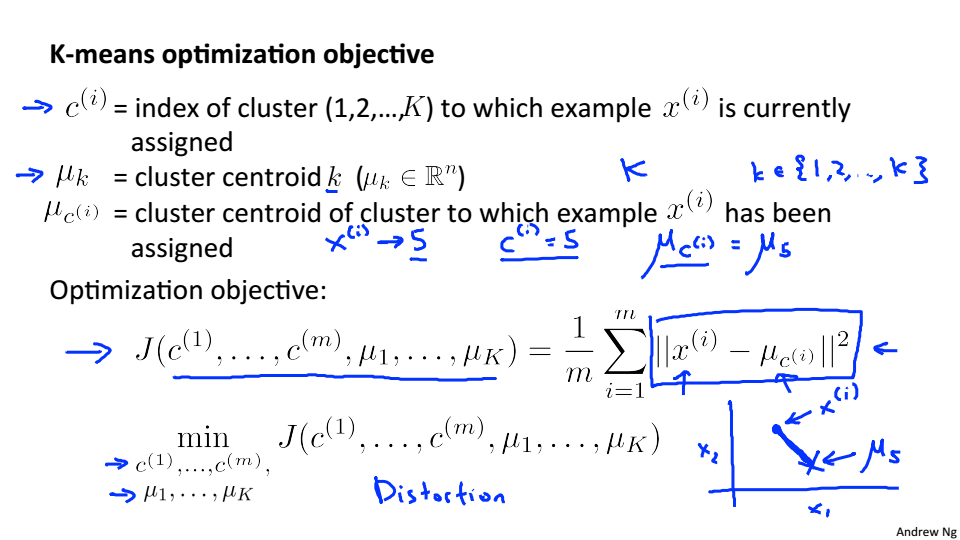
K-Mean中的優化目標
J是點到聚類中心的平均距離,J也被稱為失真函式
Random Initialization
隨機選取聚類中心
一般是隨機選取K個樣本,在讓聚類中心等於這些樣本

區域性最優
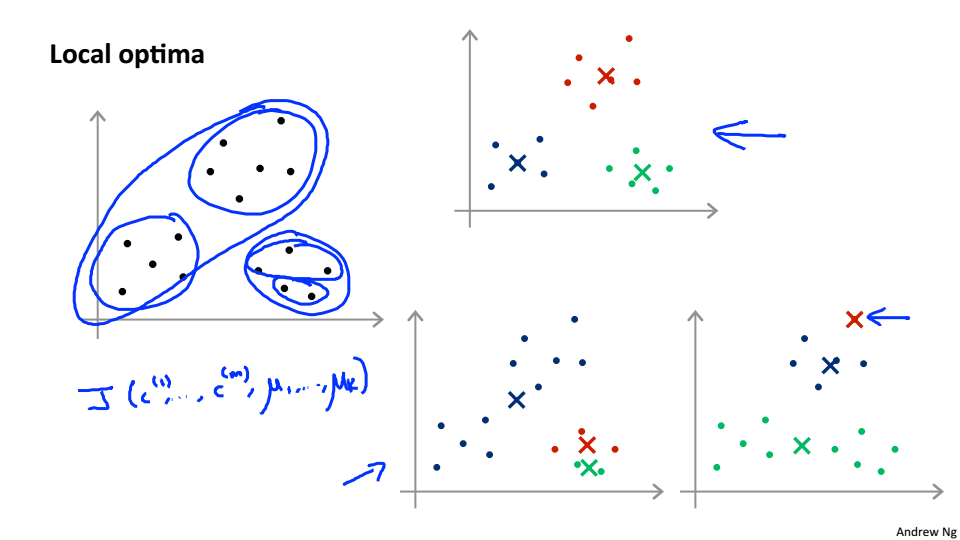
加入隨機初始化和代價函式後的K-Mean,最後的J的結果一般在2~10之間才是全域性最優解

Choosing the number of Clusters
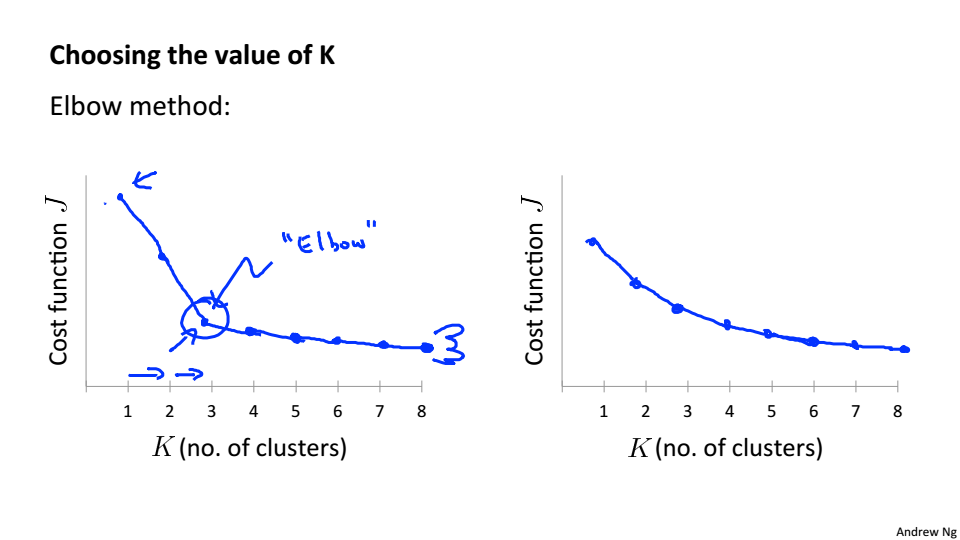
Elbow Method
繪製代價函式關於K的函式曲線,J會隨著K的增大而減小,逐漸趨於平穩,拐點處的K即我們所需要的K
但大部分情況拐點不是很清晰,不能很明顯的找出來
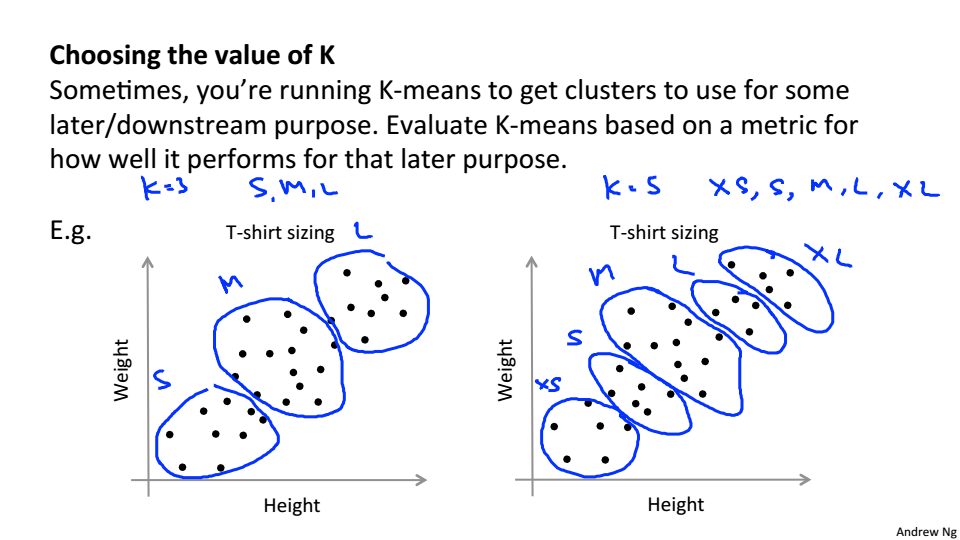
通過聚類要達到的目的來確定K的值,以T恤為例,如果T恤的尺碼只有S、M、L那麼K就應該選擇3
Motivation
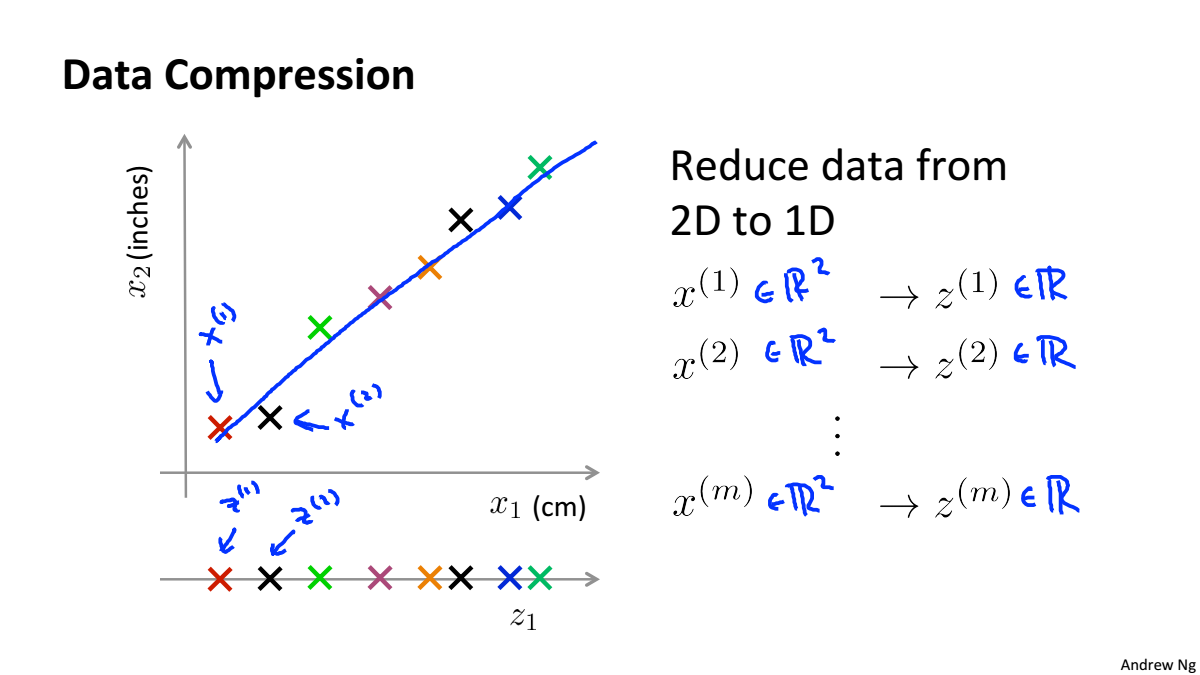
Data Compression
資料壓縮不僅可以使資料量減少,減小記憶體和硬碟的佔用,而且可以提高演算法的計算速度
資料壓縮就是尋找相關特徵之間的關係如下圖中的x1和x2都是表示長度,只是單位不一樣,就可以根據他們的線性關係,合併為一個一維特徵
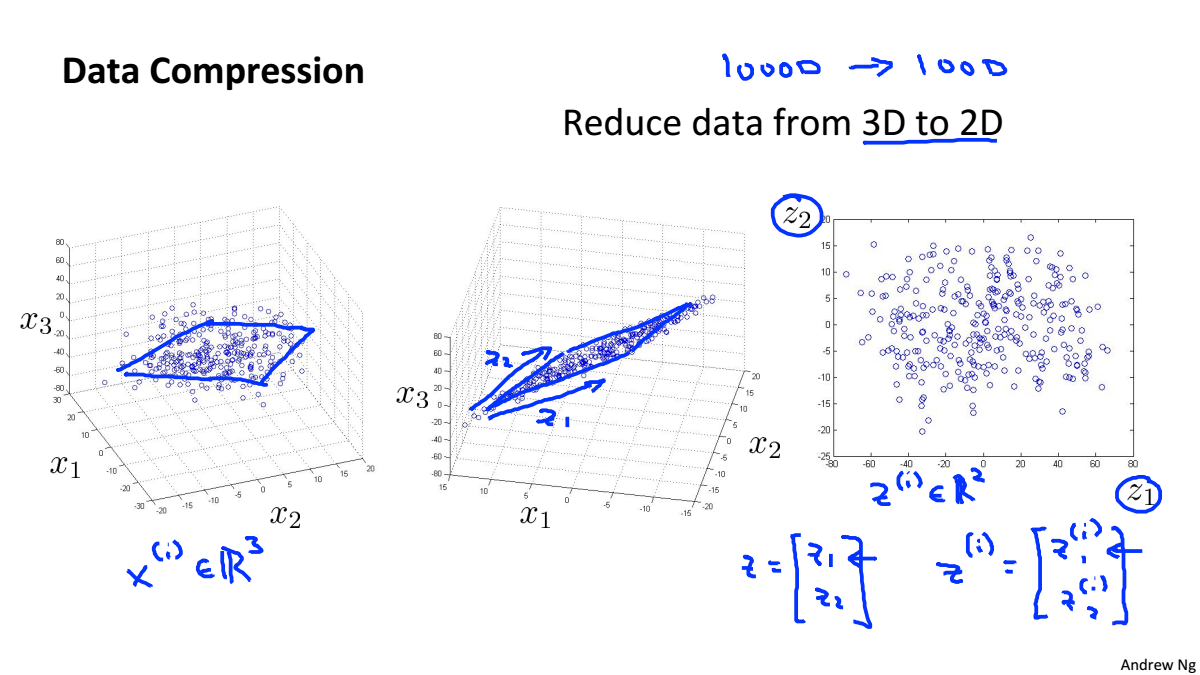
三維資料降到二維
將三維資料投影到一個二維平面
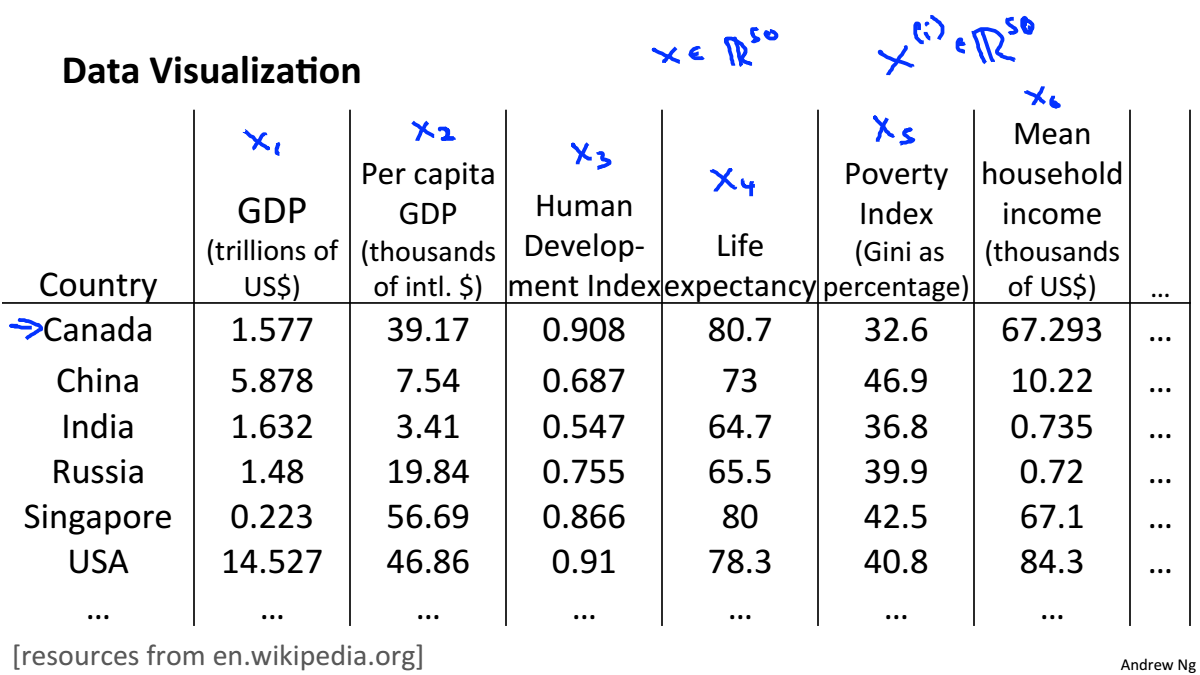
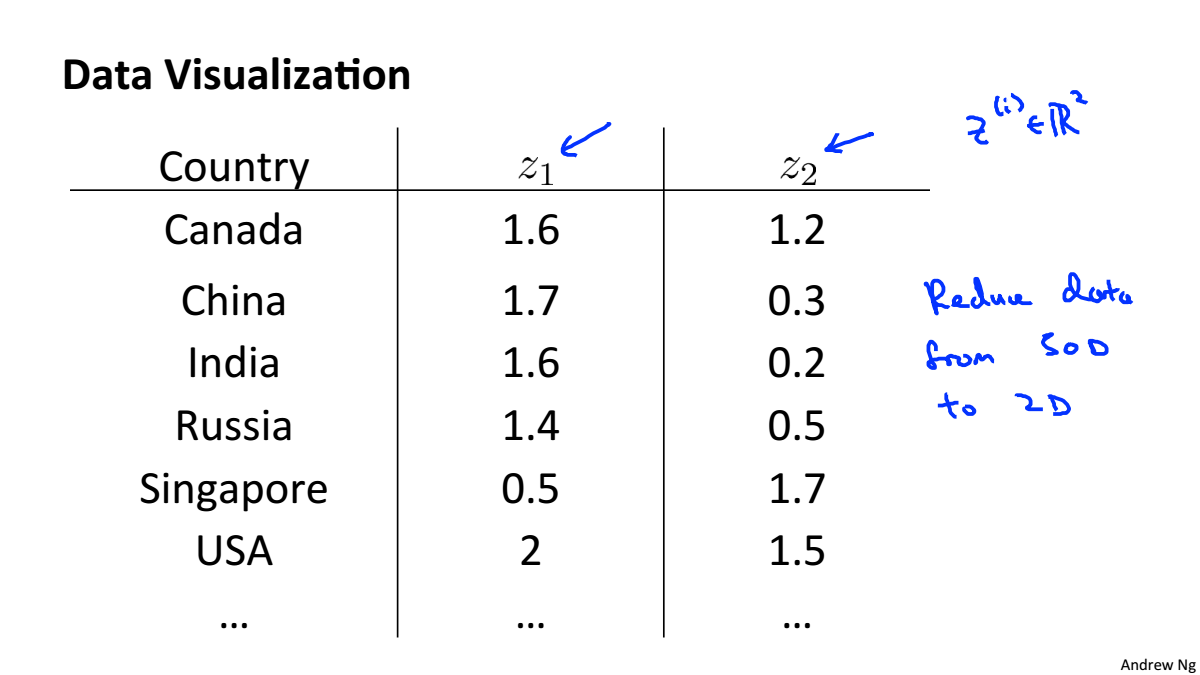
Data Visualiztion
一個高維資料可以被計算機處理,但人只能感知三維的資料,所以在做高維資料視覺化時,要先對資料進行降維,在進行視覺化。
Principal Component Analysis
Principal Component Analysis Problem Formulation
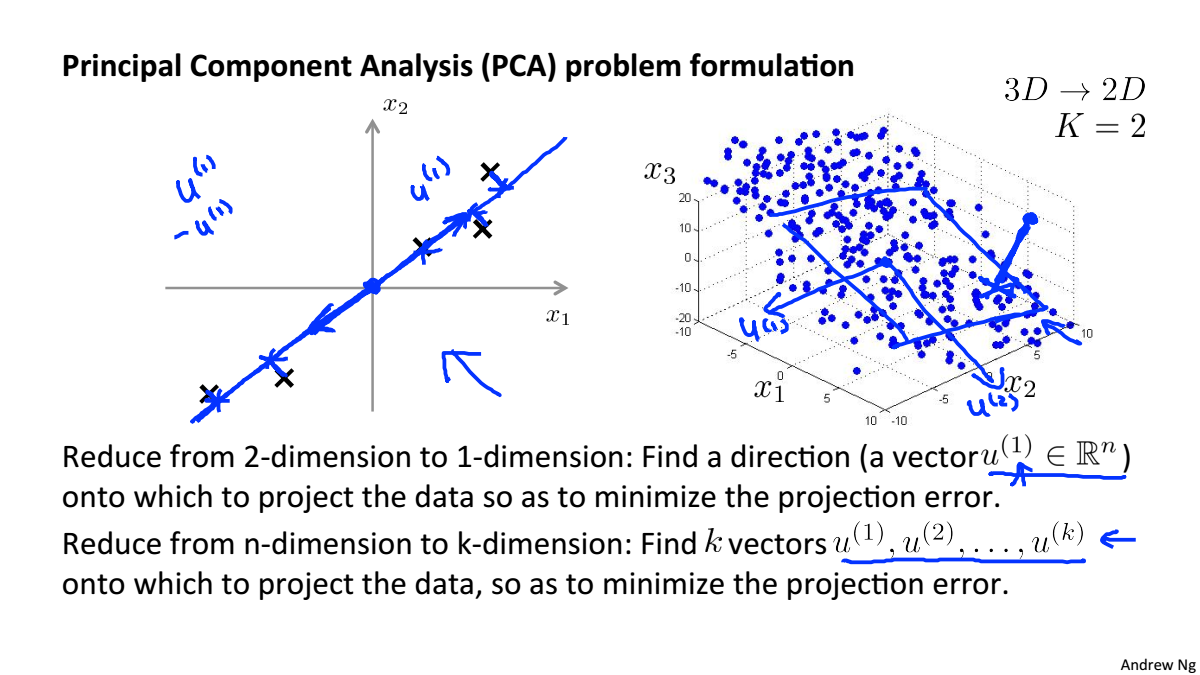
PCA將高維資料投影到低維空間,使得資料投影到這個面的誤差最小,這個誤差也叫作投影誤差,在進行降維之前,要對資料進行均值歸一化和特徵規範化
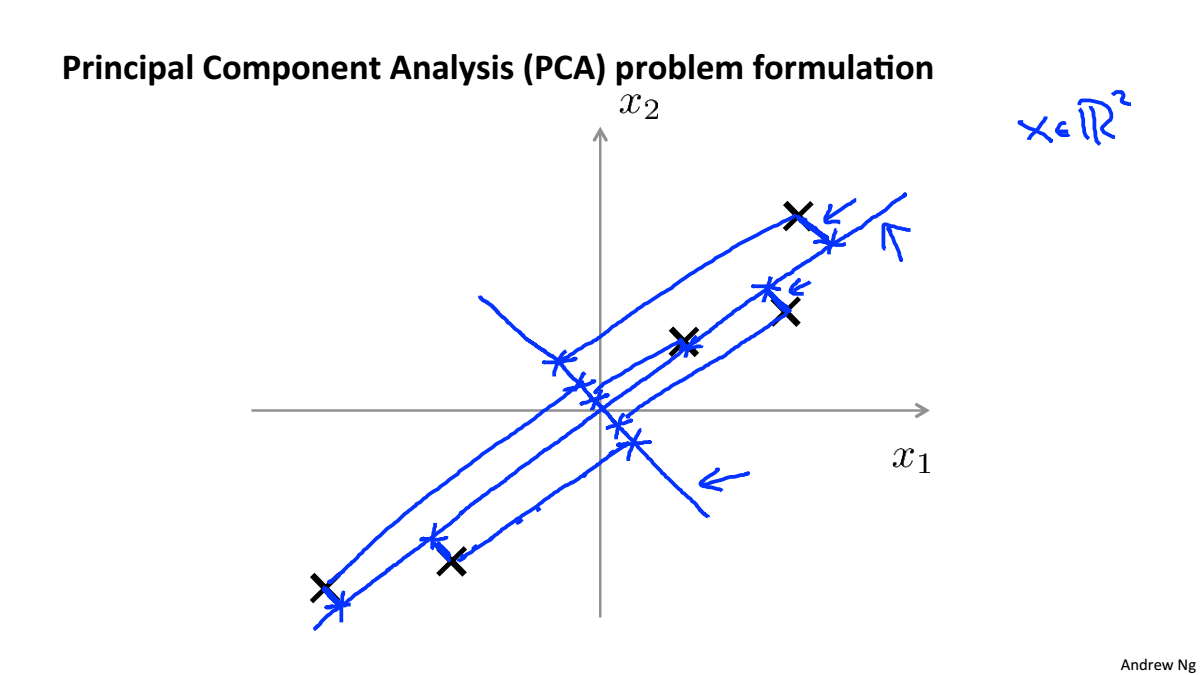
對於二維降到一維,是要尋找一個向量,使得投影誤差最小
對於n維降到k維,是要尋找k個向量,使得投影誤差最小
PCA和線性迴歸的區別:
- 線性迴歸的誤差是結果值得誤差,PCA是點到投影面的距離
- PCA是無監督學習
Principal Component Analysis Algorithm
資料預處理(特徵縮放/均值歸一化)

PCA演算法的步驟:
- 計算協方差矩陣
- 使用svd計算
的特徵值和特徵向量

- 將特徵向量按對應特徵值大小從上到下按行排列成矩陣,取前k行組成矩陣
-
就是降維之後的資料
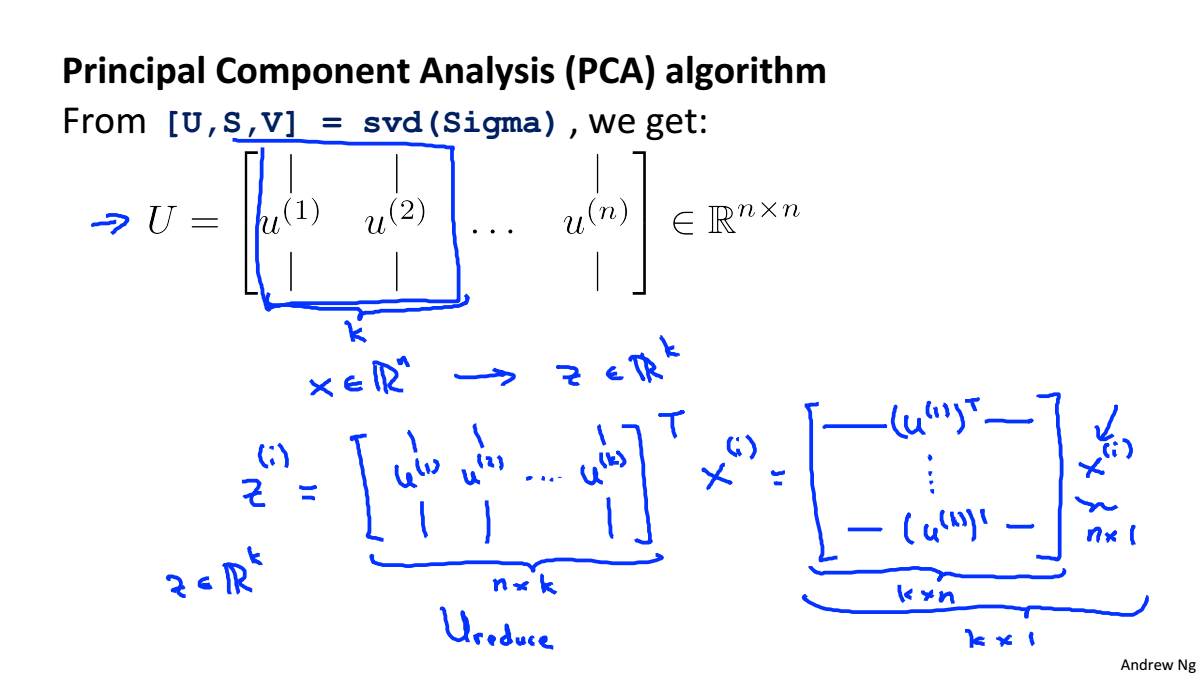
Applying PCA
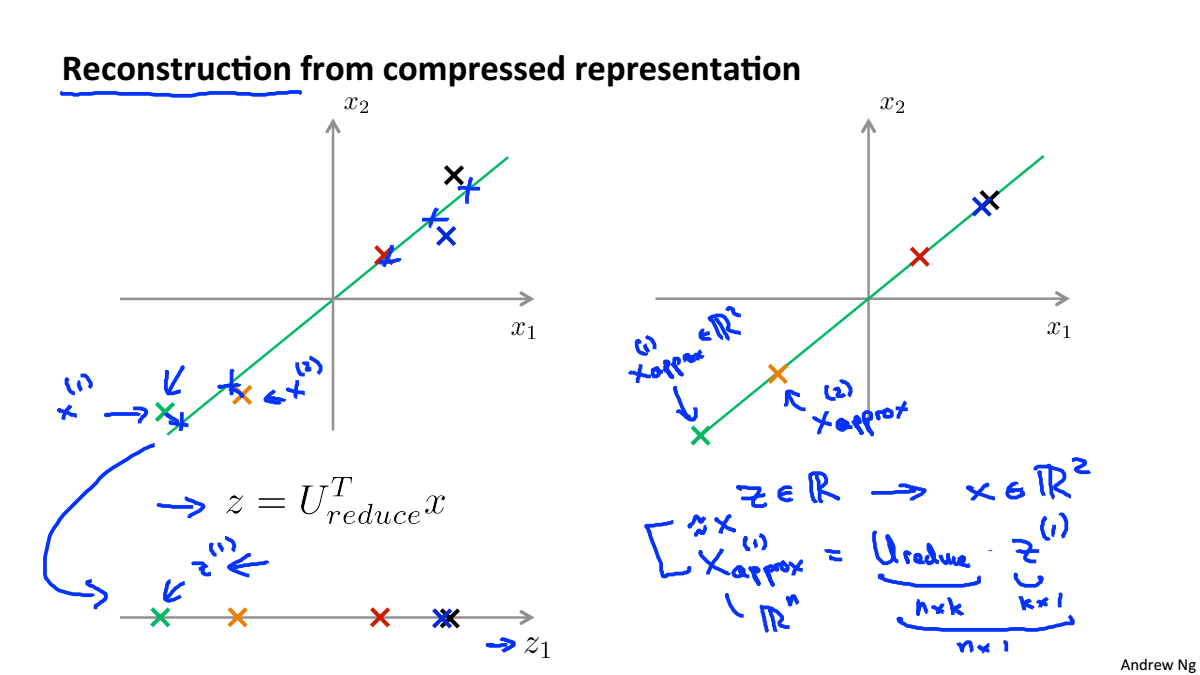
Reconstruction from Compressed Representation
Choosing the Number of Principal Components
計算平均投影誤差和總變差的比,選擇該值最小時候的K,該值表示的是與原資料的差異性,當為0.01時代表PCA保留了99%的差異性

選擇K的兩種兩種方法:
- 嘗試不同的K,計算差異性,如果>99%則符合要求
- 根據svd的到奇異值矩陣,矩陣對角上前K個數的和除以全部數的和就是差異性,從而根據差異性找到K

Advice for applying PCA
監督學習加速
降維矩陣應該在訓練集上執行PCA獲得,得到降維矩陣後就可以在交叉驗證集合測試集上使用

PCA並不是一個防止過擬合的好方法,應當使用正則化來防止過擬合

