三元環是一個不怎麼常見的黑科技，它的求解方法是一種基於分塊思想的方法，比較簡單好寫，在這裡介紹一下三元環的計數方法及正確性與時間複雜度證明。

對於一個n個點m條邊的無向圖，三元環是指對於圖上的三個點，兩兩點之間都直接有邊相連，這三個點組成的環就是三元環。

三元環的計數方法：記錄圖中每個點的度數，對於每條邊將它定向。對於一條邊，將度數大的點指向度數小的點，如果度數相同就將編號小的點指向編號大的點。計數時列舉每個點，對於每個點x列舉它的出邊，並將出邊指向的點y打標記，對於所有出邊指向的點y再枚舉出邊，如果這個出邊指向的點z被打了標記，那麼x,y,z就組成了一個三元環。時間複雜度為O(m√m)。

對於這個方法只需要證明三點：

1、將邊定向後的圖是有向無環圖(DAG)

這個很好證明，因為按照上述定向規則，我們稱x連向y表示x比y大，那麼任意兩個點的大小關係是固定的，每個點只會向比它小的點連邊，所以一定構成了有向無環圖。

2、每個三元環只會被統計一次

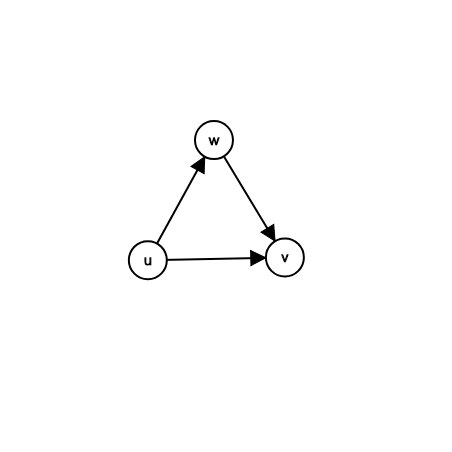
如圖所示，因為三元環上的邊是定向的，而且每個點只會枚舉出邊，所以每個三元環被統計的情況是唯一的。

3、時間複雜度為O(m√m)

考慮時間複雜度分為兩部分：一部分為每個點枚舉出邊，另一部分為每個出邊指向的點枚舉出邊。

第一部分時間複雜度顯然為O(n+m)，而第二部分我們分類討論：

如果一個點的出度大於√m，指向它的點出度一定要比它大，這樣的點最多√m個，時間複雜度為O(m√m)

如果一個點的出度小於√m，指向他的點最多有n個，時間複雜度為O(n√m)

綜上所述，時間複雜度為O(m√m)

三元環的題只找到了三道：

BZOJ3498

BZOJ5407

BZOJ5206