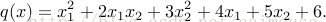在機器學習課程裡提到了這個矩陣，那麼這個矩陣是從哪裡來，又是用來作什麼用呢?先來看一下定義：

黑塞矩陣（Hessian Matrix），又譯作海森矩陣、海瑟矩陣、海塞矩陣等，是一個多元函式的二階偏導數構成的方陣，描述了函式的局部曲率。黑塞矩陣最早於19世紀由德國數學家Ludwig Otto Hesse提出，並以其名字命名。黑塞矩陣常用於牛頓法解決優化問題。

一般來說, 牛頓法主要應用在兩個方面, 1, 求方程的根; 2, 最優化.

在機器學習裡，可以考慮採用它來計算n值比較少的資料，在影象處理裡，可以抽取影象特徵，在金融裡可以用來作量化分析。

影象處理可以看這個連線：

量化分析可以看這個：

下面使用TensorFlow並且使用黑塞矩陣來求解下面的方程：

程式碼如下：

#python 3.5.3  蔡軍生    #http://edu.csdn.net/course/detail/2592    #  import tensorflow as tfimport numpy as npdef cons(x):    return tf.constant(x, dtype=tf.float32)def compute_hessian(fn, vars):    mat = []    for v1 in vars:        temp = []        for v2 in vars:            # computing derivative twice, first w.r.t v2 and then w.r.t v1
 
            temp.append(tf.gradients(tf.gradients(f, v2)[0], v1)[0])        temp = [cons(0) if t == None else t for t in temp] # tensorflow returns None when there is no gradient, so we replace None with 0        temp = tf.stack(temp)        mat.append(temp)    mat = tf.stack(mat)    return matx = tf.Variable(np.random.random_sample(), dtype=tf.float32)y = tf.Variable(np.random.random_sample(), dtype=tf.float32)f = tf.pow(x, cons(2
 
)) + cons(2) * x * y + cons(3) * tf.pow(y, cons(2)) + cons(4)* x + cons(5) * y + cons(6)# arg1: our defined function, arg2: list of tf variables associated with the functionhessian = compute_hessian(f, [x, y])sess = tf.Session()sess.run(tf.global_variables_initializer())print(sess.run(hessian))

再來舉多一個例子的原始碼，它就是用來計算量化分析，這個程式碼很值錢啊，如下：

#python 3.5.3  蔡軍生    #http://edu.csdn.net/course/detail/2592    # import numpy as npimport scipy.stats as statsimport scipy.optimize as opt#構造Hessian矩陣def rosen_hess(x):    x = np.asarray(x)    H = np.diag(-400*x[:-1],1) - np.diag(400*x[:-1],-1)    diagonal = np.zeros_like(x)    diagonal[0] = 1200*x[0]**2-400*x[1]+2    diagonal[-1] = 200    diagonal[1:-1] = 202 + 1200*x[1:-1]**2 - 400*x[2:]    H = H + np.diag(diagonal)    return Hdef rosen(x):    """The Rosenbrock function"""    return sum(100.0*(x[1:]-x[:-1]**2.0)**2.0 + (1-x[:-1])**2.0)def rosen_der(x):    xm = x[1:-1]    xm_m1 = x[:-2]    xm_p1 = x[2:]    der = np.zeros_like(x)    der[1:-1] = 200*(xm-xm_m1**2) - 400*(xm_p1 - xm**2)*xm - 2*(1-xm)    der[0] = -400*x[0]*(x[1]-x[0]**2) - 2*(1-x[0])    der[-1] = 200*(x[-1]-x[-2]**2)    return derx_0 = np.array([0.5, 1.6, 1.1, 0.8, 1.2])res = opt.minimize(rosen, x_0, method='Newton-CG', jac=rosen_der, hess=rosen_hess,                   options={'xtol': 1e-8, 'disp': True})print("Result of minimizing Rosenbrock function via Newton-Conjugate-Gradient algorithm (Hessian):")print(res)

====================== RESTART: D:/AI/sample/tf_1.43.py ======================Optimization terminated successfully.         Current function value: 0.000000         Iterations: 20         Function evaluations: 22         Gradient evaluations: 41         Hessian evaluations: 20Result of minimizing Rosenbrock function via Newton-Conjugate-Gradient algorithm (Hessian):     fun: 1.47606641102778e-19     jac: array([ -3.62847530e-11,   2.68148992e-09,   1.16637362e-08,         4.81693414e-08,  -2.76999090e-08]) message: 'Optimization terminated successfully.'    nfev: 22    nhev: 20     nit: 20    njev: 41  status: 0 success: True       x: array([ 1.,  1.,  1.,  1.,  1.])>>> 

可見hessian矩陣可以使用在很多地方了吧。

1. C++標準模板庫從入門到精通 

2.跟老菜鳥學C++

3. 跟老菜鳥學python

4. 在VC2015裡學會使用tinyxml庫

5. 在Windows下SVN的版本管理與實戰 

7.在VC2015裡使用protobuf協議

8.在VC2015裡學會使用MySQL資料庫

可以看更多的網站：

http://blog.csdn.net/ubunfans/article/details/41520047

http://blog.csdn.net/baimafujinji/article/details/51167852

http://jacoxu.com/jacobian%E7%9F%A9%E9%98%B5%E5%92%8Chessian%E7%9F%A9%E9%98%B5/

http://www.cnblogs.com/logosxxw/p/4651413.html