貝爾曼-福特(Bellman-Ford)演算法——解決負權邊(C++實現)
Dijkstra演算法雖然好,但是它不能解決帶有負權邊(邊的權值為負數)的圖。
接下來學習一種無論在思想上還是在程式碼實現上都可以稱為完美的最短路徑演算法:Bellman-Ford演算法。
Bellman-Ford演算法非常簡單,核心程式碼四行,可以完美的解決帶有負權邊的圖。
for(k=1;k<=n-1;k++) //外迴圈迴圈n-1次,n為頂點個數 for(i=1;i<=m;i++)//內迴圈迴圈m次,m為邊的個數,即列舉每一條邊 if(dis[v[i]]>dis[u[i]]+w[i])//嘗試對每一條邊進行鬆弛,與Dijkstra演算法相同 dis[v[i]]=dis[u[i]]+w[i];
在一個含有n個頂點的圖中,任意兩點之間的最短路徑最多包含n-1條邊,最短路徑中不可能包含迴路。
因為最短路徑是一個不包含迴路的簡單路徑,迴路分為正權迴路(迴路權值之和為正)和負權迴路(迴路權值之和為負)。如果最短路徑中包含正權迴路,那麼去掉這個迴路,一定可以得到更短的路徑;如果最短路徑中包含負權迴路,那麼肯定沒有最短路徑,因為每多走一次負權迴路就可以得到更短的路徑. 因此最短路徑肯定是一個不包含迴路的最短路徑,即最多包含n-1條邊。
Bellman-Ford演算法的主要思想:
首先dis陣列初始化頂點u到其餘各個頂點的距離為∞,dis[u] = 0。
然後每輪對輸入的所有邊進行鬆弛,更新dis陣列,至多需要進行n-1次就可以求出頂點u到其餘各頂點的最短路徑(因為任意兩點之間的最短路徑最多包含n-1條邊,所以只需要n-1輪就行)。
一句話概括Bellman-Ford演算法就是:對所有邊進行n-1次“鬆弛”操作。
此外,Bellman-Ford演算法可以檢測一個圖是否有負權迴路。如果已經進行了n-1輪鬆弛之後,仍然存在
if(dis[v[i]]>dis[u[i]]+w[i])
dis[v[i]]=dis[u[i]]+w[i];
的情況,也就是說在進行n-1輪之後,仍然可以繼續成功鬆弛,那麼這個圖一定存在負權迴路。
關鍵程式碼如下:
//Bellman-Ford演算法核心語句 for(k=1;k<=n-1;k++) //外迴圈迴圈n-1次,n為頂點個數 for(i=1;i<=m;i++)//內迴圈迴圈m次,m為邊的個數,即列舉每一條邊 if(dis[v[i]]>dis[u[i]]+w[i])//嘗試對每一條邊進行鬆弛,與Dijkstra演算法相同 dis[v[i]]=dis[u[i]]+w[i]; //檢測負權迴路 flag=0; for(i=1;i<=m;i++) if(dis[v[i]]>dis[u[i]]+w[i]) flag=1; if(flag==1) printf("此圖有負權迴路");
顯然,演算法複雜度為O(NM),比Dijkstra演算法還高,當然可以進行優化。
在實際操作中,Bellman-Ford演算法經常會在沒有達到n-1輪鬆弛前就已經計算出最短路,上面已經說過,n-1其實是最大輪迴次數。
因此可以新增一個變數check用來標記陣列dis在本輪鬆弛中是否發生了變化,若沒有變化,則提前跳出迴圈。
程式碼:
#include <iostream>
#define INF 1e9
void DFSPrint(int bak[], int k)
{
if (bak[k] == k)
{
printf("%d ", k);
return;
}
DFSPrint(bak, bak[k]);
printf("%d ", k);
return;
}
int main()
{
int i, j, n, m;
int dis[10], bak[10], u[10], v[10], w[10];
int check;
// 讀入n和m, n表示頂點個數,m表示邊的條數
scanf("%d %d", &n, &m);
// 讀入邊
for (i = 1; i <= m; ++i)
{
scanf("%d %d %d", &u[i], &v[i], &w[i]);
}
// 初始化bak[]陣列,前驅結點均為自己
// 初始化dis[]陣列,源點為1號頂點
for (i = 1; i <= n; ++i)
{
bak[i] = i;
dis[i] = INF;
}
dis[1] = 0;
// Bellman-Ford演算法
for (j = 1; j <= n-1; ++j) // 最多迴圈n-1輪(圖退化為連結串列)
{
check = 0; // 用來標記在本輪鬆弛中陣列dis是否發生更新
for (i = 1; i <= m; ++i)
{
if (dis[u[i]] != INF && dis[u[i]] + w[i] < dis[v[i]]) // relax
{
dis[v[i]] = dis[u[i]] + w[i];
bak[v[i]] = u[i];
check = 1;
}
}
if (check == 0)
{
break;
}
}
// 檢測負權迴路,若存在,則在對邊進行一次遍歷後必定會有relax的操作
int flag = 0;
for (i = 1; i <= m; ++i)
{
if (dis[u[i]] + w[i] < dis[v[i]])
{
flag = 1;
}
}
if (flag)
{
printf("該圖有負權迴路");
}
else
{
// 輸出最終結果
printf("最終結果為:\n");
for (i = 1; i <= n; ++i)
{
printf("1號頂點到%d號頂點的最短距離為:%d\n", i, dis[i]);
}
printf("\n列印1號頂點到5號頂點的最短路徑:\n");
DFSPrint(bak, 5);
}
return 0;
}
示意圖1:
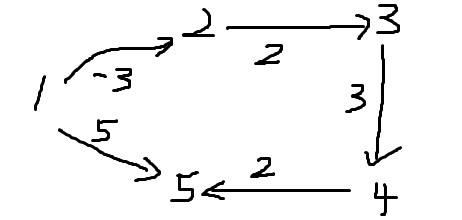
執行結果1:
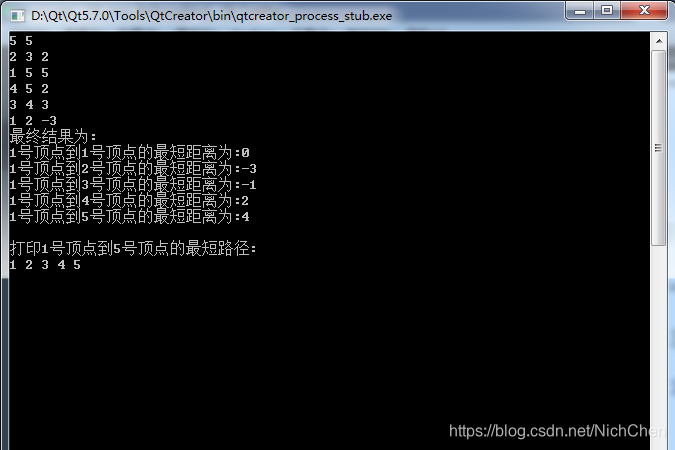
示意圖2:
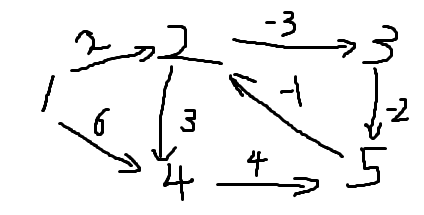
執行結果2:

參考部落格:https://blog.csdn.net/fengyuzhiren/article/details/59030523
