基於MapReduce的大矩陣乘法(Spark實現)
阿新 • • 發佈:2018-12-20
矩陣-向量乘法實現
xi=∑j=1nmijvj
Map函式
Map函式應用於M的一個元素,但是如果執行Map任務的計算節點還沒有將v讀到記憶體,那麼首先以一個整體的方式讀入v,然後v就可以被該Map任務中執行的Map函式所用。每個Map任務將整個向量v和矩陣M的一個檔案塊作為輸入。對每個矩陣元素mij
,Map任務會產生鍵值對(i,mijvj)。因此,計算xi的所有n個求和項mijvj
。
Reduce函式
Reduce函式簡單地將所有與給定鍵i關聯的值相加即得到結果(i,xi)
。
向量v太大無法放入記憶體
把矩陣分割成多個寬度相等的垂直條,同時將向量分割成同樣數目的水平條。我們的目標是使用足夠的條以保證向量的每個條能夠方便地放入計算節點的記憶體中。
矩陣-矩陣乘法
矩陣M
中第i行第j列的元素記為mij,矩陣N中第j行第k列的元素記為njk,矩陣P=MN,其第i行第k列的元素記為pik
,
pik=∑jmijnjk
Map函式
對每個矩陣元素mij
產生鍵值對(j,(M,i,mij)),對每個矩陣元素njk產生鍵值對(j,(N,k,njk))
。
Reduce函式
對每個鍵j
,對每個(M,i,mij)和(N,k,njk),產生鍵值對,其中鍵為(i,k),值為mijnjk
。
Reduce函式
對每個鍵(i,k)
,計算與此鍵相關聯的所有值的和,記為((i,k),v)
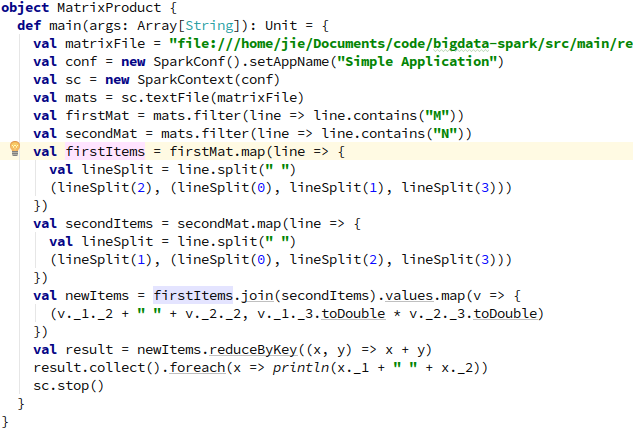
以下是使用Spark來實現上面矩陣與矩陣相乘的演算法,輸入是一份檔案,檔案的每一行為矩陣名 行號 列號 值