關於softmax、argmax、softargmax 關於softmax、argmax、softargmax
關於softmax、argmax、softargmax
在閱讀LIFT:Learned Invariant Feature Transform一文時,文中第1節提到為了保證端到端的可微性,利用softargmax來代替傳統的NMS(非極大值抑制)來挑選極值點位置。由於只瞭解softmax,對於softargmax不甚瞭解,所以記錄下來。
1)softmax:
輸入為向量,輸出為值為0-1之間的向量,和為1。在分類任務中作為概率出現在交叉熵損失函式中。
import numpy as np data=np.array([0.1, 0.3, 0.6, 2.1 ,0.55]) np.exp(data)/np.sum(np.exp(data)) # softmax
array([ 0.07795756, 0.09521758, 0.12853029, 0.57603278, 0.12226179])
2)argmax:為了得到一個向量中最大值所處的位置,我們利用此函式。但是這個函式不可導,所以無法計算其梯度。然而我們可以利用軟化的max函式來計算,就是softmax。利用softmax,我們可以得到每個元素正則化後的值。此向量()分佈)的
此時最大值所處的座標期望即為:![]()
np.sum(np.exp(data)/np.sum(np.exp(data)) * np.array([0,1,2,3,4])) # E = p*index
2.5694236670240085。而最大之所在的位置應該是3。
3)softargmax:從上面看到位置計算不夠準確,一個原因就是最大值的概率不夠大,或者說增大相對最大值而減弱其他值的影響就可以得到更加準確的位置座標。
softargmax: 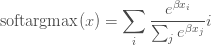
可以看到,上式與softmax的期望只有一個差別,即給向量的每個元素乘以beta。
>>>d = data*10 # beta=10 array([ 1. , 3. , 6. , 21. , 5.5]) >>> np.sum(np.exp(d)/np.sum(np.exp(d)) *np.array([0,1,2,3,4])) 2.9999998429934758
可見此時輸出的座標為2.99,即為3,且這種尋找極值所在位置(座標)的方法是可微的。常用於影象特徵點位置的提取。
此外,LIFT原文3.5節提到:softargmax作為非極大值抑制NMS的可微分版本。就是說可以利用softargmax來替代NMS。
Ref:
IFT6266 PROJECT
在閱讀LIFT:Learned Invariant Feature Transform一文時,文中第1節提到為了保證端到端的可微性,利用softargmax來代替傳統的NMS(非極大值抑制)來挑選極值點位置。由於只瞭解softmax,對於softargmax不甚瞭解,所以記錄下來。
1)softmax:
輸入為向量,輸出為值為0-1之間的向量,和為1。在分類任務中作為概率出現在交叉熵損失函式中。
import numpy as np data=np.array([0.1, 0.3, 0.6, 2.1 ,0.55]) np.exp(data)/np.sum(np.exp(data)) # softmax
array([ 0.07795756, 0.09521758, 0.12853029, 0.57603278, 0.12226179])
2)argmax:為了得到一個向量中最大值所處的位置,我們利用此函式。但是這個函式不可導,所以無法計算其梯度。然而我們可以利用軟化的max函式來計算,就是softmax。利用softmax,我們可以得到每個元素正則化後的值。此向量()分佈)的
此時最大值所處的座標期望即為:![]()
np.sum(np.exp(data)/np.sum(np.exp(data)) * np.array([0,1,2,3,4])) # E = p*index
2.5694236670240085。而最大之所在的位置應該是3。
3)softargmax:從上面看到位置計算不夠準確,一個原因就是最大值的概率不夠大,或者說增大相對最大值而減弱其他值的影響就可以得到更加準確的位置座標。
softargmax: 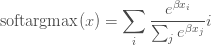
可以看到,上式與softmax的期望只有一個差別,即給向量的每個元素乘以beta。
>>>d = data*10 # beta=10 array([ 1. , 3. , 6. , 21. , 5.5]) >>> np.sum(np.exp(d)/np.sum(np.exp(d)) *np.array([0,1,2,3,4])) 2.9999998429934758
可見此時輸出的座標為2.99,即為3,且這種尋找極值所在位置(座標)的方法是可微的。常用於影象特徵點位置的提取。
此外,LIFT原文3.5節提到:softargmax作為非極大值抑制NMS的可微分版本。就是說可以利用softargmax來替代NMS。
Ref:
