資料結構學習筆記--BST與AVL
資料結構學習筆記–BST與AVL
前言
BST和AVL複習。
BST
二叉排序樹的3個主要性質:
- 若左子樹不空,則左子樹上的所有節點的值均小於根節點的值。
- 若右子樹不空,則右子樹上的所有節點的值均大於根節點的值。
- 左、右子樹也分別為二叉排序樹。
對於插入操作,按照上述規則,遞迴即可。 但是對於刪除操作,涉及到排序規則的保持,可分3中情況考慮:
- 若刪除節點為葉子節點,則刪除該節點不影響整棵樹的結果,只需修改父節點指標即可。
- 若刪除節點只有左子樹或只有右子樹,此時,只要令左子樹或右子樹替換刪除節點即可。
- 若左子樹與右子樹均不為空,則使用刪除節點的直接後繼節點的值代替刪除節點的值,然後刪除直接後繼節點即可。
嚴蔚敏版的資料結構,對於第3中情況,有不同兩種處理方式:
- 使刪除節點的左子樹代替刪除節點,使刪除節點的右子樹成為刪除節點直接前驅的右子樹。 或
- 使用刪除節點的直接前驅的值代替刪除節點的值,然後刪除直接前驅節點。
其中第2種方式與上面第3中情況的處理方式類似,容易理解,因為要保持順序性,要麼直接前驅、要麼直接後繼來代替,才能保持有序; 第1種方式稍微有點繞,不過刪除節點右子樹成為直接前驅的右子樹,也是保持著有序性的。
不過從程式碼實現的簡潔程度和便於理解的角度,我傾向於使用上面第3種情況的處理方式。
AVL
BST在插入關鍵字有序時,會蛻化為單支樹,所以引出了平衡二叉樹。平衡二叉樹除了具有二叉搜尋樹的性質外,還有兩個性質:
- 左子樹和右子樹都是平衡二叉樹。
- 左子樹和右子樹高度只差的絕對值不超過1。
節點高度的定義為從該節點到葉子節點的路徑(邊)的長度,葉子節點的高度為0。
從多出來的兩個性質可以看出,變化主要在插入和刪除操作上,對於這兩個操作,除了要保持順序性,現在還要保持平衡。
 假設在節點v上出現了不平衡:
bf = height(v.left) - height(v.right)
bf2 = height(v.left.left) - height(v.left.right)
bf3 = height(v.right.left) - height(v.right.right)
假設在節點v上出現了不平衡:
bf = height(v.left) - height(v.right)
bf2 = height(v.left.left) - height(v.left.right)
bf3 = height(v.right.left) - height(v.right.right)
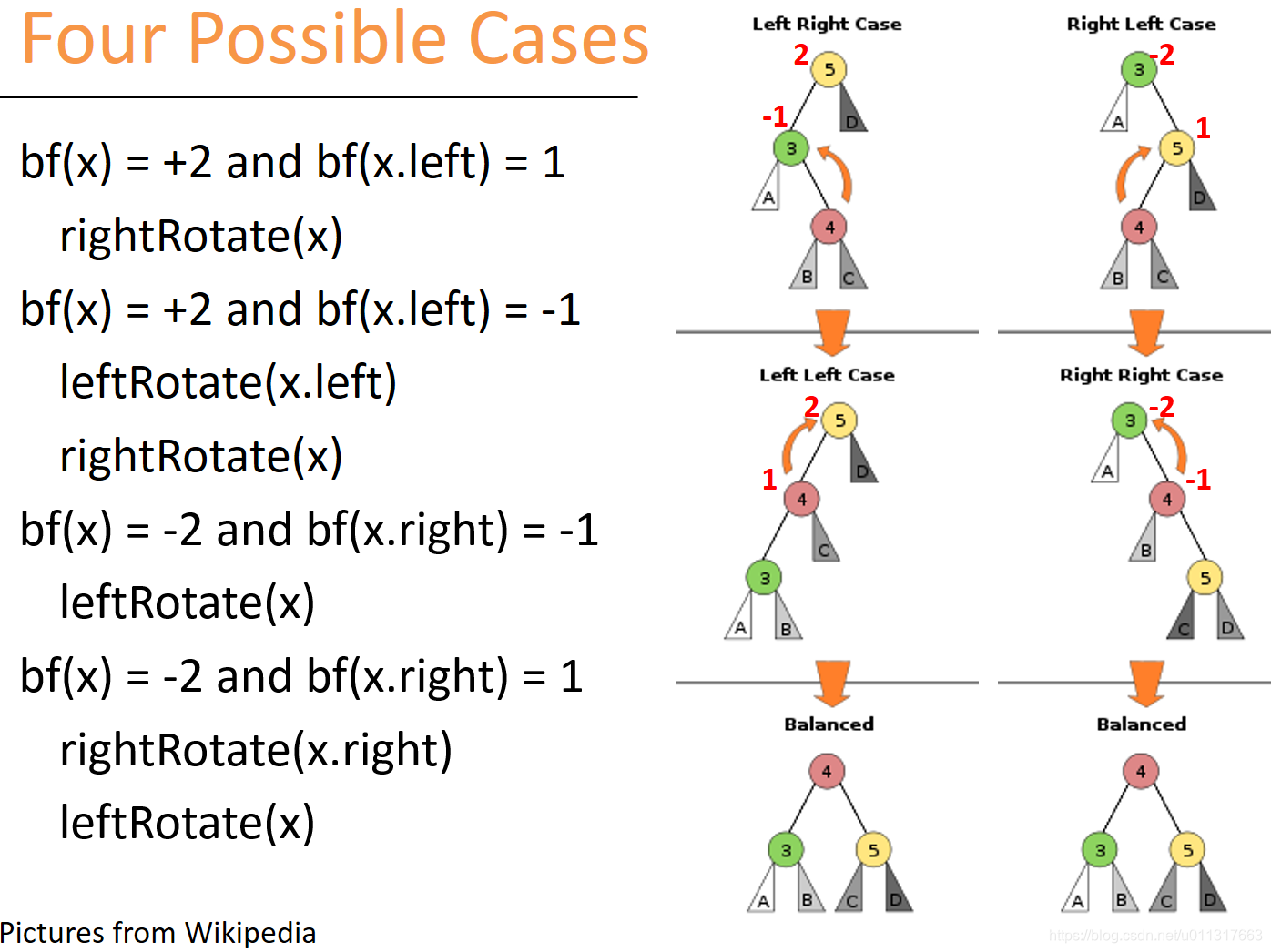
則有四種不平衡的場景:
- bf=2,bf2=1
- bf=2, bf2=-1
- bf=-2, bf3=1
- bf=-2, bf3=-1
場景梳理出來,就有對應的解決方法:
- 單向右旋。 (對應場景1。)
- 單向左旋。 (對應場景4。)
- 先右旋,後左旋。 (對應場景3)
- 先左旋,後右旋。 (對應場景2)
另一種方式是使用平衡因子,也就是上面算的bf來作為節點屬性進行平衡操作,具體參見嚴蔚敏版的資料結果。 不過,同樣,從程式碼實現和便於理解的角度來看,我傾向於使用高度來作為節點屬性。
總結
BST和AVL原理簡單清晰,但是真要自己動手實現起來,還是很麻煩的,尤其是想把程式碼寫的簡潔。 慣例吐槽,嚴蔚敏版的資料結構,讀起來確實累。
附錄:
附上自己的實現(JAVA版)
程式碼參考了VISUALGO的實現,沒有註釋,結合上面的描述對應著看吧。
/**
* avl tree
* @author lhz
*/
public class AvlTree extends BinarySearchTree {
public void insert(Comparable v) {
if (v == null) {
throw new NullPointerException();
}
root = insert(root, v);
}
private int height(Node v) {
return v == null ? -1 : v.height;
}
private Node rotateRight(Node v) {
Node lc = v.left;
v.left = lc.right;
if (lc.right != null) {
lc.right.parent = v;
}
lc.right = v;
lc.parent = v.parent;
v.parent = lc;
v.height = Math.max(height(v.left), height(v.right)) + 1;
lc.height = Math.max(height(lc.left), height(lc.right)) + 1;
return lc;
}
private Node rotateLeft(Node v) {
Node rc = v.right;
v.right = rc.left;
if (rc.left != null) {
rc.left.parent = v;
}
rc.parent = v.parent;
rc.left = v;
v.parent = rc;
v.height = Math.max(height(v.left), height(v.right)) + 1;
rc.height = Math.max(height(rc.left), height(rc.right)) + 1;
return rc;
}
@Override
protected Node insert(Node v, Comparable k) {
v = super.insert(v, k);
v = balance(v);
return v;
}
public void remove(Comparable v) {
root = remove(root, v);
}
@Override
protected Node remove(Node v, Comparable k) {
v = super.remove(v, k);
v = balance(v);
return v;
}
protected Node balance(Node k) {
if (k == null) {
return null;
}
int balance = height(k.left) - height(k.right);
if (balance == 2) {
int balance2 = height(k.left.left) - height(k.left.right);
if (balance2 == 1) {
k = rotateRight(k);
} else {
k.left = rotateLeft(k.left);
k = rotateRight(k);
}
} else if (balance == - 2) {
int balance2 = height(k.right.left) - height(k.right.right);
if (balance2 == -1) {
k = rotateLeft(k);
} else {
k.right = rotateRight(k.right);
k = rotateLeft(k);
}
}
k.height = Math.max(height(k.left), height(k.right)) + 1;
return k;
}
}
/**
* avl tree
* @author lhz
*/
public class BinarySearchTree {
class Node {
public Comparable value;
public int bf; //balance factor
public int height;
public int ref;//same value reference count
public Node left;
public Node right;
public Node parent;
public Node(Comparable v) {
value = v;
}
public String toString() {
return String.format("[%s:%d, h=%d, bf=%d]", value, ref, height, bf);
}
}
protected Node root;
public Comparable min(Node v) {
if (v == null) {
return null;
}
while (v.left != null) {
v = v.left;
}
return v.value;
}
public Comparable max(Node v) {
if (v == null) {
return null;
}
while (v.right != null) {
v = v.right;
}
return v.value;
}
public Node search(Node v, Comparable k) {
if (v == null) {
return null;
}
int compared = k.compareTo(v.value);
if (compared > 0) {
return search(v.right, k);
} else if (compared < 0) {
return search(v.left, k);
} else {
return v;
}
}
protected Node insert(Node v, Comparable k) {
if (v == null) {
return new Node(k);
}
int compared = k.compareTo(v.value);
if (compared > 0) {
v.right = insert(v.right, k);
v.right.parent = v;
} else if (compared < 0) {
v.left = insert(v.left, k);
v.left.parent = v;
} else {
v.ref++;
}
return v;
}
protected Node remove(Node v, Comparable k) {
if (v == null) {
return null;
}
int compared = k.compareTo(v.value);
if (compared > 0) {
v.right = remove(v.right, k);
if (v.right != null) v.right.parent = v;
} else if (compared < 0) {
v.left = remove(v.left, k);
if (v.left != null) v.left.parent = v;
} else {
if (v.right == null && v.left == null) {
return null;
} else if (v.left != null && v.right != null) {
Comparable s = successor(v);
v.value = s;
v.right = remove(v.right, s);
} else if (v.left != null) {
return v.left;
} else if (v.right != null) {
return v.right;
}
}
return v;
}
protected Comparable successor(Node v) {
if (v.right != null) {
return min(v.right);
} else {
Node p = v.parent;
Node c = v;
while (p != null && p.right == c) {
c = p;
p = p.parent;
}
return p == null ? null : p.value;
}
}
protected Comparable predecessor(Node v) {
if (v.left != null) {
return max(v.left);
} else {
Node p = v.parent;
Node c = v;
while (p != null && p.left == c) {
c = p;
p = p.parent;
}
return p == null ? null : p.value;
}
}
}
