傅立葉定律（熱傳導定律）

						q= -λ ∂T/∂t
			表示單位時間內通過單位面積的熱量的大小，溫度梯度的反方向

三類邊界條件：

• 第一類邊界條件：已知表面溫度
• 第二類邊界條件：已知邊界上的熱流變化規律，即溫度沿邊界法線方向的導數，稱為第二類邊界條件，表示式如下： q=-λ ∂T/∂t
• 第三類邊界條件：已知邊界氣流溫度及對流換熱係數 1、 非穩態熱傳導方程：左邊體現溫度隨時間變化，右邊體現了物體內部溫度傳導過程: ρc ∂T/∂t=(∂T^2)/(∂z^2 )

要求解一個實際的溫度場分佈需要：

溫度場分佈 = 熱傳導方程 + 單值性條件 單值性條件一般指三類邊界條件、初始條件等 求解方法：有限元法、數值解法、有限差分法 採用有限差分法差分後： T(p,k)=T(p,k-1)+ Δλ/ρc•(T(p-1,k-1)-2T(p,k-1)+T(p+1,k-1))/〖Δz〗^2 控制容積法劃分網格：利用中心點作為溫度節點的中心，節點位於子區域的中心.

外界點法：

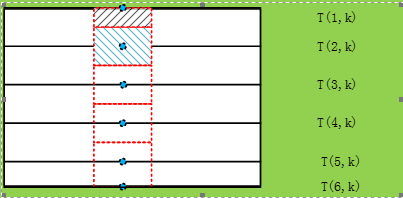
邊界節點匯入邊界方程：

1、補充邊界節點的方法： 第二類邊界條件： q=-λ ∂T/∂t

採用控制容積，外界點法時：  外設源項T(0,k) ，如下圖:

則有： q=-λ ∂T/∂t= -λ (T(2,k)-T(1,k))/Δz 截差為O(x) 則：T(1,k)=T(2,k)+(Δz•q)/λ 一般要內部節點和外部節點的截差要相同，顯示差分方程直接差分後的截差為O(x^{2)，故邊界節點處的差分後的截差也需為O(x}

2)，採用中心差分時截差為O(x^2)，則有： λ (T(0,k)-T(2,k))/2Δz=q T(0,k)= T(2,k)+2qΔz/λ 為消去T(0,k)，由一維，非穩態、不含內熱源的控制方程可得在T(1,k)處的離散形式： λ (T(2,k)-2T(1,k)+T(0,k))/(Δz^2 )=ρc (T(1,k+1)-T(1,k))/∆t 將上式T(0,k)帶入，有 λ (T(2,k)-2T(1,k)+T(2,k)+2qΔz/λ)/(Δz^2 )=ρc (T(1,k+1)-T(1,k))/∆t λ (T(2,k)-T(1,k))/(Δz^2 )+q=Δz/2 ρc (T(1,k+1)-T(1,k))/∆t

2、根據能量守恆：

根據邊界層的能量守恆，微元體熱能的增量=流入的能量-流出的能量 則根據能量守恆： ρc dT/dt S=- λ (T(p,k)-T(p-1,k))/∆z-(-λ (T(p+1,k)-T(p,k))/∆z) ρc dT/dt Δz/2•1•1=λ (T(p+1,k)-2T(p,k)+T(p-1,k))/∆z 則可以得到邊界層下一時刻溫度T(p,k+1)如下： ρc (T(p,k+1)-T(p,k))/∆t= λ (T(p+1,k)-2T(p,k)+T(p-1,k))/(Δz^2 ) T(1,k+1)=T(1,k)+Δt/ρcΔz q_u(k) + Δtλ/(ρcΔz^2 )•[T(2,k)-T(1,k)] 內部導熱對非穩態導熱方程差分後得到： T(p,k+1)=T(p,K)+ Δtλ/ρc•(T(p-1,k)-2T(p,k)+T(p+1,k))/〖Δz〗^2 對於顯式差分： q_u(k) = ∅(T(k)g^4- T(k)b^4) 求解方法迭代即可求解出物體內部溫度分佈情況 對於顯示差方程： q_u(k+1) = ∅(T(k+1)^4- T(k)^4) 採用追趕法求解各層溫度分佈