人臉識別

分類

1. Verification：一對一識別，給一張照片，看是否是給定的照片
2. Recognition：一對n識別，給一張照片看是否是資料庫中的人 顯然 Recognition可以通過n次Verification完成

One-shot learning

人臉識別需要解決的一個問題是one-shot learning，即通過一張照片或一個樣例就能識別這個人。一種方法是可以基於資料集搭建一個神經網路，輸入一張照片時判斷屬於哪個類別。這樣做的缺點是如果資料庫加入新人那麼需要重新訓練網路很不方便。於是提出了構建一個similarity function。d(img1, img2)即反映了img1和img2之間的相似度，基於該公式就可以將輸入圖片歸類於最相似的圖片。

Sigmese network

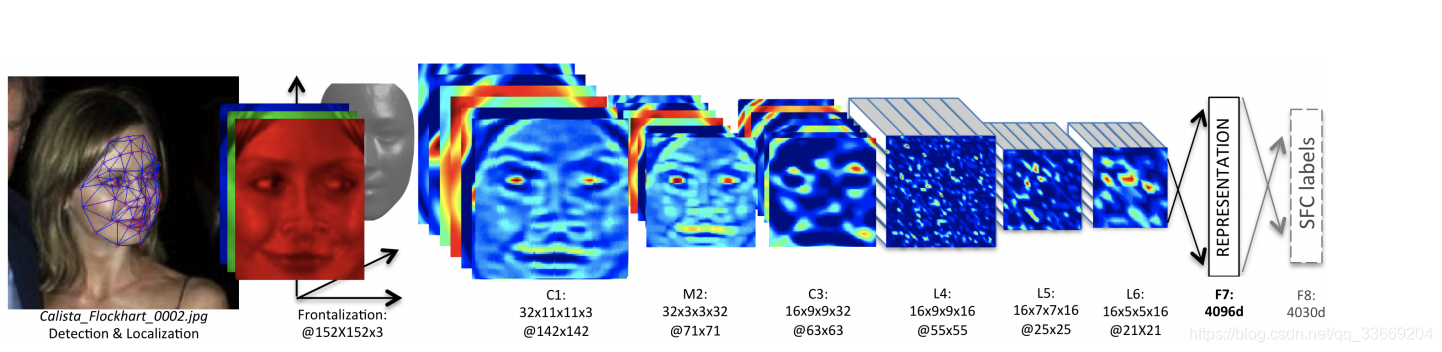該網路是將輸入影象分析為一個向量，通過比較兩個向量的相似度來分析是否是同一個人。 也就是說 $d(x^{(1)}, x^{(2)}) = || f(x^{(1)}) - f(x^{(2)})||^2_2$ 通過 $d$ 的大小來反映兩張圖片中人臉的相似度。 如果 $x^{(i)}$，$x^{(j)}$來自同一個人，那麼 $||f(x^{(i)}) - f(x^{(j)})||^2$

很小，反之如果 $x^{(i)}$，$x^{(j)}$來自不同人，那麼 $||f(x^{(i)}) - f(x^{(j)})||^2$很大。 論文地址：https://www.cv-foundation.org/openaccess/content_cvpr_2014/papers/Taigman_DeepFace_Closing_the_2014_CVPR_paper.pdf

Triplet loss

這裡提出了一種損失函式的構造方法。 給出三張圖片，一張為樣本圖片（anchor），一張為同一個人的另一張圖片（positive），一張為不同人的圖片（negative），這些圖片在通過sigmese網路之後，我們希望這三張圖片的輸出滿足 $\mathrm{\mid }$

∣f(A)−f(P)∣∣2+α≤∣∣f(A)−f(N)∣∣2 ||f(A) - f(P)||^2 + \alpha \le || f(A) - f(N)||^2 這裡新增 $\alpha$ 的原因是為了拉大 $A\to P$ 與 $A\to N$ 之間的差距（這裡與支援向量機的處理類似，感興趣可以看另一篇部落格 https://blog.csdn.net/qq_33669204/article/details/83239793 ）。 該式也等於 $||f(A) - f(P)||^2 - || f(A) - f(N)||^2 + \alpha \le 0$ 這樣 $\alpha$ 也可以避免所有的編碼的輸出都等於0。 所以loss function可以定義為 $\mathcal{L}(A,P,N) = \max(||f(A) - f(P)||^2 - ||f(A) - f(N) ||^2 + \alpha, 0)$ $\mathcal{J} = \sum_{i=1}^m \mathcal{L}(A^{(i)}, P^{(i)}, N^{(i)})$ 通過 $\mathcal{L}(A,P,N)$ 的定義我們可以知道三張圖片的 $\mathcal{L}$一定是一個大於等於0的值，我們希望來自相同人向量之間的差距小於來自不同人向量之間的差距，但這樣又會使loss function小於0違背了loss function必須大於等於0的原則，因此需要新增一個Max函式。 在構築資料集時也應該注意由於我們需要 A和 P，因此在資料集中應該有來自同一個人的不同圖片，在挑選 A，P，N時也應該注意如果我們隨機選，那麼兩個差距很大的人很容易滿足loss function，因此挑選時儘量使A和P的差距不大即 $d(A, P) \approx d(A, N)$ 訓練時應該使用別人開源的預訓練模型來加快訓練，不要從頭開始。 論文地址：https://www.cv-foundation.org/openaccess/content_cvpr_2015/papers/Schroff_FaceNet_A_Unified_2015_CVPR_paper.pdf

Face verification和二分類

$\hat{y} = \sigma(\sum_{k=1}^n \omega_k|f(x^{(i)})_k - f(x^{(j)})_k| + b)$ 上式表示第 i 張圖片和第 j 張圖片之間的差距，使用sigmoid函式啟用後判斷兩張圖片是否來自一個人。

Neural style transfer

卷積神經網路視覺化

這裡提出了一個很重要的概念：卷積視覺化，通過理解這個原理，我們可以知道卷積神經網路的每一層在幹什麼。 這裡需要提一下，視訊中的一個隱藏單元是指一個卷積核，也就是卷積層中的一個channel。 由視訊中我們可以知道，隨著網路層數的加深，一個隱藏單元啟用的部分對應的特徵越來越大（從邊緣特徵到物體的整個特徵），這一方面打算詳細讀一下論文再討論，現在只理解了大概，總感覺有些問題。 論文地址：https://arxiv.org/pdf/1311.2901.pdf

Content cost function

$J(G) = \alpha J_{context}(C,G) + \beta J_{style}(S,G)$ 基於這個式子，我們可以知道風格轉換需要同時考慮內容與風格上的相似度，假設 $\alpha^{[l](C)}$ 與 $\alpha^{[l](G)}$ 是卷積層的啟用值，如果這兩個值相似，那麼就說明卷積網路的輸出可以保證在內容上與內容圖片相似。

Content

我們可以通過 $J_{context}(C,G) = \frac{1}{2}||\alpha^{[l](C)} - \alpha^{[l](G)}||^2$ 求解。

Style

在求解style的cost function之前需要先定義一些名詞：

1. 風格：不同channel之間的關聯程度
2. 相關係數：同一個地方出現兩種channel表示特徵的可能性

通過這兩個定義我們可以知道風格也就是不同channel之間相關係數的反映。 假設 $a_{i,j,k}^{[l](S)}$ 為第 $l$ 層卷積在 $(i,j,k)$ 處的啟用值， $G^{[l]}$ 為當前層的相關值矩陣（G是指 gran matrix），大小為 $n_c^{[l]} \times n_c^{[l]}$，$G^{[l]}$ 在$(k,k')$處相關值為 $G_{kk'}^{[l](S)} = \sum_{i=1}^{n_H^{[l]}}\sum_{j=1}^{n_w^[[l]}a_{ijk}^{[l](S)}a_{ijk'}^{[l](S)}$ 上式表示輸入風格影象的相關值矩陣 $G_{kk'}^{[l](G)} = \sum_$