May 3, 2017

我們已經瞭解了幾種其他的一些生成模型，並且解釋了GAN與這些模型的工作方式是不同的，那麼GAN是如何工作的？

3.1 GAN 框架

GAN的基本思想是兩個玩家共同參與的二人零和博弈。 其中一個叫生成器。 生成器試圖生成與訓練樣本相同分佈的樣本。 另一個玩家是判別器。 判別器用來判別樣本的真偽。 判別器使用傳統的監督學習的方法，將輸入分類為真和假兩個類。 生成器被優化來試圖欺騙判別器。 舉個例子來說， 生成器類似於假幣制造者，他試圖製作假幣， 判別器類似於警察， 他試圖判別真幣和假幣。 為了在博弈中取得成功， 造假者必須學習製造能夠以假亂真的假幣， 意味著生成器必須學習生成與訓練資料有同樣分佈的樣本。 圖12展示了這個過程。

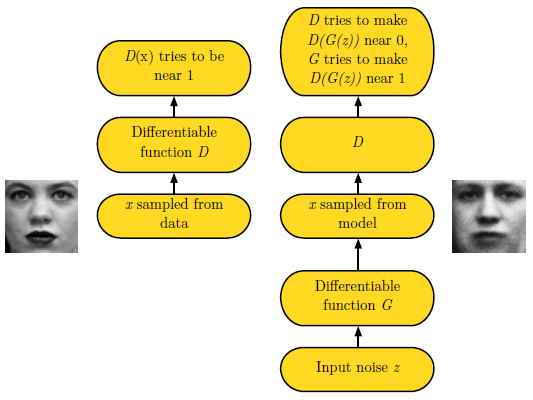
圖12： GAN設計為兩個對抗的玩家在同一個博弈遊戲中互相對抗。 玩家被描述為由一組引數組成的可微函式。 通常情況下，這些函式都使用深度神經網路。 這個博弈可以被展開為兩個場景。 第一個場景， 隨機的從訓練資料集中取樣xx, 取樣的資料作為判別器DD的輸入。 判別器的目的是預測樣本是真實樣本的概率， 此判決假設輸入的樣本一半是真樣本，另一半是偽樣本。 在此場景中， 判別器的目標是讓D(x)D(x)趨近於1。 第二個場景， 生成器的輸入是隱變數zz， 此隱變數根據模型的一個先驗分佈進行隨機取樣。 然後， 生成器生成的偽樣本G(z)G(z)被輸入到判別器中。 在這個場景中， 兩個玩家都在參與。 判別器試圖讓D(G(z))D(G(z))趨近於0， 生成器試圖讓其趨近於1。 如果兩個模型具備足夠的能力，那麼最終博弈將達到納什均衡， 也就是G(z)G(z)的生成樣本將符合訓練資料的分佈， 並且對所有的xx, D(x)=1/2D(x)=1/2。

形式上， GAN是包含隱變數zz以及觀測變數xx的結構化概率模型。 （參考Goodfellow et al, (2016) 第16章關於結構化概率模型的介紹） 圖13給出了此圖形結構。

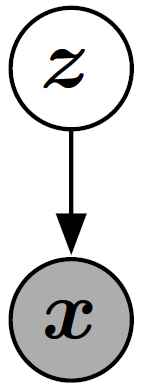
圖13： GAN的圖形化模型結構， 類似於VAEs， sparse coding, 等等。 它是一種直接的影象化模型也就是每一個隱變數影響每一個觀測變數。 有些GAN變種去除了一些此種連結。

兩個玩家被描述為兩個函式， 每一個函式對輸入和引數都是可微的。 判別器是函式DD， 輸入是xx, 引數是θ(D)θ(D)。 生成器被定義為函式GG, 輸入是zz, 引數是θ(G)θ(G)。

兩個玩家的損失函式都對應著各自的引數。 判別器希望最小化J(D)(θ(D),θ(G))J(D)(θ(D),θ(G))但是隻能通過對θ(D)θ(D)的控制完成。 同樣的生成器希望最小化J(G)(θ(D),θ(G))J(G)(θ(D),θ(G))但是隻能通過對θ(G)θ(G)的控制完成。 兩個玩家的損失函式都受另一個玩家的引數影響， 但是卻不能控制對方的引數， 這個場景更像是一個博弈遊戲而不是一個優化問題。 優化問題的解是一個（區域性）最小化問題， 也就是指一個引數空間的點，其鄰近的點的損失都大於或者等於此點。 此問題在博弈中是一個納什均衡問題。 這裡我們使用的方法被稱為區域性微分納什均衡(Ratliff et al., 2013)。 在本文中， 我們使用一個數組(θ(D),θ(G))(θ(D),θ(G))來表述納什均衡， 其中對引數θ(D)θ(D)區域性最小化J(D)J(D)， 對引數θ(G)θ(G)區域性最小化J(G)J(G)。

生成器 生成器是一個簡單的可微函式GG。 zz根據一個簡單的先驗分佈來取樣， G(z)G(z)根據pmodelpmodel生成樣本xx。 通常， GG使用深度神經網路模型。 GG的輸入不一定對應著第一層， 輸入可能在任何的網路層中。 比如說， 我們可以將zz分為兩個向量， z(1)z(1), z(2)z(2), 然後z(1)z(1)可以作為第一層的輸入， z(2)z(2)作為最後一層的輸入。 如果z(2)z(2)是高斯分佈的，那麼xx就是一個給定z(1)z(1)的條件高斯分佈。 另一個流行的策略是將額外的或者相乘噪音加入到隱含層中，或將噪音與網路的隱含層進行連線使用。 總之，我們可以看到生成器網路的設計有很少的限制。 如果我們希望pmodelpmodel完全的支援xx空間，那麼我們需要zz的維數至少要和xx一樣大, 並且GG是可微的， 以上為設計所需要的所有的條件。 特別是， 任何的非線性ICA方法可以使用的模型都可以作為GAN的生成器網路。 GAN與微分autoencoder的關係相對比較複雜； 有些GAN可以訓練的一些模型，VAE不能訓練， 反之也一樣。 但是這兩個架構也有很多的交叉。 最大的不同是，當使用標準的反向傳遞優化時， VAE不能使用離散變數作為輸入， 但是GAN不能有離散變數的輸出。

訓練過程 訓練過程包含同步SGD。 每一步訓練有兩個minibatch被取樣： 一個是xx取樣自訓練資料，另一個是zz取樣自模型的隱變數先驗。 然後兩個求導過程被同時執行： 一個是更新θ(D)θ(D)來最小化J(D)J(D), 另一個是更新θ(G)θ(G)來最小化J(G)J(G)。 在這兩個情況下， 你可以使用基於求導的優化演算法。 Adam是一個好的選擇。 很多作者推薦對其中一個玩家進行更多步的優化。 但是直到2016年底， 作者的意見（經驗）是，實際應用中執行的比較好的方案是： 使用同步梯度下降，並對每一個玩家分別進行單步優化。

3.2 損失函式

有很多不同的損失函式可以被用於GAN的架構中。

3.2.1 判別器的損失函式 J(D)J(D)

很多GAN相關的工作，都使用了相同的判別器損失函式， 也就是J(D)J(D)。 區別之處是使用了不同的生成器的損失函式，也就是J(G)J(G)。 判別器的損失函式被定義為：

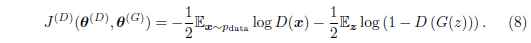
這是一個標準的交叉熵損失函式， 此函式使用sigmoid的輸出。 通過訓練一個標準的兩類分類問題來最小化損失函式。 不同之處是此分類器使用兩個minibatch的資料來訓練； 一個來自訓練資料， 對應標籤1， 另一個來自生成器，對應標籤0。

所有GAN的版本都鼓勵判別器來最小化方程式8。 在所有的版本中， 判別器都使用了相同的優化策略。 讀者可以去完成7.1章的練習，答案在8.1章。 這個練習讓我們瞭解如何得到最優的判別器優化策略， 並且討論了此策略構成的重要性。

通過訓練判別器， 我們可以得到對每一個xx的比值的估計， 也就是方程式9：

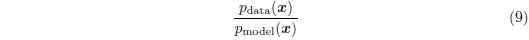
通過估計這個比值可以讓我們計算多樣的方差和其梯度。 此種優化是GAN區別於變分autoencoder和玻爾茲曼機的主要近似技術。 其他的深度生成模型基於下邊界或者馬爾可夫鏈來優化來近似； GAN使用監督學習優化來估計兩個密度的比值來近似。 GAN優化受到監督學習過擬合和訓練不足問題的影響。 理論上， 通過完美的優化和使用足夠多的資料可以克服此問題。 使用其他優化方法的其他的生成式模型也有他們各自的一些問題。

使用博弈理論工具對GAN進行分析顯得更加的自然， 我們稱GAN為“對抗的”。 但是我們也可以認為他們是合作的， 在這種情況下，判別器估計密度的比例， 然後可以自由的與生成器分析這些資訊。 從這一點上看， 判別器更像一個老師指導生成器如何提高自己並且超過對手。 當然，合作的觀點沒有在數學表達上有任何改變。

3.2.2 Minimax（極小極大， 極大中的極小）

到此為止，我們詳述了判別器的損失函式。 完整的描述此博弈遊戲也需要我們詳述生成器的損失函式。

此博弈的最簡單的版本是零和博弈， 也就是所有玩家的損失之和永遠是零， 此博弈可以描述為：

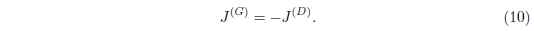
因為J(G)J(G)是被直接繫結到J(D)J(D)上的， 所以我們可以通過一個描述判別器報酬的價值函式來歸納這個完整的博弈遊戲：

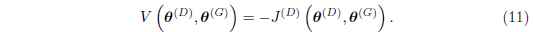
零和博弈經常被稱為極小極大博弈，因為這個方案包含一個外迴圈的最小化，和一個內迴圈的最大化：

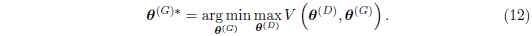
極小極大博弈最受關注是因為他在理論上容易控制。 Goodfellow et al. (2014b) 使用了GAN的一個變形來展示了這個博弈的學習類似於最小化資料和模型的分佈的Jensen-Shannon散度， 以及只要兩個玩家的策略可以在函式空間被直接更新， 那麼博弈就可以收斂到均衡狀態。 在實際應用中， 玩家被表達為深度神經網路，並且在引數空間被更新， 所以，一些凸問題，不在此列。

3.2.3 啟發式（Heuristic）， 非飽和博弈（non-saturating game）

極小極大博弈中生成器使用的損失函式（方程式10）在理論上分析很有效，但是在實際應用中表現並不好。

最小化目標類和分類器預測分佈的交叉熵是很有效的， 因為只要分類器還有錯誤的輸出，損失函式就不會達到飽和。 當然，損失最終將飽和， 也就是趨近於零， 但是這種情況只會發生在分類器能夠進行正確分類的情況下。

在極小極大博弈中， 判別器最小化交叉熵， 但是生成器最大化同一個交叉熵。 這對生成器來說很不幸， 因為當判別器能夠以很好的置信值成功拒絕生成樣本時， 生成器的梯度將會消失。

為了解決此問題， 一個方式是繼續對生成器使用交叉熵最小化。 我們直接使用目標來構建交叉熵損失函式， 而不是使用判別器的損失來獲取生成器的損失。 所以生成器的損失函式變為：

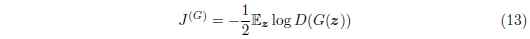
在極小極大博弈中， 生成器最小化判別器的對數概率為真。 在此博弈中， 生成器最大化判別器的對數概率為錯誤。

這個版本的博弈是受到啟發式方法的啟發， 而不是基於理論的分析。 此博弈版本的唯一動機是保證當一個玩家面臨失敗時，也可以有一個穩定的梯度。

此博弈版本， 博弈不再是零和， 並且不能使用一個單一的值函式來描述。

3.2.4 最大似然博弈（Maximum likelihood game）

我們可能喜歡使用最大似然方法來優化GAN， 這樣意味著最小化資料和模型分佈的KL散度， 如方程式4. 另外，在第二章中，我們討論過為了簡化與其他方法的比較，GAN可以選擇使用最大似然來優化。

在GAN的框架中， 有很多的方法可以優化方程式4。 Goodfellow （2014） 展示了使用：

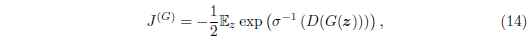
σσ是logistic sigmoid函式， 當基於判別器最優假設時， 等價於最小化方程式4。 此等價保證了預期的優化： 在實際應用中， 因為我們使用取樣資料（也就是說取樣xx為了最大似然優化， 取樣zz為了GAN優化）來對梯度進行估計， 所以會導致KL散度的隨機梯度下降以及GAN訓練過程的梯度與真實的期望梯度有一些擾動。 關於此等價的練習題，請參考7.3章， 答案在8.3章。

在GAN框架中，使用其他的近似最大似然的方法也是可能的， 比如說Nowozin et al. (2016).

3.2.5 散度的選擇是否是GAN的可區分特徵

作為我們調查GAN是如何工作的一部分， 我們可能好奇是什麼讓GAN在生成圖片任務中表現的如此好。

以前， 很多人（包括作者本人）相信GAN能夠提供銳化，很真實的樣本，是因為他最小化Jensen-Shannon散度， 而VAE產生模糊的樣本因為他們最小化資料和模型的KL散度。

KL散度不是對稱的； 最小化DKL(pmodel||pdata)DKL(pmodel||pdata)與最小化DKL(pdata||pmodel)DKL(pdata||pmodel)是不同的。 最大似然估計執行的是前者， 最小化Jensen-Shannon散度更像是優化後者。 如圖14所示， 後者可能會生成更好的樣本， 因為使用此方差訓練的模型更傾向於生成符合訓練資料分佈的樣本， 即便是那意味著忽略了一些mode（眾數）， 而不是包括所有的mode，使生成的樣本不符合任何訓練集的mode。

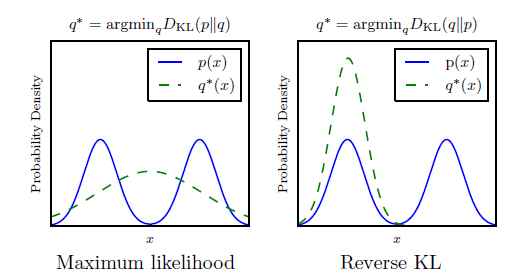
圖14： KL散度的兩個表達不是等價的。 最明顯的不同是當模型擬合數據分佈的能力很差時。 這裡展示了一個一維資料xx分佈的例子。 在這個例子中， 資料分佈是兩個混合的高斯分佈的組合， 模型使用一個單一的高斯模型。 因為一個單一的高斯分佈不能準確的表達真實的資料分佈， 散度的選擇將決定模型的選擇。 左邊的圖使用了最大似然測度。 此模型選擇對這兩個mode進行平均處理， 因此它側重於對兩者整體的概率最大化。 右邊的圖， 使用相反順序引數的KL散度。 我們可以認為DKL(pdata||pmodel)DKL(pdata||pmodel)傾向於對所有資料分佈的整體都提高概率， 而DKL(pmodel||pdata)DKL(pmodel||pdata)側重於降低資料不存在區域的概率。 通過這種觀察， 使我們期待DKL(pmodel||pdata)DKL(pmodel||pdata)能夠產生更好看的樣本，因為模型將不會選擇產生分佈在資料的兩種mode之間的非正常樣本。

一些新的證據表明使用Jensen-Shannon散度不能解釋為什麼GAN會產生銳化的樣本：

• 現在使用最大似然也能來訓練GAN， 如3.2.4章描述的。 這些模型仍然可以生成銳化樣本， 並且選擇比較少的mode。 如圖15。

  

  圖15： f-GAN模型能夠最小化很多不同的散度。 因為模型被訓練最小化DKL(pdata||pmodel)DKL(pdata||pmodel)並且仍然可以產生銳化的樣本， 並且傾向於選擇少量的mode， 我們可以總結為使用Jensen-Shannon散度不是GAN的特別重要的一個特徵， 並且它也不能解釋為什麼GAN的樣本會傾向於銳化。

• GAN經常可以通過使用很少的mode就可以生成資料； 少於由於模型能力而限制的數量。 反向KL傾向於使用模型可以做到的儘可能多的mode來生成資料。 這說明mode collapse是由於一個其它的因素而不是由於散度選擇造成的。

總之， GAN之所以選擇少量的mode來生成資料， 是因為訓練過程的一些缺點， 而不是因為要最小化的散度引起的。 我們將在第5.1.1章中進一步介紹。 GAN產生銳化影象的原因還沒有完全的明確。 可能是因為使用GAN訓練的這類模型與使用VAE訓練的模型不同 （比如， 當xx有一個更加複雜的分佈，而不是一個簡單的高斯分佈時， 使用GAN更容易構建模型）。 也可能是因為GAN的近似處理與其他方法的近似有不同的影響。

3.2.6 損失函式比較

我們可以認為生成器網路是通過一些特殊的增強學習來訓練的。 與其說它是在讓一個特定的輸出xx與一個zz相關聯， 還不如說是生成器採取一些行動，並且接收這些行動來帶來的反饋（獎勵）。 特別是， J(G)J(G)根本不直接參考訓練資料； 所有的關於訓練資料的的資訊都是僅僅通過判別器反饋的資訊來進行學習的 （附帶著， 這將使得GAN更不容易過擬合， 因為生成器不會直接的複製訓練資料）。 其學習過程與傳統的增強學習不一樣， 這是因為：

• 生成器不僅可以觀察回報函式的輸出，並且可以獲得它的梯度。
• 回報函式是非穩定的； 回報是通過判別器對生成器策略改變的反應來獲取的。

在所有情況下， 我們可以認為取樣過程開始於選擇一個特定的zz, 然後進行獨立的處理並接受對應的的回報， 也就是說與其他的zz的相關行為無關。 生成器得到的反饋是一個標量函式，D(G(z))D(G(z))。 我們通常認為這與損失有關（負的回報）。 生成器的損失（D(G(z))D(G(z))）總是單調下降的， 但是不同的博弈被設計為使損失沿著不同的曲線快速下降。

圖16展示了三個不同變種的GAN的損失曲線，也就是D(G(z))D(G(z))的曲線。 我們可以看到， 最大似然方法的損失函式有很高的方差， 因為大多數的損失的梯度來自很少樣本(這些zz對應著的樣本更像是真而不像偽樣本)。 啟發式非飽和的損失函式有很低的樣本方差， 這可以解釋為什麼在實際應用中很成功。 這告訴我們減少方差的技術是提高GAN表現的很重要的研究領域， 特別是基於最大似然的GAN。

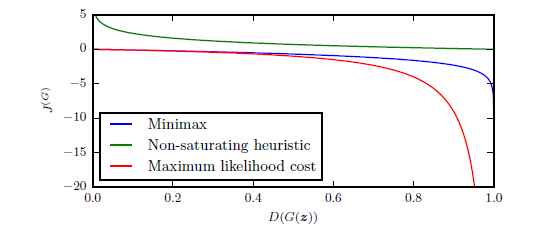
圖16： 生成器接受的關於樣本G(z)G(z)的損失只取決於判別器對此樣本的反饋。 判別器將其識別為真樣本的概率越高，那麼生成器接受到的損失就越小。 我們可以看到當樣本更像假樣本時， minimax和最大似然都會有一個很小的梯度， 我們可以看到左邊是很平坦的曲線。 啟發式非飽和方法避免了此問題。 最大似然還受到絕大多數梯度值只是來自於很少的樣本，如右邊的曲線， 這意味著很少的樣本影響了minibatch的梯度計算。 這告訴我們減少方差的技術是提高GAN表現的很重的研究領域， 特別是使用最大似然的GAN。

3.3 DCGAN結構

當前多數的GAN都基於DCGAN的結構 （Radford et al., 2015）。 DCGAN是“深度，卷積GAN”， 儘管在DCGAN以前，GAN也是使用深度和卷積網路的， DCGAN被用來指這個特定的結構。 DCGAN結構的一些主要的觀點有：

• 在判別器和生成器的多數層中都使用Batch normalization(Ioffe and Szegedy, 2015)， 判別器的兩個minibatch被分別的標準化。 生成器的最後層和第一層沒有使用batch normalization， 因此此模型可以學習到正確的資料分佈的平均，縮放。 看圖17.
• 整體網路結構借鑑了全卷積網路（Springenberg et al., 2015）。 這個結構即包含pooling 也包含unpooling層。 當生成器需要提高表達的空間維度時， 它使用stride大於1的轉置卷積網路.
• 使用Ada優化器，而不是SGD加衝量。

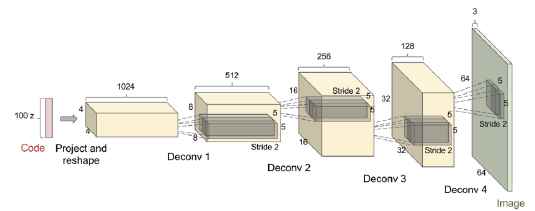
圖17： DCGAN使用的生成器網路。 圖來自Radford et al. (2015).

在DCGAN以前， LAPGAN（Denton et al., 2015）是唯一的可以處理（縮放）高解析度影象的GAN版本。 LAPGAN需要一個多階段的生成過程， 多個GAN生成多個不同層次的Laplacian金字塔來表達影象的細節。 DCGAN是第一個使用a single shot的方式來生成高解析度影象的GAN模型。 如圖18所示， 當限制影象的類別時DCGAN可以生成很高質量的影象， 比如說臥室影象。 DCGAN也清晰的展示了， GAN可以學習以有意義的方式來使用隱程式碼， 如圖19所示， 對幾個潛在空間的簡單的算術操作（加，減等）可以有很明確的對應著其輸入的語義上的解釋。

圖18： DCGAN生成的一些臥室影象， 使用LSUN資料集訓練。

圖19： DCGAN展示了GAN可以學習分散式表徵，也就是可以區別性別資訊和戴眼鏡的資訊。 假設有一個戴眼鏡的男人的向量， 減去用來表達不帶眼鏡男人的向量， 最後加上表達不戴眼鏡女人的向量， 就可以得到一個戴眼鏡女人的向量。 生成模型正確的解碼了所有的這些表達的向量， 並且這些被解碼的向量可以被認為屬於正確的類。 此圖片來自Radford et al. (2015).

3.4 GAN與NCE和最大似然的關係

當我們試圖去理解GAN是如何工作時， 我們可能想知道他與noise-contrastive estimation（NCE）的聯絡 （Gutmann and Hyvarinen, 2010）。 Minimax GAN使用來自NCE的損失函式作為他們的價值函式， 因此這兩個方法好像很相近。 但實際上，他們學習非常不同的事情， 因為這兩個方法針對的是博弈中不同的玩家。 簡單的說， NCE的目標是學習判別器的密度模型， 但是GAN的目標是學習取樣器來定義生成器。 這兩個任務在定性分析來看是很相近的， 其實，兩個任務的梯度實際上很不相同。 驚奇的是，最大似然估計（MLE）與NCE很相似， 並且在minimax博弈中有著一樣的價值函式， 但是對其中的一個玩家使用了一系列啟發式的更新策略而不是梯度下降。 圖20總結了他們的關係。

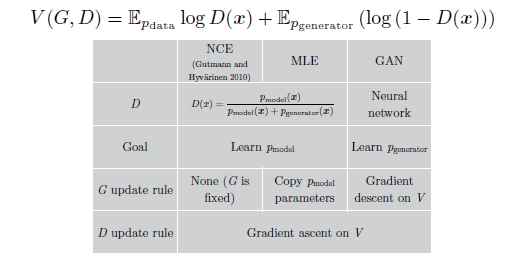
圖20： Goodfellow（2014）展示了NCE,MLE,GAN的關係： 所有三種方法可以被解釋為使用一樣的價值函式來訓練minimax博弈。 最大的不同是pmodelpmodel的分佈。 對GAN來說， 生成器是pmodelpmodel, 但是NCE, MLE是指判別器。 除了這些， 還有更新策略的不同。 GAN學習兩個玩家通過梯度下降。 MLE學習判別器也是使用梯度下降， 但是它為生成器使用了一個啟發式的更新規則。 特別是， 在每一次判別器更新步驟以後， MLE將學習到的判別器的密度模型複製並將其轉換為一個取樣器，從而作為生成器來使用。 NCE從來不更新生成器， 他的生成器直接使用一個固定的噪音。

[最終修改於： 2017年6月9日]