利用mlxtend進行資料關聯分析
今天本該是個剁手的日子,只可惜餘額不足高攀不起那臺i7-8565,只有再寫一篇文章聊以慰籍~~
前言:之前很少做關於資料關聯分析的題,而當初學關聯分析時也是自己寫程式碼來實現底層轉換與運算,粗略一點的整體程式碼量也達到150行左右,所以沒有高階的開源工具使用是很費時間的,由此阻礙了一顆想學習的心。後來遇到相關問題便Google了一些解決辦法,其中有一個整合很優秀,使用也很方便的GitHub開源專案,也是本篇文章的重點——
首先簡單介紹一下關聯分析的三個相關知識點:

頻繁項集:
頻繁項集是指那些經常出現在一起的物品,例如上圖的{葡萄酒、尿布、豆奶},從上面的資料集中也可以找到尿布->葡萄酒的關聯規則,這意味著有人買了尿布,那很有可能他也會購買葡萄酒。那如何定義和表示頻繁項集和關聯規則呢?這裡引入支援度和可信度(置信度)。
支援度:
支援度:一個項集的支援度被定義為資料集中包含該項集的記錄所佔的比例,上圖中,豆奶的支援度為4/5,(豆奶、尿布)為3/5。支援度是針對項集來說的,因此可以定義一個最小支援度,只保留最小支援度的項集。
置信度:
可信度(置信度):針對如{尿布}->{葡萄酒}這樣的關聯規則來定義的。計算為 支援度{尿布,葡萄酒}/支援度{尿布},尿布,{葡萄酒}的支援度為3/5,{尿布}的支援度為4/5,所以“尿布->葡萄酒”的可行度為3/4=0.75,這意味著尿布的記錄中,我們的規則有75%都適用(買了尿布的顧客有75%還會買葡萄酒)。
上面簡單介紹三個基本概念,下面我們就來利用 mlxtend 完整簡單的實現上面購物表單的關聯分析問題。
關聯分析示例:
首先建立資料:
轉換為DataFrame格式,然後再教一個後續轉換回來的方法。
import pandas as pd
shopping_list = [['豆奶','萵苣'],
['萵苣','尿布','葡萄酒','甜菜'],
['豆奶','尿布','葡萄酒','橙汁'],
['萵苣','豆奶','尿布','葡萄酒'],
['萵苣','豆奶','尿布','橙汁']]
shopping_df = pd.DataFrame(shopping_list)轉換資料列表:
接著轉換DataFrame資料為包含資料的列表。(由於我們接觸到的可能是DataFrame資料所以這裡介紹了兩個轉換為上面列表的方法)
# df_arr = shopping_df.stack().groupby(level=0).apply(list).tolist() # 方法一
def deal(data):
return data.dropna().tolist()
df_arr = shopping_df.apply(deal,axis=1).tolist() # 方法二轉換為模型可接受資料:
由於mlxtend的模型只接受特定的資料格式。(TransactionEncoder類似於獨熱編碼,每個值轉換為一個唯一的bool值)
from mlxtend.preprocessing import TransactionEncoder # 傳入模型的資料需要滿足特定的格式,可以用這種方法來轉換為bool值,也可以用函式轉換為0、1
te = TransactionEncoder() # 定義模型
df_tf = te.fit_transform(df_arr)
# df_01 = df_tf.astype('int') # 將 True、False 轉換為 0、1 # 官方給的其它方法
# df_name = te.inverse_transform(df_tf) # 將編碼值再次轉化為原來的商品名
df = pd.DataFrame(df_tf,columns=te.columns_)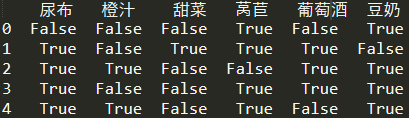
求頻繁項集:
匯入apriori方法設定最小支援度min_support=0.05求頻繁項集,還能選擇出長度大於x的頻繁項集。
from mlxtend.frequent_patterns import apriori
frequent_itemsets = apriori(df,min_support=0.05,use_colnames=True) # use_colnames=True表示使用元素名字,預設的False使用列名代表元素
# frequent_itemsets = apriori(df,min_support=0.05)
frequent_itemsets.sort_values(by='support',ascending=False,inplace=True) # 頻繁項集可以按支援度排序
# print(frequent_itemsets[frequent_itemsets.itemsets.apply(lambda x: len(x)) >= 2]) # 選擇長度 >=2 的頻繁項集求關聯規則:
匯入association_rules方法判斷'confidence'大於0.9,求關聯規則。
from mlxtend.frequent_patterns import association_rules
association_rule = association_rules(frequent_itemsets,metric='confidence',min_threshold=0.9) # metric可以有很多的度量選項,返回的表列名都可以作為引數
association_rule.sort_values(by='leverage',ascending=False,inplace=True) #關聯規則可以按leverage排序
# print(association_rule)下面便得到了上表中滿足設定條件的關聯規則
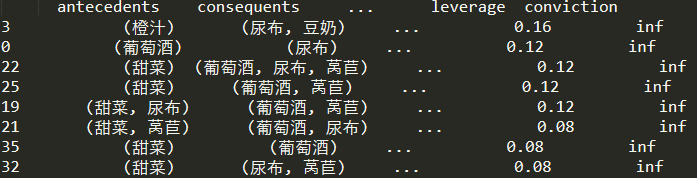

mlxtend使用了 DataFrame 方式來描述關聯規則,而不是 —> 符號,其中:
-
antecedents:規則先導項 -
consequents:規則後繼項 -
antecedent support:規則先導項支援度 -
consequent support:規則後繼項支援度 -
support:規則支援度 (前項後項並集的支援度) -
confidence:規則置信度 (規則置信度:規則支援度support / 規則先導項) -
lift:規則提升度,表示含有先導項條件下同時含有後繼項的概率,與後繼項總體發生的概率之比。 -
leverage:規則槓桿率,表示當先導項與後繼項獨立分佈時,先導項與後繼項一起出現的次數比預期多多少。 -
conviction:規則確信度,與提升度類似,但用差值表示。
提升度計算公式:
其中,當先導項與後繼項獨立分佈時,值為 1,提升度越大,表示先導項與後繼項的關聯性越強。
槓桿率計算公式:
確信度計算公式:
確信度值越大,則先導項與後繼項的關聯性越強。 以上三個值都是越大關聯強度也就越大。
