陣列、佇列、堆、棧、連結串列、樹、圖
他們都是一種儲存資料的方式而已，打個比方，你坐地鐵1號線上班和2號線上班，都能上班只是路線不一樣，他們都是儲存資料的格式，每種資料結構有自己的特點，使用哪種資料格式需要根據具體的需求來選，比如你現在需要有序的儲存一組資料而且還要經常的查詢資料，那麼陣列就是最合適的，他有角標可以很容易進行排序和查詢！如果有序但是經常增刪資料，那麼連結串列就是最合適的，他的增刪很快，但是查詢差。每種資料結構有各自的適用條件，根據需求來選擇具體的資料結構
程式 = 演算法 + 資料結構 資料結構是計算機儲存、組織資料的方式。 資料結構是指相互之間存在一種或多種特定關係的資料元素的集合。 通常情況下，精心選擇的資料結構可以帶來更高的執行或者儲存效率。 資料結構往往同高效的檢索演算法和索引技術有關。
- 佇列
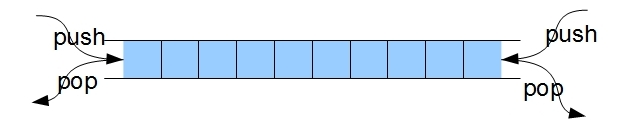
佇列實現了先入先出的語義 (FIFO) 。佇列也可以使用陣列和連結串列來實現：
佇列只允許在隊尾新增資料，在隊頭刪除資料。但是可以檢視隊頭和隊尾的資料。還有一種是雙端佇列，在兩端都可以插入和刪除：
- 陣列
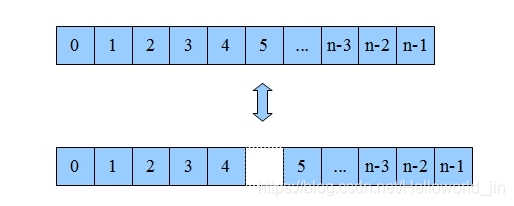
陣列是最最基本的資料結構，很多語言都內建支援陣列。陣列是使用一塊連續的記憶體空間儲存資料，儲存的資料的個數在分配記憶體的時候就是確定的：
訪問陣列中第 n 個數據的時間花費是 O(1) 但是要在陣列中查詢一個指定的資料則是 O(N)。當向陣列中插入或者刪除資料的時候，最好的情況是在陣列的末尾進行操作，時間複雜度是O(1) ，但是最壞情況是插入或者刪除第一個資料，時間複雜度是 O(N) 。在陣列的任意位置插入或者刪除資料的時候，後面的資料全部需要移動，移動的資料還是和資料個數有關所以總體的時間複雜度仍然是 O(N) 。
- 堆(heap) 堆可以看成一棵按順序排列的完全二叉樹，根節點可以為大於等於任何子節點（也可以小於等於任意子節點，看具體的排序方法），在存取時沒有任何限制，可以隨意的訪問某一個子節點。 最大堆:每個節點的值都大於等於它的孩子節點。 最小堆:每個節點的值都小於等於它的孩子節點。
堆的儲存： 可以理解為二叉樹的一種，是節點間有序關係的完全二叉樹，所以可以用陣列來表示。 對於下標為i的節點，它的子樹的左節點的下標為2i,右節點為2i+1，父親的節點下標為i/2（向下取整）。 在程式設計中，使用位運算來代替直接*2可以提高執行速度。- 某些編譯器中會把一些特定的乘法運算改寫為位運算。
-
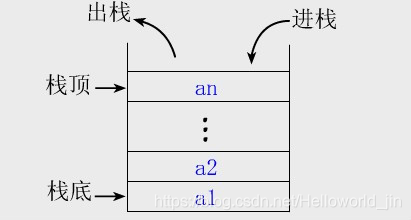
棧(stack) 棧或者稱為堆疊（stack），可以看成是一些堆起來的盤子，桶狀線性資料結構。但是棧是受限制的線性資料結構，只允許先進後出，並且只能在棧頂進行插入刪除操作。 先進後出(FILO)
-
連結串列 連結串列是在非連續的記憶體單元中儲存資料，並且通過指標將各個記憶體單元連結在一起，最有一個節點的指標指向 NULL 。連結串列不需要提前分配固定大小儲存空間，當需要儲存資料的時候分配一塊記憶體並將這塊記憶體插入連結串列中。
在連結串列中查詢第 n 個數據以及查詢指定的資料的時間複雜度是 O(N) ，但是插入和刪除資料的時間複雜度是 O(1) ，因為只需要調整指標就可以：
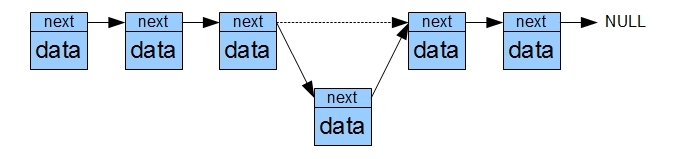向上面這樣的連結串列結構在插入和刪除的時候程式設計會比較困難，因為需要記住當前節點的前一個節點，這樣才能完成插入和刪除。為了簡便通常使用帶有頭節點的連結串列：
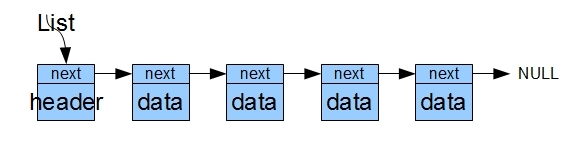上面的連結串列是單鏈表，此外還有雙鏈表，就是節點中包含指向下一個節點的指標和指向上一個節點的指標：
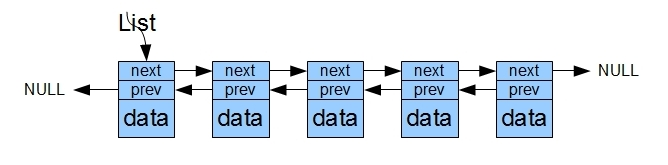不帶有頭節點的雙向連結串列在插入和刪除資料的時候也不會出現單鏈表那樣的問題。此外還有一種連結串列是迴圈連結串列，它是將雙向連結串列的頭尾相接：
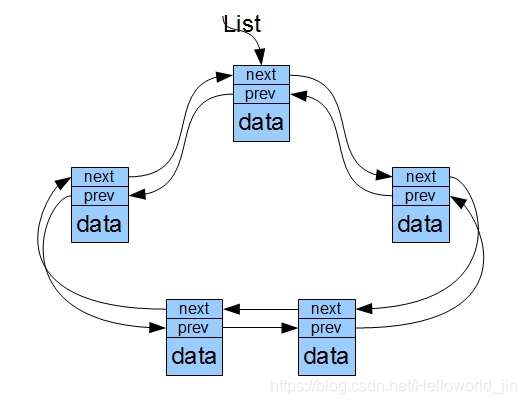向迴圈雙向連結串列和迴圈連結串列中插入或者從中刪除資料只是多移動幾個指標。 -
樹 它是由n（n>=1）個有限結點組成一個具有層次關係的集合。把它叫做“樹”是因為它看起來像一棵倒掛的樹，也就是說它是根朝上，而葉朝下的。它具有以下的特點： 每個結點有零個或多個子結點；沒有父結點的結點稱為根結點；每一個非根結點有且只有一個父結點；除了根結點外，每個子結點可以分為多個不相交的子樹； 樹也可以這樣定義：樹是由根結點和若干顆子樹構成的。樹是由一個集合以及在該集合上定義的一種關係構成的。集合中的元素稱為樹的結點，所定義的關係稱為父子關係。父子關係在樹的結點之間建立了一個層次結構。在這種層次結構中有一個結點具有特殊的地位，這個結點稱為該樹的根結點，或稱為樹根。
樹的種類： 無序樹：樹中任意節點的子結點之間沒有順序關係，這種樹稱為無序樹,也稱為自由樹; 有序樹：樹中任意節點的子結點之間有順序關係，這種樹稱為有序樹； 二叉樹：每個節點最多含有兩個子樹的樹稱為二叉樹； 完全二叉樹 滿二叉樹 霍夫曼樹：帶權路徑最短的二叉樹稱為哈夫曼樹或最優二叉樹；
最典型的是二叉樹
、
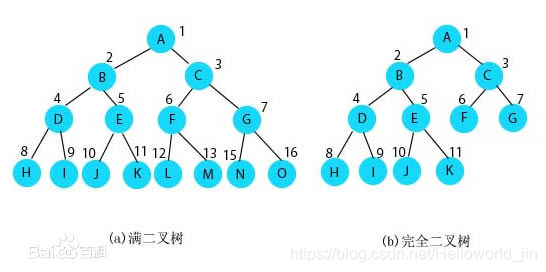7. 圖
圖（Graph）是由頂點的有窮非空集合和頂點之間邊的集合組成，通常表示為：G（V，E），其中，G表示一個圖，V是圖G中頂點的集合，E是圖G中邊的集合。在圖中的資料元素，我們稱之為頂點（Vertex），頂點集合有窮非空。在圖中，任意兩個頂點之間都可能有關係，頂點之間的邏輯關係用邊來表示，邊集可以是空的。
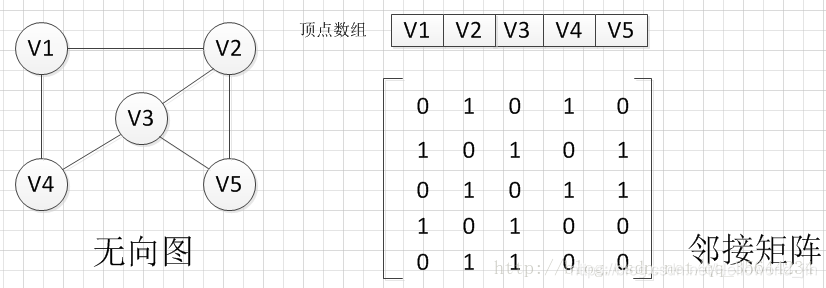
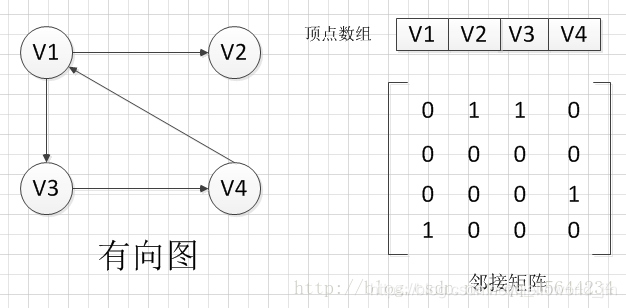
圖按照邊的有無方向分為無向圖和有向圖。無向圖由頂點和邊組成，有向圖由頂點和弧構成。弧有弧尾和弧頭之分，帶箭頭一端為弧頭。
圖按照邊或弧的多少分稀疏圖和稠密圖。如果圖中的任意兩個頂點之間都存在邊叫做完全圖，有向的叫有向完全圖。若無重複的邊或頂點到自身的邊則叫簡單圖。
圖中頂點之間有鄰接點、依附的概念。無向圖頂點的邊數叫做度。有向圖頂點分為入度和出度。
圖上的邊或弧帶有權則稱為網。
圖中頂點間存在路徑，兩頂點存在路徑則說明是連通的，如果路徑最終回到起始點則稱為環，當中不重複的叫簡單路徑。若任意兩頂點都是連通的，則圖就是連通圖，有向則稱為強連通圖。圖中有子圖，若子圖極大連通則就是連通分量，有向的則稱為強連通分量。
無向圖中連通且n個頂點n-1條邊稱為生成樹。有向圖中一頂點入度為0其餘頂點入度為1的叫有向樹。一個有向圖由若干棵有向樹構成生成森林。
圖的儲存結構—-鄰接矩陣
圖由頂點的集合V和頂點之間的關係集合R構成。
例如G1=(V,E)
V={V1,V2,V3,V4,V5}
E={（v1,v2）,(v1,v3)}
表示無向圖中，結點v1和v2相連，v1和v3相連。其中與某結點相連的線段的數目稱為該節點的度。
例如G2=(V,A)
V={V1,V2,V3,V4,V5}
A={<v1,v2>,<v1,v3>}