【說明】本文來自由周世平老師主編的《C語言程式設計》教材。我作為參編人員執筆了第7、8章。“第8章 問題求解與演算法”中“8.6.1 回溯法”以8皇后問題的求解為例，介紹了回溯法的解題過程。這個解決方案中用到了“棧”，引用至此，作為棧應用的例子。需要說明的是，教材面向程式設計初學者，並全文中並未提出過任何關於“棧”的描述。這樣做，隱藏了術語，減少初學者的認知難度。對於資料結構的學習者而言，由於知識面的擴大，卻用不著迴避這樣的術語了。於是，在閱讀本文時，作為體會棧的應用，需要自行從中提取出應用棧式儲存及處理的部分來。

【全文】 　　回溯法是一種通用的搜尋演算法，幾乎可以用於求解任何可計算的問題。演算法的執行過程就像是在迷宮中搜索一條通往出口的路線，總是沿著某一方向向前試探，若能走通，則繼續向前進；如果走不通，則要做上標記，換一個方向再繼續試探，直到得出問題的解，或者所有的可能都試探過為止。 　　下面，用經典的8皇后問題為例來講解如何使用回溯的思想解決問題。

 

　　8皇后問題是：在8×8的棋盤上擺放8個皇后，使其不能互相攻擊，即任意的兩個皇后不能處在同一行，同一列，或同一斜線上。可以把八皇后問題拓展為n皇后問題，即在n×n的棋盤上擺放n個皇后，使其任意兩個皇后都不能處於同一行、同一列或同一斜線上。

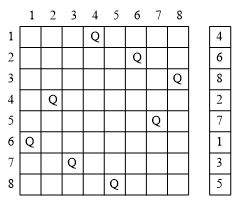
　　首先需要對棋盤進行描述。直觀地，棋盤可以用二維陣列表示，有皇后的棋格對應陣列元素值為1，無皇后的棋格對應陣列元素值為0。但這種儲存結構並不是最簡單有效的選擇。 　　圖8.21中左邊部分給棋盤的行、列編了號，提供的擺放方法，就是問題的一個解。右邊的部分，將各行上皇后所在的列數記錄下來，用這8個數字（4, 6, 8, 2, 7, 1, 3, 5），也構成了對問題解的一種描述。

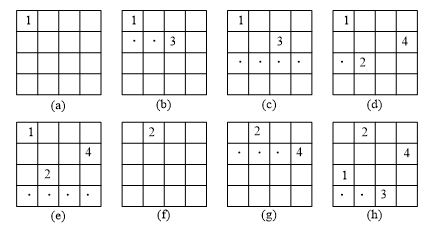
　　由此可以看出，可以定義一個一維陣列int x[N];，用x[i]的值表示第i行上皇后所在的列數，n皇后問題的解可以用（x[1], x[2], ….. x[n]）的形式描述。 　　解決了資料表示的問題，設計資料處理的方法。這裡要用回溯的策略，設計計算機對n皇后問題的求解方法。以4皇后為例，如圖8.22所示，在圖8.22(a)中，第1行第1列上放置一個皇后，圖8.22(b)中確定第2行的可能放法，在嘗試第1列、第2列由於相互攻擊而放棄之後，確定在第3列放置可以繼續，在圖8.22(c)中繼續對第3行進行考察，發現將所有4列都嘗試過了，也沒有辦法將皇后安排一個合適的位置，對第4行做任何的嘗試都沒有意義，這時產生回溯，結果是在圖8.22(d)中將第2行的皇后安排到第4列，然後第3行的暫時可以放在第2列，在圖8.22(e)中試著確定第4行的皇后，卻發現無解再次回溯，只能夠如圖8.22(f)所示將第1行的皇后放到第2列，再經圖8.22(g)、(f)之後找到4皇后問題的一個解，那就是圖8.22(g)的（2, 4, 1, 3）。

　　在圖8.23中，給出了求出4皇后問題所有解的完整過程的描述。圖中（1 * * *)對應圖8.22(a)中第1行皇后安排在第1列，其他行待定的狀態，接下來的（1 3 * *）對應了圖8.22(b)中第2行皇后安排在第3列的狀態。可以判斷出在這個狀態下，繼續嘗試並不能夠完成求解，於是發生回溯（其下方的B代表回溯），於是下一個嘗試的狀態將是（1 4 * *），……。將這樣的過程繼續下去，能夠找出4皇后問題的所有解（2 4 1 3）和（3 1 4 2），如圖8.23中兩個加網格背景的結點。 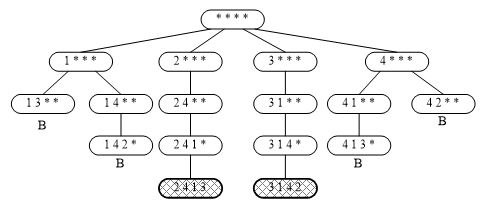圖8.23　求出4皇后問題所有解的完整過程

　　搞清楚用回溯法求解的過程後，將關注如何基於（x[1], x[2], ….. x[n]）形式的解結構，寫出讓計算機完成求解過程的程式碼。4皇后問題尚且可以在紙上畫出解，8皇后問題的可能解有8!=40320種，最終解有92種，必須要依靠計算機求解了。 　　什麼樣的解才是可行的？需要描述出任何兩個皇后可以“互相攻擊”這樣的條件： 　　（1）有兩個皇后處在同一行：解的結構（x[1], x[2], ….. x[n]）已經保證同一行不會出現兩個皇后。 　　（2）有兩個皇后處在同一列：表示為x[i]=x[k]，假如在圖8.23中出現表示為（1 1 * *）、（4 2 3 2）之類的結點，則說明有兩個皇后在同一列了。 　　（3）有兩個皇后處在同一斜線：若兩個皇后的擺放位置分別是第i行第x[i]列、第k行第x[k]列，若他們在棋盤上斜率為-1的斜線上，滿足條件i-x[i]=k-x[k]，例如（1 4 3 *）、（4 1 2 *）；若他們在棋盤上斜率為1的斜線上，滿足條件i+x[i]=k+x[k]。將這兩個式子分別變換成i-k=x[i]-x[k]和i-k=x[k]-x[i]，例如（3 4 1 *）。綜合兩種情況，兩個皇后位於同一斜線上表示為|i-k|=|x[i]-x[k]|。 　　在下面的程式實現中，place(x, k)函式用於判斷在第k行第x[k]列放置皇后，是否會與前面擺放好的皇后產生相互攻擊。只要有某行（第i行）的皇后與這個第k行的皇后處在同一列（x[i]=x[k]）或者處在同一斜線（|i-k|=|x[i]-x[k]|），則立即返回假(0)，表示不可能構成解。 　　再接下來，就是在實現問題求解的nQueens(x, n)函式中，從第1行開始，逐行逐列地考察皇后的擺放，當遇到某一行所有可能情況試過不必再深入到下一行考察時，及時回溯到上一行，接著考察。 　　程式實現中，將儲存解的陣列定義成了動態陣列。多分配一個單元，因為陣列的首元素x[0]一直空閒未用，有用的單元是x[1]到x[n]。 　　 【例8.12】 求解8皇后問題的程式

#include <stdio.h>#include <math.h>#include <malloc.h>void nQueens(int *x, int n);     /*求解n皇后問題*/int place(int *x, int k);         /*判斷是否可以在第k行第x[k]列擺放皇后*/void printSolution(int *x, int n);  /*輸出求解結果*/int main(){    int n;    int *x;                        /*存放求解結果的陣列首地址*/    scanf("%d", &n);    x=(int*)malloc(sizeof(int)*(n+1));  /*動態分配陣列空間， x[0]空閒*/    nQueens(x, n);    return 0;}/*如果一個皇后能放在第k行第x[k]列，則返回真(1)，否則返回假(0)*/int place(int *x, int k){    int i;    /*對前k-1行，逐行考察*/    for(i=1; i<k; i++)    {        /*如果前k-1行中有某行的皇后與第k行的在同一列或同一斜線，返回0*/        if((x[i]==x[k])||(fabs(x[i]-x[k])==fabs(i-k)))            return 0;    }    /*能執行下一句，說明在第k行第x[k]列擺放皇后，不會互相攻擊*/    return 1;}/*求解在n×n的棋盤上，放置n個皇后，使其不能互相攻擊*/void nQueens(int *x, int n){    int k;    k = 1;    /*k是當前行*/    x[k] = 0;  /*x[k]是當前列，進到迴圈中，立刻就會執行x[k]++，而選擇了第1列*/    while(k>0)/*當將所有可能的解嘗試完後，k將變為0，結束求解過程*/    {        x[k]++;                      /*移到下一列*/        while(x[k]<=n && !place(x, k))   /*逐列考察，找出能擺放皇后的列x[k]*/            x[k]++;        if(x[k]<=n)                   /*找到一個位置可以擺放皇后*/        {            if(k==n)                  /*是一個完整的解，輸出解*/                printSolution(x, n);            else  /*沒有完成最後一行的選擇，是部分解，轉向下一行*/            {                k++;    /*接著考察下一行*/                x[k]=0;  /*到迴圈開始執行x[k]++後，下一行將從第1列開始考察*/            }        }        else  /*對應x[k]>n的情形，這一行已經沒有再試的必要，回溯到上一行*/            k--;  /*上一行在原第x[k]列的下1列開始考察*/    }}/*輸出求解結果*/void printSolution(int *x, int n){    int i, j;    for (i = 1; i <= n; i++)    /*輸出第i行*/    {        for (j=1; j<=n; j++)        {              if (j == x[i])    /*第x[i]列輸出Q，其他列輸出*號 */                printf("Q");            else                printf("*");        }        printf("\n");    }    printf("\n");}

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33
• 34
• 35
• 36
• 37
• 38
• 39
• 40
• 41
• 42
• 43
• 44
• 45
• 46
• 47
• 48
• 49
• 50
• 51
• 52
• 53
• 54
• 55
• 56
• 57
• 58
• 59
• 60
• 61
• 62
• 63
• 64
• 65
• 66
• 67
• 68
• 69
• 70
• 71
• 72
• 73
• 74
• 75
• 76

【思考題】請從解題策略和程式中，找出何處使用了棧，是如何將棧應用於回溯過程的？