關於區塊鏈入門的一些思考

這學期選修了區塊鏈技術及其應用，瞭解了一些區塊鏈的基礎知識。現整理出一份技術總結。

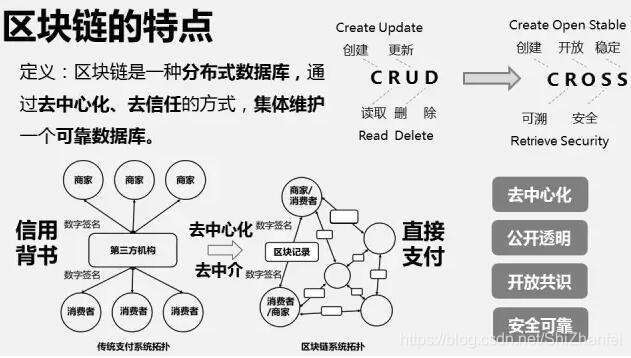
1、問題引入

在分散式系統通訊安全性中有一個著名的“拜占庭將軍問題”。該問題為：拜占庭的一些將軍出發攻打敵軍。他們每個人手握一支軍隊（方便起見設為數量相等），分佈在不同的地方紮營，彼此地位平等（即不存在相互命令）。現在的戰況為：只有進攻敵人的將軍數達到一定數量，才能戰勝敵軍，不然會戰敗。但是，由於每個將軍都分佈在不同的地方，通訊只能靠傳令兵，極為不方便。於是，每一位將軍很自然地都會想這樣一個問題：我如何信任傳令兵發來的訊息？如果他所在將軍是叛徒，告訴我明天上午九點會有五位將軍發動進攻，加上我六位，打贏妥妥的。結果明天上午我發動進攻時，發現只有我一個，那不是涼涼了，軍隊打光了要變光桿司令了。如果無法達成共識，即讓所有參與進攻的將軍都相信明天上午九點會有足夠戰勝敵人的將軍發起進攻，那進攻將難以組織。 此問題反應了分散式系統的核心問題

2、加密演算法

區塊鏈依賴網路通訊，網路通訊需要考慮資訊保安，即不能傳送資訊明文，不然被截獲就暴露了，而應傳送加密後的密文。 區塊鏈中廣泛使用的加密演算法為非對稱加密和雜湊加密。 非對稱加密的演算法原理主要基於大質數分解極為困難，會生成一把可以傳送出去的公鑰（public key）和一把只能儲存在自己手中的私鑰（private key）。用公鑰加密的訊息只能用私鑰解密，用私鑰加密的訊息只能用公鑰解密，加密和解密不是一把金鑰是此演算法“非對稱”的由來。 而雜湊加密

3、共識的達成

區塊鏈的本質是一個去中心化，高安全性，有加密的去中心化分散式系統。 區塊鏈的設計理念是任何國家的任何人都能參與到區塊鏈之中。因此想讓任何國家的任何人都達成共識，宗教信仰顯然不行，道德約束更不可能。如果嚴格審查每個人的所謂誠信值，則該系統需要一箇中心化的審查機構，該機構絕對可信，該機構稽核通過的人也絕對可以相信。這就成了中心化系統，與傳統方式（銀行等）無疑。 因此，只有基於數學的共識才能跨國界地讓所有人達成共識。 而共識，則包括非對稱加密裡涉及的數論和群論，雜湊演算法等。筆者數學知識有限，就不展開細說。

4、區塊鏈的模式(以比特幣為例）

每個區塊由上一個區塊的整體雜湊值，資訊和Nonce值組成。 資訊：以比特幣為例，資訊可以為比特幣交易、轉賬資訊 Nonce值:一個整數，使得當前區塊（上一個區塊的雜湊值+當前區塊資訊+該Nonce值）的雜湊值滿足Pow Pow（Proof of Work）:工作量證明，即雜湊值滿足某種達成很困難，驗證很簡單的特徵。在比特幣中，Pow為雜湊值最前面為60個0。滿足該條件的Nonce值想計算出一個需要海量的計算（下面會給出例項）。但是想驗證是否滿足Pow，寫一個判斷雜湊值最前面是否有60個0的函式十分容易。

區塊鏈為一個個區塊組合成鏈。新區塊包含上一個區塊（鏈末端的區塊）的雜湊值和交易資訊。接下來就是計算滿足Pow的Nonce值。計算出來後，將上一個區塊的雜湊值，資訊和該Nonce值作為新的區塊釋出，並連結到原有的區塊末端。接下來，該新區塊的雜湊值會和接下來的交易資訊一起構成下一個區塊，然後計算新的Nonce值，再產生更新的區塊。區塊鏈就是像這樣一個區塊一個區塊連結起來的。

大名鼎鼎的挖礦：在比特幣中，計算出Nonce值是會有比特幣獎勵的。所謂的挖礦，就是不停地試一個整數，當加上上一個區塊整體雜湊值加上交易資訊再加上該整數後的整體雜湊值滿足Pow（即雜湊值最前面有60個0），就叫挖到礦了。 所謂的礦就是合適的Nonce值 第一個計算出合適Nonce值會得到比特幣獎勵。然後生成新的區塊，得重新計算新的Nonce

5、一個簡單的用Java寫的挖礦小程式

package BlockChain; import java.io.*; import java.security.MessageDigest; import java.security.NoSuchAlgorithmException; import java.util.Scanner; import java.util.Date; public class Sha256Test {

public static void main(String[] args) {
	// TODO 自動生成的方法存根
	Translator t = new Translator() ;
	//System.out.println(t.getSHA256("szf"));
	final int endNum = 3 ;//Pow證明，區塊鏈為60
	String transaction = "szf" ;//交易
	int x = 1 ;//x從1開始一直算到雜湊值滿足Pow為止
	String message = transaction+x ;//交易資訊
	Date before = new Date() ;
	while(true) {
		String codedMessage = t.getSHA256(message) ;
		int zeroNumber = zeroNumber(codedMessage) ;
		if(zeroNumber==endNum){
			break ;
		}
		else {
			x++ ;
			message = transaction +x ;
		}
	}
	System.out.println("執行毫秒數為:"+(long)(new Date().getTime()-before.getTime())) ;
	System.out.println("Pow為："+endNum) ;
	System.out.println("Nonce值為:"+x) ;
	System.out.println("明文為:"+(transaction+x)) ;
	System.out.println("密文為："+t.getSHA256(message)) ;
}
//計算SHA256加密後前幾個為0
public static int zeroNumber(String message) {
	int count = 0 ;
	if(message.length()<=0) {
		System.err.println("字串為空") ;
		return 0 ;
	}
	for(int i = 0; i < message.length();i++) {
		if(message.charAt(i)=='0')count++ ;
		else break ;
	}
	return count ;
}

} class Translator{ public String getSHA256(String message) {

	MessageDigest md = null;
	String result = null ;
	try {
		md = MessageDigest.getInstance("SHA-256") ;//把加密器設定為SHA-256
		md.update(message.getBytes("UTF-8"));//把待加密message轉乘位元組陣列後上傳給加密器
		//byte[]codedMessage = md.digest() ;
		result = byte2Hex(md.digest()) ;
		
	}catch(NoSuchAlgorithmException e) {
		System.err.println("輸入的加密演算法未包含") ;
		System.exit(0);
	}catch(UnsupportedEncodingException e) {
		e.printStackTrace();
	}
	return result ;
}
//位元轉16進位制
private static String byte2Hex(byte[] bytes){
	StringBuffer stringBuffer = new StringBuffer() ;
	String temp = null ;
	for(int i = 0 ;i < bytes.length ; i++) {
		temp = Integer.toHexString(bytes[i]&0xFF) ;//通過這個操作可以把byte轉位16進位制把轉16進位制後的結果放入temp
		if(temp.length()==1) {
			//只有1位，則往StringBuffer輸入前先補個0，因為16進位制每個都是兩位，1要補成01
			stringBuffer.append("0") ;
		}
		stringBuffer.append(temp) ;
	}
	return stringBuffer.toString() ;
}

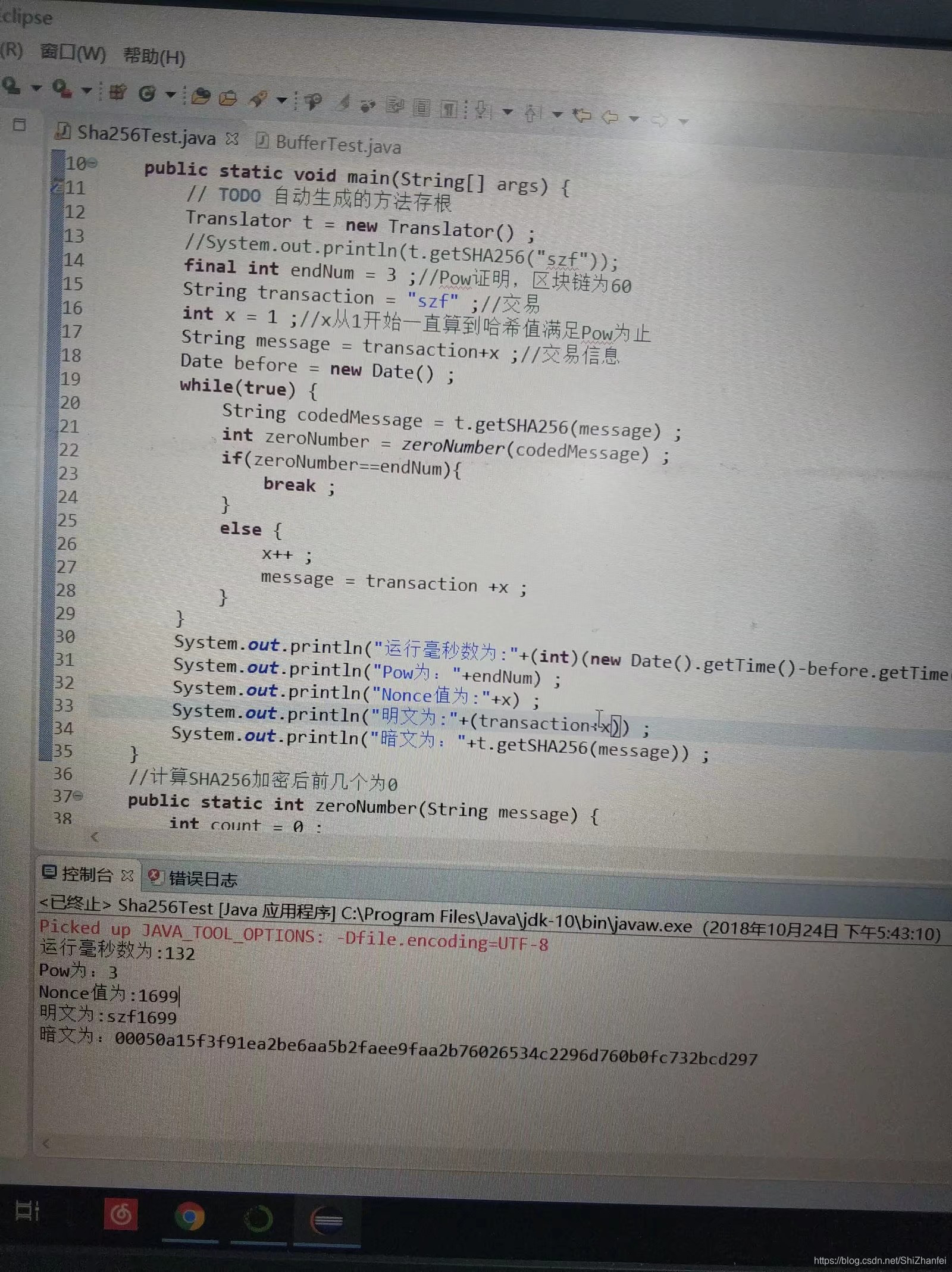
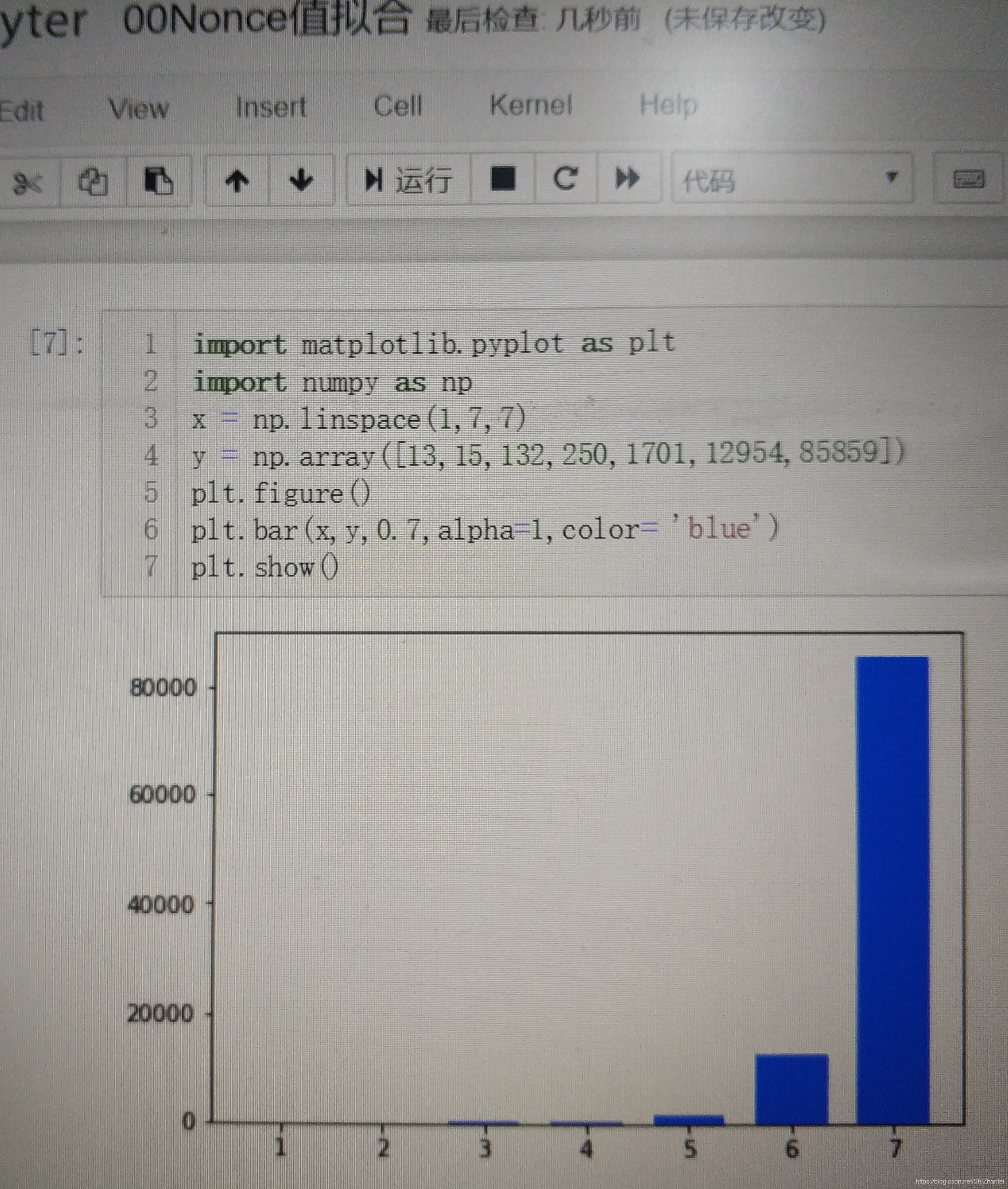
} 當Pow設為3和7（即雜湊值前有3個0，7個0的執行結果如下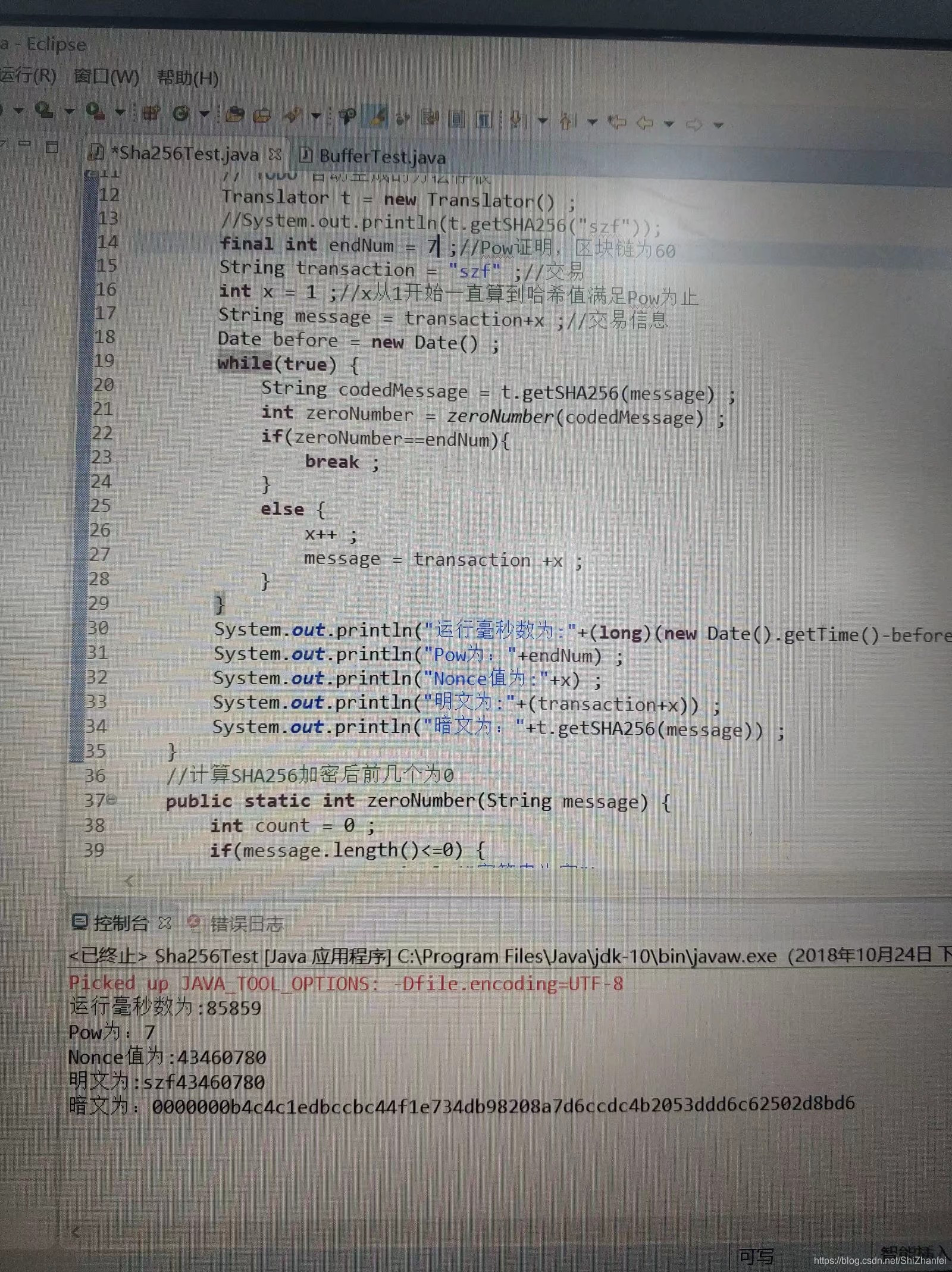） 用python畫了下柱狀圖，可以清晰看到指數爆炸的力量。當Pow為3時只有0.1秒，為7時已經暴漲到快一分半了。因此，計算一個Nonce，即挖礦是極為消耗算力的。

6、區塊鏈安全性的一些問題

1)交易篡改風險

區塊鏈的Pow十分有效，想算出一個Nonce值需要花費大量的算力資源。設計者的思想為：用高昂到超過篡改交易收益的算力消耗來儘可能避免惡意篡改交易。當篡改交易帶來的收益低於計算Nonce值的成本，這方面的惡意攻擊確實減少很多。但是，這並不能根本上規避交易篡改風險。 區塊鏈中真正用來規避交易篡改風險的方法是最長鏈原則，即認為當前網路上最長的鏈（也叫主鏈，事實上區塊鏈上除了最長的主鏈還有一些支鏈）是正確的。它的原理是：一個人幾乎不可能每次都計算出Nonce值，即這個區塊的Nonce是他計算出的，大概率下一個區塊就是別人計算出的。一個人修改了區塊的交易資訊產生一個新區塊並連結到區塊鏈上之後，別人計算出的區塊可能也包含這一交易資訊，也產生一個不同的新區塊並連結上主鏈。由於實際的交易資訊是公開的，當別的礦工計算新節點的Nonce值時，採用的是公開的正確的未經篡改的交易資訊。於是，篡改後的區塊雜湊值與別的正確資訊區塊雜湊值不一樣，正確的資訊區塊會被繼續連結並被相信為正確的（事實上這並不是絕對安全的，下面會討論）。於是正確的鏈越來越長，短鏈就成了無人問津的支鏈。因此，最長鏈原則在一般情況下可以規避交易篡改攻擊。

2）51%攻擊

這應該是區塊鏈最有名的攻擊。即如果一個人掌握了全球51%的算力，則很有可能接下來的區塊的Nonce值全部都是他計算出來的。因此，交易資訊他想怎麼寫就怎麼寫。這就是1）中提到的不是絕對安全的情況。當區塊鏈中大多數（即大於50%）的成員選擇惡意欺騙攻擊時，最長鏈原則也無法保證區塊的安全。所幸目前幾個較大型的礦池還沒達到這樣的算力，因此暫時較為安全。

3) 雙花攻擊

所謂的”雙花“，就是同一筆錢花了兩次。這在中心化系統中可以有效規避（如支付寶想雙花很難），但在分散式系統中，由於網路延遲以及Pow的關係，雙花攻擊風險較大。比如攻擊者錢包裡有1個比特幣，他在A地花了1個比特幣，A地驗證他錢包裡確實有1個比特幣，於是交易成功被記入區塊等待礦工挖礦並鏈上主鏈。但緊接著，攻擊者在B地又花了1個比特幣，此時B地網路還未接收到攻擊者在A地花1個比特幣的區塊，驗證他錢包有1個比特幣，然後交易通過。也就是說，1個比特幣花了兩次。 這是當前區塊鏈最嚴重最難以規避的問題。區塊鏈賬戶設計時是匿名的，賬戶地址僅僅是一把私鑰，就算查到賬戶也難以追查。（支付寶繫結銀行卡手機號就不會有這個問題）。具體解決方法筆者剛剛接觸區塊鏈也不是很清楚。

7、個人對區塊鏈技術的看法

在我看來，區塊鏈是一個高安全性，無中心的自由的技術。去中心化理論上連中心發動攻擊都規避了，絕對安全。並且由於分散式難以被攻擊（攻擊者可以炸燬支付寶總部但面對區塊鏈無從下手）。 但是，除了發幣之外，我覺得區塊鏈技術似乎看不出什麼太大的用處（可能是我才大二上水平太低。。） 我難以想象銀行會攻擊自己自我毀滅。規避中心發動攻擊的功能有些雞肋。 至於難以被攻擊的特性，炸燬支付寶總部這種事同樣不可能被髮生。 而區塊鏈大量算力資源的白白浪費的問題是很明顯的。大量算力被浪費在反覆進行SHA256雜湊運算上，如果不是第一個算出Nonce值的，則這些算力就真的白白浪費了。我不覺得目前的算力可以這麼揮霍，科學計算，人工智慧，大資料，以及大量其他領域迫切需要算力資源。哪怕是浪費算力，可能也比浪費在不停進行SHA256雜湊運算上強。 並且，大量算力的浪費是區塊鏈不可避免的。現代資訊理論中有這樣的理論，要想在去中心化分散式系統中達成共識，必須釋放大量能源來降低資訊熵（大概就是想要達成共識大量浪費資源來做工作量證明是不可避免的）。因此，算力的大量問題似乎根本上就無法避免。 總而言之，對區塊鏈技術，我持觀望態度。

電子科技大學 機械與電氣工程學院 智慧電網資訊工程本科大二 施展飛 2018.11.13