本文是由《Nonlinearly Activated Neural Network for Solving Time-Varying Complex Sylvester Equation》做的總結

一般的時不變西爾維斯特方程定義在複數域內，Bartels-Stewart演算法及其擴充套件是可以解決靜態西爾維斯特方程，並且廣泛用於O（n3）時間複雜度。當應用於求解時變Sylvester方程時，計算負擔隨著取樣週期的減少而增加，並且不能滿足連續的實時計算要求。

對於在實數域中定義的一般Sylvester方程問題的特殊情況，基於梯度的神經網路可以實時解決時變（實值）西爾維斯特方程，它利用誤差矩陣的範數作為效能指標，並設計一個神經網路沿著梯度下降的方向使誤差範數在時不變

的情況下隨著時間收斂為零。但是總是存在著誤差。對於時變情況，由於缺少時變引數的速度補償，即使在無限長的時間之後誤差範數也可能不會收斂到零。

而張則提出的ZNN(一種新型的迴圈神經網路）可以收斂到理想值，成功地解決了傳統的基於梯度的遞迴神經網路在用於求解時變實值Sylvester方程時遇到的估計誤差問題。 與基於梯度的遞迴神經網路相比，ZNN的一個突出優勢在於，當時間變為無窮大時，估計誤差減小到零。

復值神經網路的擴充套件現有的實值ZNN，用於求解時變實值Sylvester方程到複數域中的對應方程。由於復值神經網路能夠直接處理複數域中定義的問題，以及ZNN在解決實值時間變化問題方面取得的巨大成功，我們在本文中探討了復值ZNN用於求解復值時變Sylvester方程。 並利用所提出的非線性復值啟用函式證明了神經網路的全域性收斂性。SBP函式（嵌入在複數值非線性啟用函式中）證明ZNN能夠在有限時間

收斂，增強了線上處理能力。收斂時間的上限也被求出。 進行模擬不同引數和啟用函式以評估和比較神經網路的效能與理論分析和數值模擬均驗證了該方法的有效性。

復值的神經網路比實值的神經網路應用範圍更廣。為了保證神經網路的全域性收斂，僅考慮線性啟用函式。而一些較好設計的非線性啟用函式能手加速實值ZNN的收斂，也有利於線上處理。這激發了我們探索是否可以找到某些非線性復值啟用函式，而不是簡單地使用線性啟用函式來加速神經網路的收斂，因為在實數域中定義的非線性啟用的ZNN通常會都是這樣的，並且仍然保證神經網路的全域性收斂。本文找到兩種啟用函式去求解復值時變Sylvester方程，保證了復值ZNN的全域性收斂性。

復值時變Sylvester方程和ZNN設計過程

復值時變西爾維斯特方程如下：

A（t），B（t）和C（t）是已知復值時變矩陣，X（t）是適當大小的未知矩陣。

為了討論復值時變西爾維斯特方程（1），提出了兩種假設。

假設1：時變矩陣A（t），B（t）和C（t）隨時間t連續可微，A（t），B（t）和C（t）及其時間導數 是統一有界的。

假設2：矩陣A（t）和-B（t）沒有共同的特徵值。

可微指的是: 函式在某點存在導數，即光滑連續。

在介紹用於求解復值西爾維斯特方程的復值ZNN之前，我們首先重新討論實值ZNN的設計方法，以求解實值Sylvester方程。

用ZNN求解實值時變西爾維斯特方程這是（1）的特殊情況，其中A（t），B（t）和C（t）是實值矩陣，但可能會對問題（1）產生靈感。

備註1：ZNN（4）中X（t）的動力學是隱式微分方程而不是顯式微分方程。

如果啟用函式是奇數且單調遞增，用於求解實值時變西爾維斯特方程時，實值ZNN能夠保證全域性收斂。由於非線性啟用函式能夠加速收斂，這表明非線性復值啟用在加速復值ZNN收斂方面的可能性，並激勵我們的研究將實值ZNN中使用的現有非線性啟用函式擴充套件到復值ZNN。然而，將實數域中定義的非線性啟用函式擴充套件到複數域並但仍然保證神經動力學的全域性收斂並不是直截了當的。這也可能是啟用函式僅被選擇為線性的原因。

 

提出的模型和復值非線性啟用函式

由求解實值西爾維斯特方程的實值ZNN（4）推出如下的求解復值西爾維斯特方程（1）的復值ZNN：

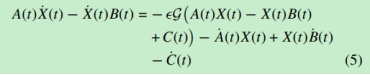
G(·)與公式實值ZNN（4）中的H(·)相等 ，它是復值啟用函式。

備註2：當我們選擇B（t）= 0和C（t）= -I時，時變復值Sylvester方程問題（1）簡化為復值矩陣求逆問題（I是單位矩陣） ，它可以通過神經網路（5）計算復值方陣A（t）的倒數。

備註3：大的E值能夠加速收斂，但在魯棒性方面則會放大噪聲，使系統對噪聲敏感。所以取適當的E值，本文E=1.

由（5）推出（6）

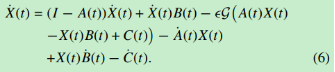
系統中使用導數塊可以不需要實現神經網路時根據（6）中的X（t）求解X’（t）,相反，X（t）可以使用類比電路求解。

備註4：正如在比例 - 積分 - 微分控制器的實際實現中經常做的那樣，最好在訊號進入微分塊之前，通過圖1中的低通濾波器來降低導數塊對噪聲的靈敏度。

我們以兩種方式將實值啟用函式擴充套件到複數域：

。表示逐元素乘；為了能夠相容實值ZNN，F（·）是奇數且單調遞增。輸入實值時，方法1和2都退化為實值對映F（·），說明方法1和2能在實值ZNN使用啟用函式；如果F（·）十非線性對映，則方法1和2的啟用函式的值不同，線性則相同。

當F（·）被選擇為具有F（X）= X的線性函式時，兩種型別是相同的。 當輸入一個實值矩陣時，兩種G1/G2啟用函式都退化為實值對映F（·）。如F(0)=0,G1(0)=0;G2(0)=0。一般而言，如果選擇F（·）作為非線性對映，則型別I啟用函式和型別II啟用函式的值不同。

 

備註8：（21）中定義的符號雙功率啟用函式是強非線性函式。 當r接近1時，符號雙功率啟用函式接近線性函式y = x。 此外，符號雙冪函式的特性是，對於相同的輸入，r =η和r =1/η（η> 0）的兩個不同符號雙冪函式的輸出分別總是相同的

 

定理1：給定滿足假設1和2的時變矩陣A（t），B（t）和C（t），如果型別I啟用函式G1（·）[如（7）中定義]具有奇數 並且使用單調遞增函式F（·），則從任何初始狀態X0開始的復值ZNN（5）的狀態矩陣X（t）總是收斂到時變複數的時變理論解。 西爾維斯特公式（1）

定理2：給定滿足假設1和2的時變矩陣A（t），B（t）和C（t），如果型別II啟用函式G2（·）[如（8）中定義]， 使用奇數和單調遞增函式F（·），則從任何初始狀態X0開始的復值ZNN（5）的狀態矩陣X（t）總是收斂到時間的時變理論解。 變復值Sylvester方程（1）

定理3：給定滿足假設1和2的時變矩陣A（t），B（t）和C（t），如果在（7）中定義的型別I（或型別II）啟用函式G1（·）[ 或者（8）中定義的G2（·）具有在（21）中為r> 0定義的符號雙冪函式F（·），並且r！= 1，然後使用狀態矩陣X（t） 從任何初始狀態X0開始的復值ZNN（5）總是收斂於時變復值Sylvester方程（1）在有限時間內的時變理  論解。

 

實值ZNN可被視為復值的特殊例子，由於它是無限時長收斂，減少了ZNN在實時方面的應用。

 

相對比不同的函式F（·）的模擬和SBP函式選擇不同r的結果

---

注：

1.隱式微分方程和顯示微分方程的比較

ZNN（4）中X（t）的動力學是隱式微分方程而不是顯式的。這種隱含的ZNN可以重新表述為具有區域性神經動力學的互聯絡統，並且可以有效地解決。可參考論文《Design and analysis of a general recurrent neural network model for time-varying matrix inversion》、《Zhang Neural Networks and Neural-Dynamic Method》、《A recurrent neural network for solving
Sylvester equation with time-varying coefficients》

顯示求解是對時間進行差分，不存在迭代（穩定性）和收斂問題，最小時間步取決於最小單元的尺寸。過多和過小的時間步往往導致求解時間非常漫長，但總能給出一個計算結果。飲食求解與時間無關，採用的是牛頓迭代法（線性問題就直接求解線性代數方程組），因此存在一個迭代收斂問題，不收斂就得不到結果。

顯示解釋函式的形式，隱式解釋方程的形式。

2.當我們選擇B（t）= 0和C（t）= -I（I是適當大小的單位矩陣）時，時變復值Sylvester方程問題（1）簡化為復值矩陣求逆問題 並且可以通過神經網路（5）計算復值方陣A（t）的倒數。

3、值越大，收斂速度越快，但是在魯棒性方面，值越大，通常會放大噪音並使系統對噪音敏感。所以要選擇一個合適的值。

4、為啥一定要使用奇單調遞增的啟用函式，才能夠收斂到理論解呢？

李雅普洛夫穩定性理論的要求，就是隻有滿足這個條件 網路才會收斂，必須保證構造的那個李雅普洛夫函式v=e^2的導數，在e大於零的時候為負值，導數為負值就會使V的值下降（或者說減少），如果不是單增的話，它有可能減少到小於零的情況，這樣不能保證v會減少，反而增加就是說誤差反而再增大。