導讀

本文的結構安排如下目錄。首先介紹了HMM的基本定義；然後引出HMM的3個基本問題中；在前兩個環節中通過一個淺顯易懂的案例幫助理解；其次是針對3個問題中用到演算法的理論介紹；最後介紹了預測天氣的HMM經典案例，並附有python程式碼。

目錄

案例和程式碼

參考文獻

隱馬爾可夫模型的定義

隱馬爾可夫模型是關於時序的概率模型，描述由一個隱藏的馬爾科夫鏈隨機生成不可觀測的狀態隨機序列，再由各個狀態生成一個觀測而產生觀測隨機序列的過程。隱藏的馬爾科夫鏈隨機生成的狀態序列，成為狀態序列（state sequence）；每個狀態生成一個觀測，而由此產生的觀測的隨機序列，成為觀測序列

（observation sequence）。序列的每一個位置又可以看作是一個時刻。隱馬爾可夫模型由初始概率分佈、狀態轉移概率分佈以及觀測概率分佈確定。

HMM的形式定義

對於HMM模型，首先我們假設Q是所有可能的隱藏狀態的集合，V是所有可能的觀測狀態的集合，即：

其中，N是可能的隱藏狀態數，M是所有的可能的觀察狀態數。

I 是長度為T的狀態序列， O是對應的觀察序列

A是狀態轉移概率矩陣：

其中，

是在時刻 t 處於狀態  的條件下載時刻 t+1 轉移到狀態的概率。 

B是觀測概率矩陣：

其中，

是在時刻 t 處於狀態條件下生成觀測的概率。

是初始狀態概率向量：

其中，

是時刻 t=1處於狀態  的概率。

隱馬爾可夫模型模型，由隱藏狀態初始概率分佈 , 狀態轉移概率矩陣A和觀測狀態概率矩陣B決定。和A決定狀態序列，B決定觀測序列。因此，隱馬爾可夫模型  可以用三元符號表示，即

直觀理解HMM的各個狀態

假設我手裡有三個不同的骰子。第一個骰子是我們平常見的骰子（稱這個骰子為D6），6個面，每個面（1，2，3，4，5，6）出現的概率是1/6。第二個骰子是個四面體（稱這個骰子為D4），每個面（1，2，3，4）出現的概率是1/4。第三個骰子有八個面（稱這個骰子為D8），每個面（1，2，3，4，5，6，7，8）出現的概率是1/8。

假設我們開始擲骰子，我們先從三個骰子裡挑一個，挑到每一個骰子的概率都是1/3。然後我們擲骰子，得到一個數字，1，2，3，4，5，6，7，8中的一個。不停的重複上述過程，我們會得到一串數字，每個數字都是1，2，3，4，5，6，7，8中的一個。例如我們可能得到這麼一串數字（擲骰子10次）：1 6 3 5 2 7 3 5 2 4

這串數字叫做可見狀態鏈。但是在隱馬爾可夫模型中，我們不僅僅有這麼一串可見狀態鏈，還有一串隱含狀態鏈。在這個例子裡，這串隱含狀態鏈就是你用的骰子的序列。比如，隱含狀態鏈有可能是：D6 D8 D8 D6 D4 D8 D6 D6 D4 D8

一般來說，HMM中說到的馬爾可夫鏈其實是指隱含狀態鏈，因為隱含狀態（骰子）之間存在轉換概率（transition probability）。在我們這個例子裡，D6的下一個狀態是D4，D6，D8的概率都是1/3。D4，D8的下一個狀態是D4，D6，D8的轉換概率也都一樣是1/3。這樣設定是為了最開始容易說清楚，但是我們其實是可以隨意設定轉換概率的。比如，我們可以這樣定義，D6後面不能接D4，D6後面是D6的概率是0.9，是D8的概率是0.1。這樣就是一個新的HMM。

同樣的，儘管可見狀態之間沒有轉換概率，但是隱含狀態和可見狀態之間有一個概率叫做輸出概率（emission probability）。就我們的例子來說，六面骰（D6）產生1的輸出概率是1/6。產生2，3，4，5，6的概率也都是1/6。我們同樣可以對輸出概率進行其他定義。比如，我有一個被賭場動過手腳的六面骰子，擲出來是1的概率更大，是1/2，擲出來是2，3，4，5，6的概率是1/10。

 隱含狀態轉換關係示意圖：

這裡，

轉換概率即為狀態轉移矩陣A：

這裡我們假設D4，D6，D8後面跟隨任意一種篩子的概率相同，都是1/3。（實際問題中可以定義為不同概率，如D4後面出現D4，D6，D8的概率分別為1/,6，2/6，3/6）

D4	D6	D8
D4	1/3	1/3	1/3
D6	1/3	1/3	1/3
D8	1/3	1/3	1/3

輸出概率即為觀測概率矩陣B：

1	2	3	4	5	6	7	8
D4	1/4	1/4	1/4	1/4	0	0	0	0
D6	1/6	1/6	1/6	1/6	1/6	1/6	0	0
D8	1/8	1/8	1/8	1/8	1/8	1/8	1/8	1/8

初始狀態概率向量：

D4	D6	D8
1/3	1/3	1/3

隱馬爾可夫模型的3個基本問題

1.  概率計算問題：評估觀察序列概率。即給定模型λ=(A,B,)和觀測序列O={o1,o2,...oT}，計算在模型 λ 下觀測序列O出現的概率P(O|λ)。這個問題的求解需要用到前向後向演算法，是三個基本問題中最簡單的演算法。
2. 預測問題，也稱為解碼問題。即給定模型λ=(A,B,)和觀測序列O={o1,o2,...oT}，求給定觀測序列條件概率P(I |O)下，最可能出現的對應的狀態序列 I =( ,,...)。即給定觀測序列，求最有可能的對應的狀態序列。這個問題的求解需要用到基於動態規劃的維特比演算法，這個問題是HMM模型三個問題中複雜度居中的演算法。
3. 模型引數學習問題。即給定觀測序列O={o1,o2,...oT}，估計模型λ=(A,B,)的引數，使該模型下觀測序列的條件概率P(O | λ)最大。這個問題的求解需要用到基於EM演算法的鮑姆-韋爾奇演算法，是HMM模型三個問題中最複雜的。

簡單的概率計算例子

在進行上面3個問題用到的方法講解之前，也講一個簡單的例子。以上文的骰子為例，我們已知骰子有幾種，每種骰子是什麼，每次擲的都是什麼骰子，根據擲骰子的結果，求產生這個結果的概率。

解法無非就是概率相乘：

1. 概率計算問題的求解

概率計算問題用擲骰子為例，就是如果你在賭場中總是輸錢，那麼你可以產生懷疑：是不是賭場的骰子有貓膩？現在已知一個觀察到的骰子序列O，依據已知的模型引數（A，B，），計算出現這個序列的概率，看是否和你在賭場擲的實際概率相符，如果相差太大，那麼你的骰子很大可能有問題了。 比如說你懷疑自己的六面骰被賭場動過手腳了，有可能被換成另一種六面骰，這種六面骰擲出來是1的概率更大，是1/2，擲出來是2，3，4，5，6的概率是1/10。你怎麼辦麼？

答案很簡單，算一算正常的三個骰子擲出一段序列的概率，再算一算不正常的六面骰和另外兩個正常骰子擲出這段序列的概率。如果前者比後者小，你就要小心了。

首先，如果我們只擲一次骰子：

看到結果為1。產生這個結果的總概率可以按照如下計算，總概率為0.18：

把這個情況拓展，我們擲兩次骰子：

繼續拓展，我們擲三次骰子：

看到結果為1，6，3.產生這個結果的總概率可以按照如下計算，總概率為0.03：

同樣的，我們一步一步的算，有多長算多長，再長的馬爾可夫鏈總能算出來的。用同樣的方法，也可以算出不正常的六面骰和另外兩個正常骰子擲出這段序列的概率，然後我們比較一下這兩個概率大小，就能知道你的骰子是不是被人換了。

解決這個問題的演算法叫做前向後向演算法（forward algorithm）。 

2. 預測問題的求解

預測問題也就是解最大似然路徑問題。 舉例來說，已知我有三個骰子：六面骰，四面骰，八面骰。並且知道我擲了十次的結果（1 6 3 5 2 7 3 5 2 4），但我不知道每次用了那種骰子，我想知道最有可能的骰子序列。

其實最簡單而暴力的方法就是窮舉所有可能的骰子序列，然後依照簡單的概率計算例子的解法把每個序列對應的概率算出來。然後我們從裡面把對應最大概率的序列挑出來就行了。如果馬爾可夫鏈不長，當然可行。如果長的話，窮舉的數量太大，就很難完成了。 

另外一種很有名的演算法叫做Viterbi algorithm. 要理解這個演算法，我們先看幾個簡單的列子。 
首先，如果我們只擲一次骰子：

看到結果為1.對應的最大概率骰子序列就是D4，因為D4產生1的概率是1/4，高於1/6和1/8. 
把這個情況拓展，我們擲兩次骰子：

結果為1，6.這時問題變得複雜起來，我們要計算三個值，分別是第二個骰子是D6，D4，D8的最大概率。顯然，要取到最大概率，第一個骰子必須為D4。這時，第二個骰子取到D6的最大概率是 

同樣的，我們可以計算第二個骰子是D4或D8時的最大概率。我們發現，第二個骰子取到D6的概率最大。而使這個概率最大時，第一個骰子為D4。所以最大概率骰子序列就是D4 D6。 
繼續拓展，我們擲三次骰子：

 同樣，我們計算第三個骰子分別是D6，D4，D8的最大概率。我們再次發現，要取到最大概率，第二個骰子必須為D6。這時，第三個骰子取到D4的最大概率是：

同上，我們可以計算第三個骰子是D6或D8時的最大概率。我們發現，第三個骰子取到D4的概率最大。而使這個概率最大時，第二個骰子為D6，第一個骰子為D4。所以最大概率骰子序列就是D4 D6 D4。

寫到這裡，大家應該看出點規律了。既然擲骰子一二三次可以算，擲多少次都可以以此類推。我們發現，我們要求最大概率骰子序列時要做這麼幾件事情。首先，不管序列多長，要從序列長度為1算起，算序列長度為1時取到每個骰子的最大概率。然後，逐漸增加長度，每增加一次長度，重新算一遍在這個長度下最後一個位置取到每個骰子的最大概率。因為上一個長度下的取到每個骰子的最大概率都算過了。當我們算到最後一位時，就知道最後一位是哪個骰子的概率最大了。然後，我們要把對應這個最大概率的序列從後往前推出來。

這就是基於動態規劃的維特比演算法的求解最大可能隱藏序列的思路。

前向後向演算法

前向後向演算法是前向演算法和後向演算法的統稱，這兩個演算法都可以用來求HMM觀測序列的概率。我們先來看看前向演算法是如何求解這個問題的。

前向演算法本質上屬於動態規劃的演算法，也就是我們要通過找到區域性狀態遞推的公式，這樣一步步的從子問題的最優解拓展到整個問題的最優解。

在前向演算法中，通過定義“前向概率”來定義動態規劃的這個區域性狀態。什麼是前向概率呢, 其實定義很簡單：定義時刻 t 時隱藏狀態為qi, 觀測狀態的序列為o1,o2,...ot 的概率為前向概率。記為：

前向傳播演算法流程

輸入：隱馬爾可夫模型  ，觀測序列 O；

輸出：觀測序列概率 P（O|）。

1）初值

2） 遞推。對於 t =1,2,...T-1,

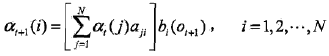
3) 終止

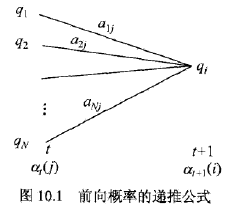
前向傳播演算法，步驟1）初始化前向概率，是初始時刻的狀態和觀測O1的聯合概率。步驟2）是前向概率的遞推公式，計算到時刻 t+1部分觀測序列為且在時刻 t+1 處於狀態q1的前向概率，如下圖10.1所示。在步驟2）的方括號裡，既然是到時刻 t 觀測到並在時刻 t 處於狀態的前向概率，那麼乘積就是時刻 t 觀測到並在時刻 t 處於狀態  而在時刻 t+1 到達狀態 的聯合概率。對這個乘積在時刻 t 的所有可能的 N 個狀態求和，其結果就是到時刻 t 觀測為並在時刻 t+1 處於狀態 的聯合概率。方括號裡的值與觀測概率的乘積恰好是到時刻 t+1 觀測到 並在時刻 t+1 處於狀態的前向概率。步驟3）給出了的計算公式。

因為

所以

                                                                 

注：關於後向演算法請參看部落格最後的參考文獻 。

維特比演算法概述

維特比演算法實際是用動態規劃解隱馬爾可夫模型預測問題，即用動態規劃（dynamic programming）求概率最大路徑（最優路徑）。這時一條路徑對應著一個狀態序列。

既然是動態規劃演算法，那麼就需要找到合適的區域性狀態，以及區域性狀態的遞推公式。在HMM中，維特比演算法定義了兩個區域性狀態用於遞推。

第一個區域性狀態是在時刻tt隱藏狀態為ii所有可能的狀態轉移路徑i1,i2,...it中的概率最大值。記為:

由定義可得變數 的遞推公式：

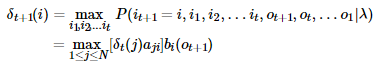
第二個區域性狀態由第一個區域性狀態遞推得到。定義在時刻 t 隱藏狀態為 i 的所有單個狀態轉移路徑（i1,i2,...,it−1,i）中概率最大的轉移路徑中第 t-1個節點的隱藏狀態為，其遞推表示式為：

有了這兩個區域性狀態，我們就可以從時刻0一直遞推到時刻T，然後利用記錄的前一個最可能的狀態節點回溯，直到找到最優的隱藏狀態序列。

維特比演算法流程：

輸入：模型和觀測：

輸出：最優路徑。

1)初始化

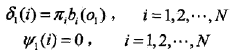
2）遞推。對 t =2,3,...,T

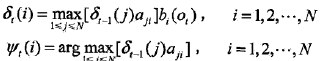
3）終止

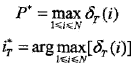
4）最優路徑回溯。對 t = T-1,T-2,...,1

求得最優路徑。

鮑姆-韋爾奇演算法

鮑姆-韋爾奇演算法原理既然使用的就是EM演算法的原理，那麼我們需要在E步求出聯合分佈P(O,I|λ)基於條件概率P(I|O,)的期望，其中為當前的模型引數，然後再M步最大化這個期望，得到更新的模型引數λ。接著不停的進行EM迭代，直到模型引數的值收斂為止。

首先來看看E步，當前模型引數為, 聯合分佈P(O,I|λ)基於條件概率P(I|O,)的期望表示式為：

 在M步，我們極大化上式，然後得到更新後的模型引數如下：

通過不斷的E步和M步的迭代，直到收斂。

演算法流程：

這裡我們概括總結下鮑姆-韋爾奇演算法的流程。

輸入： D個觀測序列樣本{(O1),(O2),...(OD)}

輸出：HMM模型引數

1)隨機初始化所有的πi,aij,bj(k)

2) 對於每個樣本d=1,2,...D用前向後向演算法計算γ(d)t(i)，ξ(d)t(i,j),t=1,2...T

3)  更新模型引數：

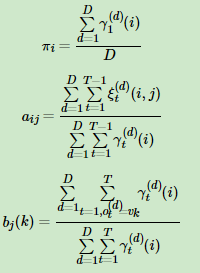
 4) 如果πi,aij,bj(k)的值已經收斂，則演算法結束，否則回到第2）步繼續迭代。

注：求HMM引數的演算法有點難度，暫時沒有完全理解。先放一個流程。有需要的可以最後參考文獻部分。

案例和程式碼

任何一個HMM問題都可以通過下列五元組描述

1.     :param obs:觀測序列
2.     :param states:隱狀態
3.     :param start_p:初始概率（隱狀態）
4.     :param trans_p:轉移概率（隱狀態）
5.     :param emit_p: 發射概率 （隱狀態表現為顯狀態的概率）

預測隱藏狀態問題：求解最可能的天氣

背景：一個東京的朋友每天根據天氣{下雨，天晴}決定當天的活動{公園散步,購物,清理房間}中的一種，我每天只能在twitter上看到她發的推“啊，我前天公園散步、昨天購物、今天清理房間了！”，那麼我可以根據她發的推特推斷東京這三天的天氣。在這個例子裡，顯狀態是活動，隱狀態是天氣。

這個例子用HMM來描述：

states = ('Rainy', 'Sunny')
 
observations = ('walk', 'shop', 'clean')
 
start_probability = {'Rainy': 0.6, 'Sunny': 0.4}
 
transition_probability = {
    'Rainy' : {'Rainy': 0.7, 'Sunny': 0.3},
    'Sunny' : {'Rainy': 0.4, 'Sunny': 0.6},
    }
 
emission_probability = {
    'Rainy' : {'walk': 0.1, 'shop': 0.4, 'clean': 0.5},
    'Sunny' : {'walk': 0.6, 'shop': 0.3, 'clean': 0.1},
}

求解最可能的隱狀態序列是HMM的三個典型問題之一，通常用維特比演算法解決。維特比演算法就是求解HMM上的最短路徑（log(prob)，也即是最大概率）的演算法。

稍微用中文講講思路，很明顯，第一天天晴還是下雨可以算出來：

1. 定義V[時間][今天天氣] = 概率，注意今天天氣指的是，前幾天的天氣都確定下來了（概率最大）今天天氣是X的概率，這裡的概率就是一個累乘的概率了。
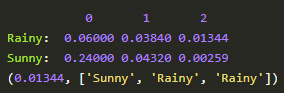
2. 因為第一天我的朋友去散步了，所以第一天下雨的概率V[第一天][下雨] = 初始概率[下雨] * 發射概率[下雨][散步] = 0.6 * 0.1 = 0.06，同理可得V[第一天][天晴] = 0.24 。從直覺上來看，因為第一天朋友出門了，她一般喜歡在天晴的時候散步，所以第一天天晴的概率比較大，數字與直覺統一了。
3. 從第二天開始，對於每種天氣Y，都有前一天天氣是X的概率 * X轉移到Y的概率 * Y天氣下朋友進行這天這種活動的概率。因為前一天天氣X有兩種可能，所以Y的概率有兩個，選取其中較大一個作為V[第二天][天氣Y]的概率，同時將今天的天氣加入到結果序列中
4. 比較V[最後一天][下雨]和[最後一天][天晴]的概率，找出較大的哪一個對應的序列，就是最終結果。

這個例子的Python程式碼：

# -*- coding: utf-8 -*-
states = ('Rainy', 'Sunny')

observations = ('walk', 'shop', 'clean')

start_probability = {'Rainy': 0.6, 'Sunny': 0.4}

transition_probability = {
    'Rainy': {'Rainy': 0.7, 'Sunny': 0.3},
    'Sunny': {'Rainy': 0.4, 'Sunny': 0.6},
}

emission_probability = {
    'Rainy': {'walk': 0.1, 'shop': 0.4, 'clean': 0.5},
    'Sunny': {'walk': 0.6, 'shop': 0.3, 'clean': 0.1},
}

# 列印路徑概率表
def print_dptable(V):
    print("    ")
    for i in range(len(V)):
        print("%7d" % i)

    for y in V[0].keys():
        print("%.5s: " % y)
        for t in range(len(V)):
            print("%.7s" % ("%f" % V[t][y]))
        print()


def viterbi(obs, states, start_p, trans_p, emit_p):
    """
    :param obs:觀測序列
    :param states:隱狀態
    :param start_p:初始概率（隱狀態）
    :param trans_p:轉移概率（隱狀態）
    :param emit_p: 發射概率 （隱狀態表現為顯狀態的概率）
    :return:
    """
    # 路徑概率表 V[時間][隱狀態] = 概率
    V = [{}]
    # 一箇中間變數，代表當前狀態是哪個隱狀態
    path = {}

    # 初始化初始狀態 (t == 0)
    for y in states:
        V[0][y] = start_p[y] * emit_p[y][obs[0]]
        path[y] = [y]

    # 對 t > 0 跑一遍維特比演算法
    for t in range(1, len(obs)):
        V.append({})
        newpath = {}

        for y in states:
            # 概率 隱狀態 =    前狀態是y0的概率 * y0轉移到y的概率 * y表現為當前狀態的概率
            (prob, state) = max([(V[t - 1][y0] * trans_p[y0][y] * emit_p[y][obs[t]], y0) for y0 in states])
            # 記錄最大概率
            V[t][y] = prob
            # 記錄路徑
            newpath[y] = path[state] + [y]

        # 不需要保留舊路徑
        path = newpath

    print_dptable(V)
    (prob, state) = max([(V[len(obs) - 1][y], y) for y in states])
    return (prob, path[state])

def example():
    return viterbi(observations,
                   states,
                   start_probability,
                   transition_probability,
                   emission_probability)
if __name__=='__main__':
    print(example())

輸出：

參考文獻

李航，《統計學習方法》，

電子版百度雲：連結：https://pan.baidu.com/s/1jC2sGVlT0GwTrhHewUbinA 
提取碼：hetz